Say we need to solve a recurrence of the form :
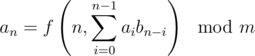
Here, f is an arbitrary function which can be computed in O(1). An example of such a problem is 553E - Kyoya and Train. The tutorial gives a solution in 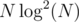 .
.
I recently saw a similar problem in codechef may long SERSUM, where I used another technique which I had thought of when I saw the prior problem. In this post I explain this very simple and intuitive sqrt decomposition solution, running in 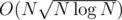 which works in almost the same time as
which works in almost the same time as 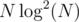 solution because of a very low constant. Here goes:
solution because of a very low constant. Here goes:
Let us divide into blocks of size say K, giving us a total of ⌈ N / K⌉ blocks. Block t consists of [(t - 1)K, tK - 1]
Let 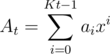 .
.
Let Ct = AtB.
When processing the block t + 1 we assume that we know Ct, which is computed when block t has been completely processed. So, we compute Ct a total of  times using FFT in time
times using FFT in time 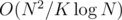 .
.
Consider some n between [tK, (t + 1)K - 1]. Then, 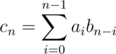

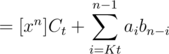 .
.
Clearly, the right part can be calculated in O(K), and we have an extra time of O(NK) because of this part.
Overall complexity =  , which is minimized taking
, which is minimized taking 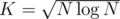 , and overall complexity is
, and overall complexity is 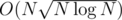 .
.
An optimization:
Note that the right part can be computed with only one mod operation if we use m2 = m * m, and keep subtracting m2 when the total sum exceeds it. Eventually we take total sum modulo m. This is a very common technique, which we use in matrix multiplication as well.
This means that we should use a block size even greater than 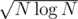 for better results, because of a huge constant difference in the two parts. (Computing Ct using FFT, and computing the remaining sum in O(k) using brute force iteration with the optimization above.) Just as an example, for N = 105, and m = 109 + 7 (which is a bad mod value for FFT problems), the best performance comes when you take K ≈ 6 × 103. For this input size it runs in about 2 seconds, which is pretty good.
for better results, because of a huge constant difference in the two parts. (Computing Ct using FFT, and computing the remaining sum in O(k) using brute force iteration with the optimization above.) Just as an example, for N = 105, and m = 109 + 7 (which is a bad mod value for FFT problems), the best performance comes when you take K ≈ 6 × 103. For this input size it runs in about 2 seconds, which is pretty good.





