Hello, Codeforces!
I think many of you know about Mo's algorithm. For those, who don't know, please read this blog.
Here, I consider an alternative (and faster) approach of sorting queries in Mo's algorithm.
Table of contents
Canonical version of the algorithm
The canonical version of this algorithm has 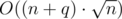 time complexity if insertions and deletions work in O(1).
time complexity if insertions and deletions work in O(1).
Usually, the two comparators for query sorting are used. The slowest one:
struct Query {
int l, r, idx;
inline pair<int, int> toPair() const {
return make_pair(l / block, r);
}
};
inline bool operator<(const Query &a, const Query &b) {
return a.toPair() < b.toPair();
}
We know it can be optimized a little if for even blocks we use the reverse order for the right boundary:
struct Query {
int l, r, idx;
inline pair<int, int> toPair() const {
return make_pair(l / block, ((l / block) & 1) ? -r : +r);
}
};
inline bool operator<(const Query &a, const Query &b) {
return a.toPair() < b.toPair();
}
Achieving a better time complexity
We can achieve 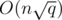 complexity for Mo's algorithm (still assuming that insertions and deletions are O(1)). Note that
complexity for Mo's algorithm (still assuming that insertions and deletions are O(1)). Note that 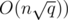 is always better than
is always better than 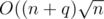 . We can prove it as follows:
. We can prove it as follows:
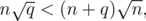
n2q < n(n + q)2,
nq < n2 + 2nq + q2,
n2 + nq + q2 > 0
But how this complexity can be achieved?
Relation to TSP
At first, notice that changing the segment (l1;r1) to (l2;r2) will take |l1 - l2| + |r1 - r2| insertions and deletions.
Denote the queries as (l1;r1), (l2;r2), ..., (lq;rq). We need to permute them to minimize the number of operations, i. e. to find a permutation p1, p2, ... pq such that total number of operations
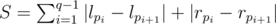
is minimal possible.
Now we can see the relationship between Mo's algorithm and TSP on Manhattan metrics. Boundaries of queries can be represented as points on 2D plane. And we need to find an optimal route to visit all these points (process all the queries).
But TSP is NP-complete, so it cannot help us to find the optimal query sorting order. Instead, we should use a fast heuristic approach. A good approach would be the use of recursive curves. Wikipedia says about using Sierpiński curve as a basis to find a good TSP solution.
But Sierpiński curve is not very convenient in implementation for integer point coordinates, so we will use another recursive curve: Hilbert curve.
Hilbert curve
Let's build a Hilbert curve on a 2k × 2k matrix and visit all the cells on the matrix according to this curve. Denote ord(i, j, k) as the number of cells visited before the cell (i, j) in order of Hilbert curve on the 2k × 2k matrix. The following picture shows ord(i, j) for each cell on the 8 × 8 matrix:

Now we can write a function to determine ord(i, j, k). It will do the following:
- Divide the matrix onto four parts (as Hilbert curve is built recursively, each part is a rotated Hilbert curve).
- Determine, in which of the four parts the cell (i, j) is located.
- Add all the cells in the previous parts. There are 4n - 1·k or them, where k is the number of parts visited before the current one.
- Recursively go into the selected part (do not forget that it can be rotated).
The code looks in the following way:
inline int64_t hilbertOrder(int x, int y, int pow, int rotate) {
if (pow == 0) {
return 0;
}
int hpow = 1 << (pow-1);
int seg = (x < hpow) ? (
(y < hpow) ? 0 : 3
) : (
(y < hpow) ? 1 : 2
);
seg = (seg + rotate) & 3;
const int rotateDelta[4] = {3, 0, 0, 1};
int nx = x & (x ^ hpow), ny = y & (y ^ hpow);
int nrot = (rotate + rotateDelta[seg]) & 3;
int64_t subSquareSize = int64_t(1) << (2*pow - 2);
int64_t ans = seg * subSquareSize;
int64_t add = hilbertOrder(nx, ny, pow-1, nrot);
ans += (seg == 1 || seg == 2) ? add : (subSquareSize - add - 1);
return ans;
}
Assume the matrix has size 2k × 2k, where 2k ≥ n (you can take k = 20 for most cases or find minimal such k that 2k ≥ n). Now denote oi as ord(li, ri, k) on this matrix. Then sort the queries according to their oi.
Here is the proof why this works in 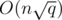 time. Suppose we have n = 2k and q = 4l, where k and l are some integers. (If n and q are not powers of 2 and 4 respectively, we increase them, it don't have any effect on asymptotic). Now divide the matrix onto squares with size 2l × 2l. To travel between a pair of adjacent squares, we need
time. Suppose we have n = 2k and q = 4l, where k and l are some integers. (If n and q are not powers of 2 and 4 respectively, we increase them, it don't have any effect on asymptotic). Now divide the matrix onto squares with size 2l × 2l. To travel between a pair of adjacent squares, we need 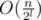 time, so we can travel between all the squares in
time, so we can travel between all the squares in 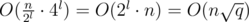 time. Now consider the groups of queries inside a 2l × 2l square. Here we can travel from one query to another in
time. Now consider the groups of queries inside a 2l × 2l square. Here we can travel from one query to another in 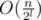 , so we process all such groups of queries in
, so we process all such groups of queries in 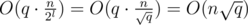 . So the total time to process all the queries is
. So the total time to process all the queries is 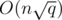 , which was to be proved.
, which was to be proved.
Benchmarks
Let's compare the canonical version of Mo's algorithm and the version with Hilbert order. To do this, we will use the problem 617E - XOR and Favorite Number with different constraints for n and q. The implementations are here:
To reduce the amount of input and output, the generators are built into the code and the output is hashed.
For benchmarks I used Polygon. The results are here:
| n | q |  | Standard Mo time | Mo+Hilbert time | Time ratio |
|---|---|---|---|---|---|
| 400000 | 400000 | 1 | 2730 ms | 2698 ms | 1.012 |
| 1000000 | 1000000 | 1 | 13602 ms | 10841 ms | 1.255 |
| 500000 | 250000 | 2 | 3369 ms | 2730 ms | 1.234 |
| 1000000 | 500000 | 2 | 10077 ms | 7644 ms | 1.318 |
| 600000 | 200000 | 3 | 4134 ms | 2901 ms | 1.425 |
| 1000000 | 333333 | 3 | 8767 ms | 6240 ms | 1.405 |
| 600000 | 150000 | 4 | 4851 ms | 2496 ms | 1.944 |
| 1000000 | 250000 | 4 | 8672 ms | 5553 ms | 1.561 |
| 700000 | 140000 | 5 | 6255 ms | 2854 ms | 2.192 |
| 1000000 | 200000 | 5 | 8423 ms | 5100 ms | 1.652 |
| 750000 | 100000 | 7.5 | 5116 ms | 2667 ms | 1.918 |
| 1000000 | 333333 | 7.5 | 7924 ms | 4009 ms | 1.976 |
| 1000000 | 100000 | 10 | 7425 ms | 3977 ms | 1.866 |
| 1000000 | 40000 | 25 | 9671 ms | 2355 ms | 4.107 |
| 1000000 | 20000 | 50 | 9016 ms | 1590 ms | 5.670 |
| 1000000 | 10000 | 100 | 6879 ms | 1185 ms | 5.805 |
| 1000000 | 5000 | 200 | 5802 ms | 857 ms | 6.770 |
| 1000000 | 2500 | 400 | 4897 ms | 639 ms | 7.664 |
What is interesting, when I ran these codes locally even on the test with n = q (e. g. n = q = 400000), Hilbert version worked about three times faster.
Applicability
As you can see, such sorting order doesn't make Mo's algorithm work slower, and when q is significantly less than n, it works much faster than the classical version. So it is ideal for problems with n = 106 and q = 104. For smaller q solutions with naive query processing can pass.
Thanks to everyone who read this article! I hope it will be useful for someone.
If something is unclear in the post or the post contains bugs, feel free to write in comments.






