Hello, codeforces!
It's time to continue the series of Polish tasks. I've decided to write about my own task one more time. Its name is "cook" (you can submit here). The task isn't very hard, but it uses cute (in my opinion) trick. The statement goes as follows:
There is a cook in a restaurant. He has n (1 ≤ n ≤ 106) orders which he must fill. Every order is a piece of paper, and all orders are speared on a spindle (sharp stick with pierced pieces of paper) in a fixed order which cannot be changed. Normal cook would just take orders one by one from the top of the spindle and fill them in this order, but the cook in this task has supernatural cooking powers and can combine orders to fill them faster. In particular, if at some moment there are k out of n orders still on the spindle, he can choose one of three options:
— He can take the topmost piece of paper and fill this order in time one(k).
— If k > 1, he can take two topmost pieces of paper and fill both orders in total time two(k).
— If k > 1, he can take 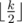 topmost pieces of paper and fill these orders in total time half(k).
topmost pieces of paper and fill these orders in total time half(k).
This task is interactive, so you should communicate with the library and ask it for values of one, two and half. You can ask as many times as you want and assume that the library works in negligible time, so your only limit is the time limit. Please, note, that when k = 2 functions one and half both fills only one order, but they might take different amounts of time. This same applies to other similar situations.
Also, the cook has an energy level, initially equal to e (0 ≤ e ≤ 106). He likes preparing food without any tricks, so whenever he uses the first option his energy increases by one. However, his half combo tires him very much, thus each time when he chooses the third option his energy decreases by one. Cook's energy cannot drop below zero at any time. Of course, we are asked about the minimum amount of time in which cook can finish all orders. Final energy level doesn't matter.
Last thing: memory limit is unusual because it's equal to 8MB.
It's easy to observe that in each moment our situation can be described by the number of orders on the spindle and the energy level, so everything in the task suggests dynamic programming. So, let's denote by DP[i][j] minimum amount of time in which the cook can finish his work if there are last i orders on the spindle and his energy level currently equals j. DP should be initialized in DP[0][i] for all i (cause we don't know how big will be our final level of energy) and the final result will be in DP[n][e]. Transitions are easy. We just have to consider each of the three options. This solution has O(n·(n + e)) complexity, so it's too slow.
To speed it up we need an easy observation. Whenever we lose one point of energy, the number of orders on the spindle becomes about two times smaller. So, we won't use this option more than 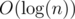 times, so we don't need more than, let's say, 20 energy points. This gives us solution which works in
times, so we don't need more than, let's say, 20 energy points. This gives us solution which works in 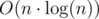 time complexity, whenever cook's energy is greater than 20 (including the very beginning) we decrease it to 20. Unfortunately, we also need
time complexity, whenever cook's energy is greater than 20 (including the very beginning) we decrease it to 20. Unfortunately, we also need 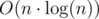 memory. Without cook's third move, we'd be able to keep only last two columns of DP, but to use the third move we need to know values from a column somewhere in the middle. By column k of DP I mean values of DP[k][i] for all i.
memory. Without cook's third move, we'd be able to keep only last two columns of DP, but to use the third move we need to know values from a column somewhere in the middle. By column k of DP I mean values of DP[k][i] for all i.
So, how to optimize the memory? Let's keep two columns of DP (initially columns - 1 and 0). Also, let's say that this pair "points at 0". We'll try to move this pair and make it point at greater values, finally getting our answer when it'll point at n. But I've already mentioned the fact, that to make pair pointing at some k we need to know values of DP from column 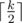 . So, maybe we can keep another pair of columns, which will try to point at value two times smaller than our main pair and will move two times slower? We could, but we'd also need to move it, so we'd need another pair of columns which will point at value again two times smaller (than the second pair), and so on...
. So, maybe we can keep another pair of columns, which will try to point at value two times smaller than our main pair and will move two times slower? We could, but we'd also need to move it, so we'd need another pair of columns which will point at value again two times smaller (than the second pair), and so on...
So, let's just do it! We need only 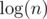 pairs of columns, because when the main pair points at n, every next pair points at value two times smaller, so after
pairs of columns, because when the main pair points at n, every next pair points at value two times smaller, so after 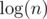 steps we'll decrease this value to zero (or some other small value, depending on implementation). Each pair of columns must know which pair is right behind it. Also, we should define function move(pair_of_columns), which will move chosen pair and (if necessary) will run it recursively on pair which is right behind the pair we are currently moving. It's enough to just run this move function n times on the main pair.
steps we'll decrease this value to zero (or some other small value, depending on implementation). Each pair of columns must know which pair is right behind it. Also, we should define function move(pair_of_columns), which will move chosen pair and (if necessary) will run it recursively on pair which is right behind the pair we are currently moving. It's enough to just run this move function n times on the main pair.
So, we have 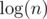 such pairs, each of them can move by one in
such pairs, each of them can move by one in 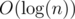 time (because this is the size of a column). Has the complexity just increased to
time (because this is the size of a column). Has the complexity just increased to 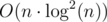 ? No! The main pair will move n times, it's true, but second will move only
? No! The main pair will move n times, it's true, but second will move only  times, third only
times, third only  times and so on. It obviously sums up to O(n) moves, so total complexity stays equal to
times and so on. It obviously sums up to O(n) moves, so total complexity stays equal to 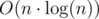 . Memory complexity is now equal to
. Memory complexity is now equal to 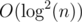 , because we have
, because we have 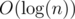 pairs of columns, each of them having
pairs of columns, each of them having 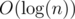 size.
size.
Did you enjoy this blog? I wanted to choose an easier task with a shorter tutorial than the last one. Isn't it too easy? Did you like the trick with decreasing the memory? Let me know in the comments. See you next time! :D






