I recently read this article which summarizes cool cp tricks.
Trick 12 is something uses Euler Tour to solve algorithmic problems on trees. The thing is, I don't know what the difference is between euler tour 1 and 2? If in one euler tour for each node we store when it enters and exits, that gives us continuous segments = subtrees. But what about a path? Apparently another euler tour solves this, but I don't know how it should be represents/how to do it. Could someone please elaborate, preferrably with a diagram?
UPD: Many thanks to saharshluthra for leading me to idea.
I will now try to explain idea in my own words (with hope that it will help others in the future). The idea I was already familiar was this: we create events when we enter a node but not when we exit. We can then query subtrees and update a node in O(logn) with some tree to maintain prefix sums.
The way to query paths is not much different, instead of creating an event for when you enter, you must also create an event for when you exit the node (2 copies). This is because you want to ignore nodes not in the path: nodes with event that end before current one begins in the euler tour. Why are these not in path? Because an exit/ending event indicates backtracking, and if it backtracked from some node A before going into the current node B, node A can't possibly be on path from root to B.
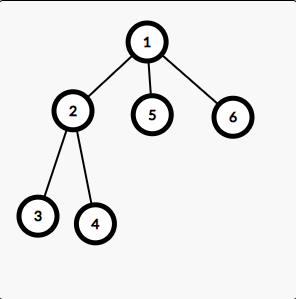
If we visit the nodes in the order [1,2,3,4,5,6] the euler tour we build is [1,2,3,3,4,4,2,5,5,6,6,1]. Notice each number appears twice, one to represent entering and one for exiting (backtracking). Updating a node can be done by adding v in the start position and subtracting v from the end position of a node. Updating subtrees can be done with some range update ideas/keeping track of frequency of starts/ends in some interval. Querying can be done by finding the sum of numbers up to the first position the number shows up.






