The question is about this problem: (Zero XOR Subset)-less.
The problem's editorial describes the solution as follows:
First let 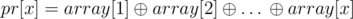 . If we divided the array into k segments, where the right boundaries of these segments are (in increasing order) i1, i2, …, ik (ik must be n), Every segments subset-xor can be represented as pr[ij] subset-xor. Therefore besides maximizing k, we want to guarantee that the any pr[ij] non-empty subset has a non-zero XOR-sum. So we calculate the basis size of pr[1], pr[2], …, pr[n] numbers (binary vectors) under GF(2). Because the basis size will represent the maximum k such that all pr[ij] are linearly independent under GF(2) (no pr[ij] non-empty subset has a zero XOR-sum).
. If we divided the array into k segments, where the right boundaries of these segments are (in increasing order) i1, i2, …, ik (ik must be n), Every segments subset-xor can be represented as pr[ij] subset-xor. Therefore besides maximizing k, we want to guarantee that the any pr[ij] non-empty subset has a non-zero XOR-sum. So we calculate the basis size of pr[1], pr[2], …, pr[n] numbers (binary vectors) under GF(2). Because the basis size will represent the maximum k such that all pr[ij] are linearly independent under GF(2) (no pr[ij] non-empty subset has a zero XOR-sum).
My question is: from the calculated basis size k, we know that we can choose k linearly independent (under GF(2)) pr[ij] values, but how do we guarantee that we can choose these values such that ik = n (as the last right boundary of our chosen segments has to be n)?
Thanks in advance.






