Hi everyone !
We have a static array of size N and Q queries. Each Query given us two integers i and j.
For each query we need to answer what is the maximum frequency of the values of this range.
For example:
A = {3, 4, 3, 4, 4, 1 }
Query(0, 2) = 2 (The value 3 repeat 2 times)
Query(0, 5) = 3 (The value 4 repeat 3 times)
The problem can be found here : http://www.spoj.com/problems/FREQ2/
1 <= N, Q <= 100000, 0 <= A[i] <= 100000
OBS: I would like to know if this problem is possible to solve "online" and the total complexity O(N*log(N)) __ If you have any idea comment bellow, please :D.
Solution using Mo's algorithm (Offline Queries and O(N*sqrt(N)) :
You need to save the value's frequency in a array.
Freq[i] will determine how many times the value "i" has been appears in our current array
Every times you will need to remove a element, decrease Freq[A[i]] by one and check if your answer should be changed
And for Add a element, increase Freq[A[i]] by one and do: answer = max(answer, freq[A[i]])
Code : http://codepad.org/0D7V5uha
Thank you :) and sorry for my bad english











Is there an online way faster than N log^2 N? I couldn't find one.
farmersrice Could you share it? :D
My bad, I was thinking of finding majority, not mode.
It's strongly believed that it is impossible to do so it in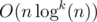 even offline. There is a reduction from multiplication of two binary matrices of size
even offline. There is a reduction from multiplication of two binary matrices of size  to this problem, and the best known matrix multiplication algorithm at the moment is O(n2.37...). This yields a
to this problem, and the best known matrix multiplication algorithm at the moment is O(n2.37...). This yields a 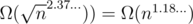 lower bound for this problem, and if you solve it in quasi-linear time it would be a breakthrough whose significance is comparable with solving P vs NP.
lower bound for this problem, and if you solve it in quasi-linear time it would be a breakthrough whose significance is comparable with solving P vs NP.
By the way, the name for the problem is "finding mode on a subsegment".
P.S. Downvoted for "sorry for bad English" part. C'mon, folks, stop adding it to each and every blogpost!
It can be solved online in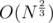 per query :)
per query :)
GreenGrape Could you explain this solution ? :D
Let's split the array into blocks of size A. For each possible range of (some block start, some block end) compute three arrays: frequency of each number, the amount of numbers that give such frequency and one more (I will talk about it later). This will take time and memory.
time and memory.
Now to obtain all existing frequences for an [L..R] segment you have to find the largest range that you've already computed the answer for and stretch it to the left and to the right. This will take O(A) for both ends.
But this is not enough because to answer the "most frequent" query you have to iterate over the entire frequences array which takes O(N) time. Try to guess what should be done to reduce the complexity to with some additional array which I mentioned in the beginning :)
with some additional array which I mentioned in the beginning :)
Talking about A, the optimal choise would be .
.
It can be solved online in time per query and linear memory, though it is rather complicated.
time per query and linear memory, though it is rather complicated.
Same Problem