Microsoft’s Quantum team is excited to announce the Q# Coding Contest – Winter 2019! In this contest you can put your quantum programming skills to the test, solving quantum computing tasks in Q#. Winners will receive a Microsoft Quantum T-shirt!
Quantum computing is a radically different computing paradigm compared to classical computing. Indeed, it is so different that some tasks that are believed to be classically intractable (such as factoring integers or simulating physical systems) can be performed efficiently on a quantum computer. In 2017 Microsoft introduced the Quantum Development Kit which includes the Q# programming language. Q# can be used with Visual Studio, Visual Studio Code or the command line, on Windows, macOS, and Linux.
In summer of 2018 we hosted the first quantum programming contest, which included problems on introductory topics in quantum computing: superposition, measurement, quantum oracles and simple algorithms. This contest will offer harder problems on some of these topics as well as introduce some new topics.
The contest will run from March 1 to March 4. The rules of the contest are:
- The contest will have 12 tasks of various complexity levels.
- To solve each task, you will write Q# code to implement the described transformation on the given set of qubits or to perform a more challenging task. Solutions are accepted in Q# only.
- The solution is correct if it passes all tests from a predefined test set. You will know whether the solution is correct soon after submitting it.
- Participants are ranked according to the number of correctly solved tasks.
- Ties are resolved based on lowest penalty time for all tasks, which is computed as the latest submission time (the time since the start of the contest) for any of the correctly solved tasks. There is no penalty for failed submissions.
- The top 50 ranked participants will receive a Microsoft Quantum T-shirt.
- NO PURCHASE NECESSARY. Must be 16 years of age or older. Game ends 3/4/19. For details, see Official Rules.
We will offer a warmup round the weekend before the contest, from February 22 to February 25. Participation in the warmup round is entirely optional. The warmup round includes simpler tasks on the topics covered in the main contest and gives you an opportunity to get familiar with the contest environment and submission system beforehand, as well as refresh or learn the basics of quantum computing and the Q# programming language. During the warmup round everybody is encouraged to discuss the tasks and the solutions. Once the warmup round is over, we will publish the editorials explaining both the quantum computing logic behind the solution and the Q# implementation on the contest page.
Another great way to prepare for the contest is to solve some of the Quantum Katas. They offer problems on a variety of quantum programming topics, and they are very similar to the ones used in the contest. In fact, the participants of the summer Q# contest will recognize the contest problems in some of the kata tasks :-)
Good luck! We hope you enjoy the contest!
For first time Codeforces users:
- Create user account here.
- Register for the warmup round here.
- Register for the contest here.
- Once the warmup round starts on February 22, access the problems here.
- Once the contest starts on March 1, access the problems here.
Quantum computing and Q# materials:
- Quantum Computing: Lecture Notes by Ronald de Wolf.
- A collection of awesome quantum computing learning resources, including MOOCs and books.
- Q# installation instructions and documentation.
- Quantum Katas — Q# programming exercises.
- Q# Language Quick Reference.
Note that this contest will use Q# 0.4, while the previous contest used Q# 0.2. A lot of code written in 0.2 will still work in 0.4; for details on breaking changes and new features please see release notes.
Update. The warmup round is over; here are the explanations for the problems. See you in the main contest this weekend!













this is so cool. i love that you bring this new innovative stuff on codeforces. i have read a lot on quantum computing and it is definitely the future. moving bits around and all that stuff is awesome. now my only hope is that you won’t mix math and quantum sharp in this contest / this series of contests because Q sharp is very interesting and i really wouldn’t like it to be dirtied up with useless math. i don’t think i’m the only one.
Do you expect higher difficulty than on the first quantum contest, i.e. the T-shirts not being decided on time only?
We are definitely aiming to have more difficult problems in this contest! I asked one of our researchers to write several problems, and I still have to figure out how to solve them myself :-)
We're also going to change scoring to be based on the last solved problem submission time, not on the sum of submission times, so the impact of the time the competitor joins the contest should be reduced.
That being said, Codeforces community has surprised us once already, and I'm not willing to bet that you won't do it again :-)
yeah but math is useless and makes everything unnecessarily harder. so don’t bullshit us with it
Can we expect the t-shirts to be different from the Summer round ones? ;)
Yes, definitely :-)
Good!
Well, time to finish the syntax highlighting I started half a year ago.It's going to take a long time because I'm a lazy shit.I tried solving some of the questions of the previous contest today, but I was getting a lot of "denial of judgment" and "compilation error" errors, even when trying to use the official solution provided. Does anyone know what is the problem?
Specifically for problems B3 and C1.
The checkers of the previous contest have not been updated to the new version of Q# yet. I'm investigating this, but this might take a while. For B3 and B4, for example, the only change I had to do in the reference solution was switch from ";" to "," as a separator between array elements — in Polygon it just worked, but I'm not sure why this gives me "denial of judgement" on the website...
If you want to practice on those problems, you can solve them in the Quantum Katas — they are migrated to 0.4, and as a bonus you get error messages on your machine, not via Codeforces interface.
I checked the Quantum Katas, and they are amazing, but I think I found a mistake, and I don't know how else to report it.
In the 4th Joint Measurement task, it says the output should be "0 if qubits were in W state, 1 if they were in the second superposition."
But the solution given has the reverse, returning 1 for W and 0 for the other.
Nice catch, thank you! I've opened a PR to fix this.
(If you have a GitHub account, you can report possible issues with the katas directly in Issues)
The checkers have been updated now. The problems that were affected are B3-B4, C1-C2 and E1-E2.
Is there a more extensive / detailed documentation for Q#? At this moment one can only guess what adjoint controlled distribute means at the end of an operation. I've seen it in the katas for Superposition. A little more explanation in the docs or somewhere about functors would be nice. Or is there a place and i didn't manage to find it?
https://docs.microsoft.com/quantum contains all Q# documentation. For this particular question, look up Operation Definitions.
https://codeforces.com/contest/1001/submission/50058667
I wonder if the checker is updated since the error message is from the checker... Also, I tried a submission that has passed the test before and it got a CE verdict on the same problem.
Nice catch, indeed I missed the problem from warmup round which needed the same update. Should be fixed now.
Fixed. Thanks for your reply :-)
Is it allowed to stream solving the warm-up round on Youtube?
Call it Boring Programming Stream and they won't know XD
Sure :-)
no, it is strictly prohibited in the rules. read the website's rules before using it.
Scheduled for Sunday, 12:00 CET (Polish time), https://www.youtube.com/watch?v=9CsSqvssZto :)
Is this contest rated?
I have the same question
No.
So, the penalty is based on latest time rather than sum of times?
That's good to hear! Last time, if you were one hour late starting the contest, you would get 10 hours added to your penalty...
Yes. This was one of the big issues mentioned in the discussion of the first contest, so we switched to calculating time penalty this way.
Looks like wrong tries are not counted in the total penalty. Also the number of wrong tries is not correctly calculated. It's -1 (one 'free' wrong try) for some reason. EDIT: Oh, I was wrong. It looks like you have free wrong tries if you fail test#1, but higher test fails are counted.
Yes, we've removed the penalty for failed submissions as well — I don't think any of the problems are easy to bruteforce, and racking up penalty for learning the language is just frustrating. We'll see if we need to put it back it for the main contest.
I think forgiving failure on test 1 is a feature in all Codeforces contests, it's not special to this one.
Am I the only one facing trouble to ResetAll qubits? " The called operation does not support the necessary functor(s) for the requested auto-generation of a specialization."
If you specified the operation to have an automatically generated adjoint (as the oracle tasks do with
adjoint autooradjoint invertclause), it can not use measurements (andResetAlljust measures the qubits and flips them if 1 was measured). Automatically generated adjoint reverses the order of operations and performs their adjoints, and you can not reverse measurement.You can either specify adjoint of an operation that uses measurements manually (if it is still a unitary transformation and has an adjoint — for example, implementing rotation using repeat-until-success loop as described here), or you need to "uncompute" the qubits you're going to release instead of measuring them (see this example).
Good to know this before the contest! I kept getting compilation error for ResetAll, as well, and I got really frustrated.
This is exactly why we're running a warmup round before the main event :-)
This is how warmup round went :)
https://cv1.pikabu.ru/video/2019/02/07/1549525232275164028_640x640.webm
For one of the problems, I used ApplyToEach(X,qs) to flip a bunch of qubits. The compiler didn't like it, because for some reason it doesn't play nice with "adjoint auto". What's the reason for that?
After I changed it to a "for" loop, the compiler error disappeared.
adjoint autorequires that each operation in the body has an adjoint.ApplyToEachdoes not have an adjoint even if the operation it applies to the qubits does have an adjoint. You can useApplyToEachAif you need an adjointable version of that, it will work.This is an unfortunate quirk of the language which is going away in one of the future releases. For now a lot of the library functions have to exist in four versions — one with no functors (*), one with adjoint version (*A), one with controlled version (*C) and one with all (*CA).
Is there any limit on the number of extra qubits that are used in the code? I am getting Memory Limit exceeded on Test 8 in both G1, G2. Can anyone help?
Yes, the memory limit on the problem implicitly defines the limit on the total number of qubits that can be used. However, for tasks G1 and G2 you don't need to allocate any extra qubits! I'll publish the editorial for G1 shortly, meanwhile a hint: take a look at task 1.3 from the Grover search kata.
Thank you. I didn't know that there was a library function analogous to n-bit Toffoli. So, I was implementing n-bit Toffoli gate and it required extra qubits.
On a real quantum computer the gate controlled on multiple qubits would have to be decomposed into 1- and 2-qubit gates, so it would indeed require extra qubits — but you'll still be able to use a library and let it take care of the decomposition. These problems run on a simulator, and it can do controlled gates directly, without extra qubits.
I actually implement a 8-bit Toffoli, with only CNOT gate and CCNOT gate, and using 4 extra qubits. It passed the test.
The official solution is definitely much easier, though.
I keep on getting "Invalid initializer expression. Possible initializers are "Qubit()", "Qubit[expr]", or tuples thereof" when I try to use some extra qubits with 'using(qs = Qubit[number])' which is the same declaration as I saw in one of the References. Please correct me. Thanks.
Your code has
using (qs = Qubits[8])(plural), and the type name is Qubit singular, so you have to useusing (qs = Qubit[8]).Take a look at the task 1.1 of the Grover search kata (and remember that the katas come with reference solutions!)
As a reminder, to define a quantum oracle it is sufficient to define its effect on all computational basis states; its effect on superposition states will follow immediately from its linearity.
The operation which implements the AND oracle can be re-worded as follows: given the input register and the output qubit, flip the state of the output qubit if and only if all qubits in the input register are in the state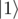 .
.
This is exactly the definition of a controlled version of the X gate: the X gate flips the state of the qubit to which it is applied, and the controlled version of an operation applies this operation if and only if all control qubits are in the state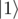 .
.
Q# has built-in gates for the single-controlled X (CNOT) and doubly-controlled X (CCNOT) which most of you have already discovered. In general you can use Controlled functor to create a version of an operation controlled on an arbitrary array of qubits. (It is possible to construct the version of the gate controlled on an array of qubit using only CNOTs and CCNOTs, but this requires allocating extra qubits which can cause hitting memory limit).
With the Controlled functor, the code is a single line:
I solved it like this, but I don't understand a lot of. For example, why I can't check if every qubit is the same (for (i in 1 .. Length(x) — 1) {if (x[0] == x[i]}) and if it is true use CNOT(x[0], y)? Because it isn't working and I think answer will help me with G2, G3 Code: 50399457
What you write something like
if (x[0] == x[i]), you're actually checking reference equality — whether x[0] and x[i] point to the same qubit or to different ones. You can not compare the state of the qubits directly, you need controlled gates for it. So your code from the link effectively flips the answer N-1 times, and then does a CNOT from the first qubit to the answer; for N = 1 this is correct, but for larger values of N it just ignores most of the input.Let's consider applying U1 to the basis state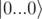 : the result is described by the first column of the matrix you are given. Only the last row of that column contains a non-zero element, i.e.,
: the result is described by the first column of the matrix you are given. Only the last row of that column contains a non-zero element, i.e., 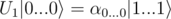 .
.
The operation you need to implement (let's denote it as U1) is a unitary, thus it preserves the inner product of the vectors it is applied to, and in particular it preserves the norm of the vectors it is applied to. The norm of the basis vector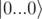 is 1, so the norm of
is 1, so the norm of 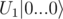 also has to be 1, thus |α0...0| = 1.
also has to be 1, thus |α0...0| = 1.
We can apply the same logic to the rest of the entries in the matrix, and realize that the absolute value of each non-zero element of the matrix has to be 1. For simplicity we can choose all these elements to equal 1:
Now, we need to actually implement the operation which corresponds to this unitary matrix. We can again consider its effect on each basis state, starting with the case N = 2:
This is exactly the result of flipping each qubit independently, which can be done by applying an X gate on each qubit.
You can also think of it as representing the matrix U1 as a tensor product: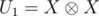 , where
, where 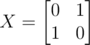 .
.
In the end the code is a one-liner again:
Could you explain how to use the DumpUnitary tool?
1)Clone the quantum katas repo https://github.com/Microsoft/QuantumKatas.git 2)Go to path /QuantumKatas/utilities/DumpUnitary 3)There add your Solve function to the file Operations.qs 4)Change line number 50 to call your function Solve 5)now do $dotnet run in bash 6)After running a file named DumpUnitaryPattern.txt is formed. Verify your solution from it. 7) To change the number of qubits change N in Driver.cs
Hope this helps you
In Operations.qs file make a new operation that takes a Qubit array. Here I called it "YourCode" then modify the existing CallDumpUnitary so it passes your new function to DumpUnitaryToFiles like below.
Then run it. Look in your output folder, there are 2 files, DumpUnitary.txt, and DumpUnitaryPattern.txt, that is your output, that is how your code changed the qubits that got passed into it. If you want to change N, the number of qubits, change the N value in the Driver.cs file's static Main method, run it and now look at your files, they are now a 2^N x 2^N matrix of whatever you changed N to.
Then when you want to submit basically copy all the code inside YourCode and paste it in their solve template where it says "//your code here".
Custom Invocation is not expected to be working, is it?
It looks like lack of Driver and Main leads to compilation error, whatever is sent as Source and Input.
It should be working, same as in the previous contest. Here is the signature of the code you should use to run it (note that the namespace and operation name have to match this code exactly, since this is what is called from C#)
namespace Solution { open Microsoft.Quantum.Primitive; open Microsoft.Quantum.Canon; // ------------- Operation which is called from C# ------------------- operation RunQsharp () : Bool { Message("Hi!"); return true; } }This is what is returned to output if I copy this code to Source:
Hmm, interesting, if you run this in custom invocation of the summer contest (https://codeforces.com/contest/1002/customtest) it will work, but in this contest it fails, even though the language is the same.
We'll look into it, thank you for bringing this up!
It is fixed now.
I try to solve the Chessboard Unitary problem and have the correct matrix output by DumpUnitary. But in the contest, I get WA 1. What could have gone wrong?
Comes out, my matrix was of the desired pattern but not unitary. I guess it would be a good idea to add a unitarity test to the DumpUnitary.
Im not very familiar with quantum mechanics, so i have been trying to solve the Unitary problems by manipulating vectors. I keep coming up against the wall of the 1 vector (a n*n vector with all weights being equal). For one single qubit a set(One, x) plus H(x) gets the desired result, but I am clueless as how to extend this to more than one qubit.
(For context, the 3rd problem is very "easily" solved by a controlled 1 gate followed by negating the upper half, and the second by splitting the qubits into even and odd, and applying the 1 gate to both sets individually)
Edit: its very posible this way of approaching the problems is just incorrect;
Do you mean 1002A1 - Generate superposition of all basis states? You can find the solution to it in the editorial for the summer contest.
Quantum computers are fairy tales and will never be constructed due to Quantum Zeno Effect. Better give us more practical special contests related to web design.
Quantum Zeno Effect isn't a problem for quantum computing, as it requires constant measuring. The usual quantum computation scheme is to prepare the system, then let it evolve on its own, and only at the end there is a measurement. If you solved the problems, you maybe noticed that the problems don't require making measurements, until the moment you check if the answer is correct (except last year's problem that explicitly asked for measurement).
However, it is true that we are still very far from creating fully-scalable universal quantum computer, and with current state of knowledge it seems impossible. The existing "quantum computers" are either very small (~15 qubits) or not fully entangled. The problem is, there are two competing requirements: control and isolation from environment. If the qubits are too weakly coupled with the environment, it is impossible to control them. On the other hand, if they are too strongly coupled with the environment, the information flows to the environment and results in errors in the computation. There are many candidate systems for physical qubit implementation, but all of them suffer in at least one of these issues.
Nevertheless, developing the theoretical base of quantum algorithms can be made even without a working quantum computer and will certainly become useful one day. Some of them don't require full capability of a perfect quantum computer and can be implemented on the easier defect ones. The theoretical quantum informatics also results in quantum error correction protocol, which loosens the criteria for errors.
Forgive me for replying to (I suppose) a trolling attempt, but the information from that post isn't that easy to verify (apart from being rude, which is obvious) so I thought I can clarify a little.
Why is the sequence of operations
Giving me Wrong Answer in G2?. I just wanted to do the Quantum analog of De Morgan, but apparently I am failing :)
You should do
MultiX(x)again, cause you shouldn't change the state of given input.Thank you very much! Although the problem doesn't say so anywhere (the Microsft docs "encourage" you to do so, though). In any case, should'nt it just throw a "Runtime error" or something in cases like this?
Not completely sure, but I remember seeing the author saying that they turn all RE into WA.
The problem does say so: "... performs a transformation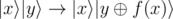 " — this means that x is left unchanged after applying the operation.
" — this means that x is left unchanged after applying the operation.
I tried to draw a better line between Wrong Answer and Runtime Error failures; currently any solution that fails the problem-specific checks (such as returning qubits in a state other than expected or using measurements in a task which prohibits them) should be judged as WA, and any solution that fails more general checks (such as releasing allocated qubits in non-zero state or trying to access array elements outside of array bounds) should be judged as RE. In this case the qubits are returned in the state other than expected, so the judge gives WA.
Oh ok , cool! Didn't thought you would verify the input qubits too.
U4: the same form of the matrix, but the top left 2 × 2 square is anti-unitary and the bottom right (2N - 2) × (2N - 2) is all 'X'-s.
I can't think of a way a unitary can enforce that the OR of the last N-1 qubits remains unchanged! How to solve this?
I've tried something along the lines of:
But its pattern is:
I have no idea how, just throwing it out there. Maybe I should've written U4e+3.
If it was solvable, I'm guessing the solution would be based on the 1e-5 threshold — creating a matrix with not exactly zero coefficient for , but something close enough.
, but something close enough.
Let's apply controlled Hadamard gate on the Suffix using the Or of the Suffix. We can then choose randomly an index from the Suffix and enforce its state to be One. This should follow the pattern you described but I'm unsure if it's a unitary.
Resetuses measurement, so you can't do that.We can enforce One using another temp QuBit, which have the same state as the qubit in the random index (using
CNOTandX), and applyingControlled Xon the random index using both the temp and the Or but I don't think treating QuBits this way is correct.When you use extra qubits and
Controlledoperations, keep in mind:I've thought about this for long enough and it really isn't a warmup problem — if it has a solution, it's not a simple elegant solution.
Xellos — you seem to have a much better grasp on this stuff than I do. I asked Nickolas during the warmup round if there existed a general method for devising an arbitrary matrix. Nickolas answered right after the regular contest ended and said finally can answer this question now contest has ended and yes it is possible, here is link to paper:
https://arxiv.org/pdf/1306.3200.pdf
I'm going through it but don't understand any of it, certainly not enough to implement it. Does it make sense to you?
Could you use this to implement U4?
It's approximation, so you can't use a fixed number of gates to get an exact matrix you want (in general, maybe it works for U4 but there's a specific solution for U4 that doesn't use this anyway). On the other hand, it uses a much more limited set of gates than we have.
Have you tried incorporating the R transformations? Like Rx, Ry, Rz? According to the dump tool the imaginary component counts just as much as the real component. I think in order to pull off your proposed U4 maybe working in Y and Z as well H and X.
I got it so the left top 2x2 matrix were unique values unseen in the rest of the matrix and I feel like I can exploit that to turn that upper left 2x2 into an anti-unitary but not sure how.
But at this point I have no idea what I'm doing, I just toss up X's, H's, Controlled X's, Controlled H's, Y, Z, T, S, etc. Until it finally does what I want. So don't take my word for it.
Yeah, R should be useful. For example, we can convert the last qubit into "pure if and only if everything is
if and only if everything is  " easily. Still, more complex operations (no pun intended) are more complex to use, so the question becomes less "which operations?" and more "how?".
" easily. Still, more complex operations (no pun intended) are more complex to use, so the question becomes less "which operations?" and more "how?".
What do you mean by anti-unitary? In mathematics anti-unitary is anti-linear map, and you can't merge matrix that represent linear map and matrix that represent anti-linear map as blocks of the bigger matrix. This is just ill-defined.
Did you even read U3?
Ah, you wanted to say "anti-diagonal". Should've guess that.
Anti-unitary is a common notion and it's very different from "anti-diagonal".
Yeah, that's what I meant. I pay less attention to precision when it's just a rough idea in the context of the previous problem.
Well, I've gotten close. 2 cells missing. I can't seem to get rid of them and get them above epsilon, though I can push them around in neat ways with CNOT and SWAP, just no matter what I tried yet they stick around. Its pretty clean as well, the zeroes are pure zeroes, and the 2 upper left are pure 1.0. The 2 problem cells are pure zeroes as well, not sure how to mix them in and swirl them around to pick up some value without disturbing the other zeroes.
Well I have N = 2 or 3 working, I feel like the pattern is in the alternation of CNOT and Ry applications, but I have no idea what the pattern is just yet for N>3.
Xellos — Well here is your proposed U4 working for 2 <= N <= 5. Top left is 2 × 2 square is anti-unitary and the bottom right (2^N - 2) × (2^N - 2) is all 'X'-s.
Good job!
Why is this sequence of operations giving wrong answer on U3. I checked with DumpUnitaryTool. I know what littleEndian means. Can someone help me?
Nope. Its wrong for every N, according to DumpUnitary.
DumpUnitary's Output follows littleEndian. So for n=2, should I get
or this?
DumpUnitary follows the same convention as the statement (and the checked in UnitaryPatterns kata), so you should get the first pattern, but your solution produces the second one.
Here is the editorial for the round: https://assets.codeforces.com/rounds/1115/warmup-editorial.pdf
Is there a general algorithm to make the matrix look anyway you want, like a Fast Fourier Transform equivalent or something similar?
The problem is that the pattern itself doesn't specify the elements of the matrix. There is a Quantum Fourier Transform that decomposes a unitary matrix into simpler unitary matrices.
Now that the main contest is over, I can finally answer this question :-)
There are ways to implement a unitary once you have figured out the coefficients it has; one such way is described here. This method, however, is fairly slow — it times out on the largest test in each of the harder D problems.
Do you (or anyone, feel free to answer) know what Z[i,1/sqrt(2)] means in the paper? I thought Z was integers like https://en.wikipedia.org/wiki/Integer
But the hollow Z seems to mean something different in this paper.
So if I understand the paper correctly, but vaguely, you need to devise a U unitary operation that will give you what you want, then this algorithm will construct the arbitrary U operation out of Clifford + T gates for you so when it is applied it changes the identity matrix to the output that you want. Is that the main idea of it? I could be completely wrong, the paper seems above my head at this point.
So like the problem D2, I got a matrix 2^3 x 2^3 for N = 3 like
And I could flip it so the small this part pointed to the upper right, but not top left.
But I couldn't figure out how to flip it like this, its gotta be elementary because it looks like an "anti-diagonal matrix transpose" to flip it from pointing to lower right to pointing to upper left.
Not sure what the proper term is, I figure transpose flips along main diagonal, what I was looking for is a flip along the anti-diagonal. Probably reference implementation just constructs it easily in one shot, but I felt so close when I had it pointing down and right.:
But instead, using the ideas in the paper, I could formulate coefficients for a U that gives me the correct output. Then once I have devised that, the algorithm will tell me how to construct U from Clifford and T gates and possibly up to two ancilla in order to create that arbitrary U operation?
There is a way to decompose any unitary matrix to a product of CNOT gates and a single qubit gates. It's in the famous Nielsen and Chuang book, page 189. I used it in my solution of D6. Though not in a straightforward way.
When will the problems be added to practice session?
They should be available now.
For problem G3, do you really need the ancillary qubits?
You can just CNOT(x[0],x[N-1]), CNOT(x[1],x[N-2]), etc. Then the second half of the array will be all 0s iff the original array was a palindrome. Then revert the CNOTs at the end,
It is possible to solve this problem the way you described as well. The solution I described felt more natural to me, I guess. It has the additional benefit of allowing me to explain in more detail the use of ancillas with uncomputing them in the end instead of measuring, which is a very frequent source of confusion.
This is a really neat solution! I was wondering how I could solve it without using extra memory, since I kept running out of memory for the last test case when using n ancillary qubits.
Yeah, that is how I solved it, I never thought of using extra qubits, at the time I didn't think it was allowed, but I guess it is allowed as long as you don't measure them and you also undo your operations on the ancilla at the end. But this is what I came up with, took me 13 tries since I struggled more with the fact that ranges are inclusive and the arrays are zero based, kind of a rare pairing of paradigms. And no while loop is available I could find, so I couldn't do
Which seems like the most natural control structure for palindromes to me. So my failed submissions were largely from off by one errors dealing with these inclusive ranges. It would be a nice addition to Q# to have regular for loops and while loops, so you can do for(mutable i=0;i<N;i++) or while(i<j), etc. Most people are just so used to zero-based, right exclusive thinking that when we, well at least I, have to think about inclusive ranges its like learning to ride a bike again, I actually have to think about it. But anyway I digress.
Main idea is looping i through 0 .. N/2 and CNOTing the palindromic partners, turns out this operation is easily reversible and so legal in these oracle questions.
So CNOT has a truth table like this:
So left, qs[i] always stays the same, while qs[N-1-i], the right, the target, is assigned a zero if and only if qs[i] and qs[N-1-i] are the same, and its assigned a 1 if they are different, almost like classical XOR except your output is the second operand, almost like take some unknowns A,B in {0,1} and you are doing B = A XOR B;
So lets take a string, "01011011010", loop through i in 0 .. N/2-1, and CNOT qs[i] with its antipodal partner qs[N-1-i], if they are the same then qs[N-1-i] will be 0, so also after that flip it with X(qs[N-1-i]) because later we will re-use our bitwise AND solution from the problem before.
So applying this to my example "01011011010" it will end up as "01011011111", then Controlled X on the last N/2 qubits with y as target to test for a bitwise AND on the N/2..N-1 range, if they are all 1s its was a palindrome, if not a palindrome then there will at least be one zero in the range and y won't be flipped. Then take care of edge case where Length(qs)==1, since length 1 is always a palindrome but there is nothing to CNOT it with so if length is 1 just flip y with X(y) and return. Unless maybe Controlled X on an empty range is always true? Wasn't sure so I handled as a special case.
Then how to undo it? Well look at the truth table, well if left is 0 and right is 1 then after a second CNOT right stays 1, then X flipped again and right is back to 0, its original value. Remember if right is 1 then the original was a match, and left is unchanged, and its a 0, so right must have been a 0 as well. And so going through the truth table you see just applying the same operation again reverts the array back to its original values.
Take left is 0 and right is 0 then they weren't a match originally, because right == 0, so applying second CNOT leaves right == 0, then X flipped and its a 1 again, like we expect, since right is 0 it wasn't a match originally and the unchanged 0 on the left means right must have been a 1 originally.
I'm probably rambling at this point but you can go through the truth table and see its undoable just by reversing the operation along the same right half range.
I think Q# partial application technique is a bit terrifying in the QM context. Unitary operator is not unitary anymore if you look just on some subset of qubits.
They still are unitary operators; they're just tensor products of other unitary operators, with the identity for the qubits you're not looking at.
No. Try to describe what is
SWAP(q,_)where q is some fixed qubit.Nothing. It doesn't exist. There's no such operation defined in the language.
I'm pretty sure that
is a legal code :)
If you are trying to be sarcastic, then don't :)
There are a lot of novices that can't catch that.
That's the same as
SWAP(q1, q2). q1 isn't fixed, it's a mutable qubit. Unless by "fixed" you mean "a variable", i.e. fixed symbol instead of fixed value.Are there any plans to publish editorial to contest itself?
And/or include the contest tasks into Katas along with Reference?
Yes, of course, we've published the editorial here.
We'll definitely publish the tasks as part of the Katas (and a couple of other tasks which were not a great fit for the contest but will be great for the Katas). It will just take some time — the code is mostly the same but the presentation differs, so contest tasks need a little work to be ported to the kata format. The first PR is already up :-)
I'm looking at the final standings and I'm afraid I have no clue how the scoring works. What does '+' or '+2' mean? What does '-3' mean? How is the penalty calculated? Does it depend on the times, and/or these '+' and '-'? If so, how?
A detailed explanation would be much appreciated.
Cheers.
Any submission with a '+' is a solved problem. Number means how many incorrect attempts it took before solving the problem (no number = solved at first try). The time below is when the problem was accepted. Problems marked with a '-' are not solved, and again the number is how many incorrect attempts there were.
In this contest, the first thing that counts is the number of problems solved. Then, the tie-breaker (marked 'penalty') is the time of the last correctly solved problem.
In some other contests, each wrong try on the correctly solved problems gives additional penalty (usually 20 minutes), but here there is no rule. The incorrect tries for unsolved problems don't matter (but they are useful to show during the contest because they will be important if the problem gets solved).
Ah, and I see now the penalty number is literally the number of minutes since the start. Thank you very much for the clarification!
Why are people disliking a genuine question like this?
I can't get the T-shirt, greens never get T-shirt!
Why not? In the previous Q# contest #34 was a green coder, and we most definitely shipped a T-shirt to them :-)
Hi, I'm not able to understand why this code gives compilation error. Please help
namespace Solution { open Microsoft.Quantum.Primitive; open Microsoft.Quantum.Canon;
operation Solve (x : Qubit[], y : Qubit) : Unit { body (...) { mutable f = -1; set f = 0; } adjoint auto; }} Link: https://codeforces.com/contest/1115/submission/50589565
Mutable variables don't allow adjoint variant of the operation to be generated automatically.
I still get compilation error after removing adjoint auto. For some reason it compiles if I remove the set f = 0; line.
If you remove
adjoint auto, the problem G1 will fail compilation because this specific problem requires the operation to have an adjoint specified. If you removeset f = 0, you still have a mutable variable but it's never updated, so it's the same as an immutable variable, and adjoint can get generated automatically.thanks :) I have one more doubt, suppose I want to set a mutable variable to some value and adjoint auto is mentioned how do I do this ?
You can specify adjoint in a different way (for example, manually — the problem requires an adjoint but doesn't restrict how it has to be specified), or you can extract the mutable variable into a function (if it is part of a purely classical processing, for example, in this task).
I just tried it without adjoint auto in custom invocation. No compilation error.
Given the fact 9 months has passed, I still haven't received my T-shirt. sad... Can I track the package in someway?