Qualification Round and its analysis were prepared by Chmel_Tolstiy, aropan, Romka, SobolS, Ra16bit, snarknews and Gassa.
1732 participants have started in the Qualification Round of Yandex.Algorithm, 1606 of them have made at least one attempt, 1558 have solved at least one problem. Interestingly, the number of registered participants was 3397 which is almost twice as much as the number of participants who have started the round. We don't know why is that.
As the qualification round was a virtual contest, participants could choose the most convenient time to compete. The maximum number of participants online (around 280) was at the start, the minimum number — between 3 a.m. and 4 a.m. Moscow time (around 20 participants). First one chronologically who solved all 6 problems was Scott.Ai from China; all problems were submitted "open". Soon i.metelsky (Ivan Metelsky, Belarus) who started around 10 p.m. MSK solved problems A-D "blind", E "open" on the second attempt, F "open" on the first attempt and took the 1st place with a very strong result. However, vepifanov (Vladislav Epifanov, Russia) who started 4 hours later solved A, B, C, F "blind" and D, E "open" on the first attempt, and he took the 1st place thanks to smaller penalty time. On Tuesday morning, first place was taken by world champions from ITMO: first eatmore (Evgeny Kapun, ACM ICPC world champion 2009 and 2012) who started at 11 a.m. solves all 6 problems "blind"... but he was the leader only for several hours: with the same strategy but better penalty time, current world champion tourist (Gennady Korotkevich, Belarus) bypasses him. 24 hours after the start of the Qualification Round the top-3 is Korotkevich — Kapun — Epifanov. In the Test Round, Gennady Korotkevich was second, Vladislav Epifanov was third. The Test Round winner — Антон Лунёв (Anton Lunyov, Ukraine) — started close to the end of the Qualification Round. He solved A, B, F, D "blind", then solved E "open" on the second attempt, then solved C "blind" and took the final 3rd place from vepifanov who moved to the 4th place. Thus all three winners of the Test Round got into top-4, but in a different order. Evgeny Kapun has also advanced to the online rounds from the Test Round, so the best participant who had not advanced before was Ivan Metelsky who finished 5th. Overall 34 participants solved all 6 problems, and the best result of a participant who solved all problems "open" was 9-10 place.
We also noticed that some participants had unexpected problems because of the fact that stdin and stdout were specified as input and output files in the problem statements. Some participants interpreted them as the filenames. Jury decided to rejudge such solutions specifying corresponding filenames; in the future system will use phrases "Standard input" and "Standard output" instead.
Problem A (Ancient Basketball)
In this problem one just had to implement what was described in the problem statement. It is sufficient to create two variables to count points of each team, and after reading records about throws, increase the corresponding variable by the specified number of points. To choose which variable to increase, operator if should be used.
Problem B (Prime Problem)
Let us move 1 to the left-hand side — we get k2 - 1 = p1·p2 or after factorization (k - 1)(k + 1) = p1·p2. As k > 2, both multipliers in the left-hand side are not equal to 1, thus (k - 1) = p1 и (k + 1) = p2 (without loss of generality we can assume p2 > p1). Indeed, left-hand side must be divisible by p1 and p2, so if k - 1 = a·p1 and k + 1 = b·p2, then (k - 1)(k + 1) = ab·p1·p2 = p1·p2, and as a and b are positive integers, a = b = 1. If k - 1 was divisible by p2, it would turn out that k - 1 = p2, k + 1 = p1, but it is a contradiction with p2 > p1.
So, the problem is now reduced to searching for such k that both k - 1 and k + 1 are prime (so-called "twin primes"; interestingly, it is not yet known whether the set of such primes is finite or infinite).
Under the given constraints this search can be implemented in any way, even searching through all (not only even) k and while checking primality searching through all possible divisors up to the number itself. Given that n ≥ 4, "empty" answer is impossible as k = 4 satisfies the equation.
Another way is to factorize k2 - 1 and check that the factorization is just a product of two primes.
Problem C (Board Game)
Answer for the first question is very easy to compute. It is the total number of atoms in all the groups. It is equal to 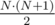 .
.
To answer the second question, let us first reformulate it. It is known from game theory that position in such game is losing if 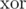 of numbers of atoms in all groups is equal to 0. So, we have to find the number of first moves such that after each of them
of numbers of atoms in all groups is equal to 0. So, we have to find the number of first moves such that after each of them 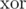 of all group sizes will be 0. Let us denote
of all group sizes will be 0. Let us denote  . There is a fast method to compute x. To do it we can use the fact that for any non-negative integer k
. There is a fast method to compute x. To do it we can use the fact that for any non-negative integer k 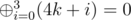 . Thus
. Thus 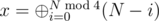 .
.
If we fix group number i to make the first move in it, then the number of atoms that must be left in it after the move is determined unambiguously. It is equal to 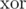 of all other group sizes which is
of all other group sizes which is  . So, if we are able to make the first move from group i it must be true that
. So, if we are able to make the first move from group i it must be true that 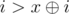 . It is only possible if at position p where x has the highest set bit number i also has set bit. We have to compute the number of such i up to N. Among the numbers less than
. It is only possible if at position p where x has the highest set bit number i also has set bit. We have to compute the number of such i up to N. Among the numbers less than 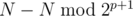 exactly half are such i. If N has set bit at position p,
exactly half are such i. If N has set bit at position p, 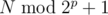 should be added to the answer.
should be added to the answer.
Problem D (Infinite Sum)
Let us make several transformations of the expression:
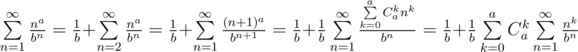
If we denote 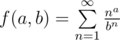 , we get
, we get 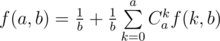
Now we only have to compute the recurrence and output the answer.
Problem E (Homework)
Cases with X = 0 or K = 0 are trivial and can be solved separately. It is advantageous if Gennady solves the maximum number of problems he can each day and the other students can be distributed on the topics, and they can adapt to Gennady's work. If there still exists a topic with at least X problems to solve, Gennady works at maximum this day and solves X problems. If there is no such topic, he takes the topic with maximum number of problems to solve and solves all of them. Thus, it is easy to compute how many problems will be left after Gennady if he works for k days. Then we can use binary search on the number of days and check whether other students will be able to solve all the problems left after Gennady in time.
Time complexity of such solution is 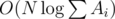 . We should also note that one has to initially sort topics by value of
. We should also note that one has to initially sort topics by value of 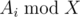 to search for topics with the maximum number of problems to solve when Gennady can't solve X problems. Using the fact that
to search for topics with the maximum number of problems to solve when Gennady can't solve X problems. Using the fact that 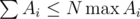 and properties of
and properties of 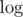 we get complexity
we get complexity 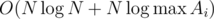 .
.
An alternative solution is to consider the optimal strategy of other students. When we know the optimal strategy for Gennady, we can determine how the other students should work: first they have to solve problem in the topic with the minimum value of 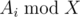 and solve this topic until
and solve this topic until 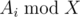 becomes equal to 0. When such topics are all gone and there are still problems to solve, they can choose any topic and solve problems in it until all problems in the topic are solved. So, we have to find out what happens first: Gennady has no more topics with Ai ≥ X, or students have no more topics with
becomes equal to 0. When such topics are all gone and there are still problems to solve, they can choose any topic and solve problems in it until all problems in the topic are solved. So, we have to find out what happens first: Gennady has no more topics with Ai ≥ X, or students have no more topics with 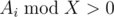 .
.
Time complexity:  .
.
Problem F (Atoms: There and Back Again)
Number of groups doubles after each division. Thus if N is not a power of 2, the given state cannot be reached, and the answer is "NO".
Consider the last division, that is, the division of state right before the current state. Group of size X was created from each group. So, at least half of the groups are of size X. Then we can discard those groups and get the same problem with N / 2 groups. If at any step there is no such size that at least half of the groups have this size, the answer is "NO".
To solve the problem we can cluster the groups by size. Then simulate the process described above using heap (priority queue). We can also greedily separate each cluster of same-size groups into parts of sizes that are powers of 2, so that each power appears exactly once, except for the 0-th power (there must be two parts with 0-th power).
Time complexity is  .
.













Thanks for the editorial.
In problem C, the proof of "position in such game is losing if XOR of numbers of atoms in all groups is equal to 0 " can be found here