| Codeforces Beta Round 88 |
|---|
| Закончено |
Дан неориентированный связный граф G из n вершин и n ребер. G не содержит петель и кратных ребер. Пусть у каждого ребра этого графа есть два состояния: включено и выключено. Изначально все ребра выключены.
Также вам даны m запросов вида (v, u) — изменить состояние всех ребер на кратчайшем пути из вершины v в вершину u в графе G, если таких путей несколько, выбирается лексикографически наименьший. Более формально, рассмотрим все кратчайшие пути из вершины v в вершину u как последовательности вершин v, v1, v2, ..., u. Среди таких последовательностей выбирается лексикографически наименьшая.
Требуется после каждого запроса сказать, сколько компонент связности в графе, вершины которого совпадают с вершинами графа G, а ребра совпадают с включенными ребрами графа G.
В первой строке задано два целых числа — n и m (3 ≤ n ≤ 105, 1 ≤ m ≤ 105). Далее в n строках заданы ребра графа в виде a b (1 ≤ a, b ≤ n). В следующих m строках заданы запросы в виде v u (1 ≤ v, u ≤ n).
Гарантируется, что граф связный, а также не содержит петель и кратных ребер.
Выведите m строк по одному целому числу в каждой — ответы на запросы.
5 2
2 1
4 3
2 4
2 5
4 1
5 4
1 5
3
3
6 2
4 6
4 3
1 2
6 5
1 5
1 4
2 5
2 6
4
3
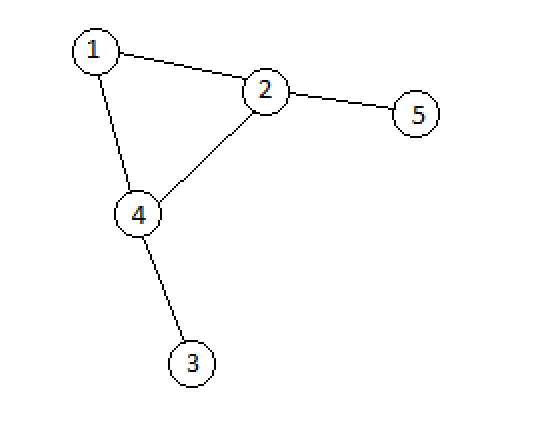
Рассмотрим первый пример. Будем синим выделять на рисунке включенные ребра.
-
Граф до применения операций. В графе нет включенных ребер, поэтому 5 компонент связности есть изначально.
-
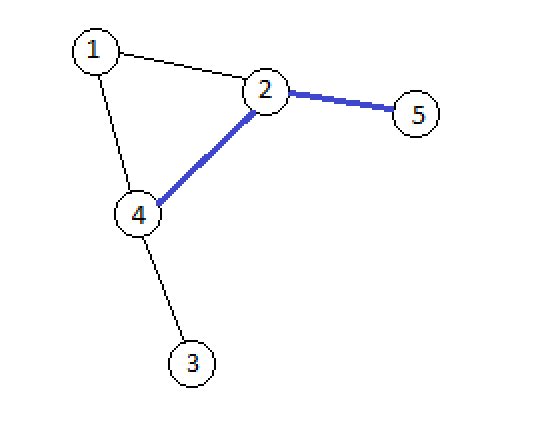
Граф после запроса v = 5, u = 4. Видно, что в графе 3 компоненты, если рассматривать только включенные ребра.
-
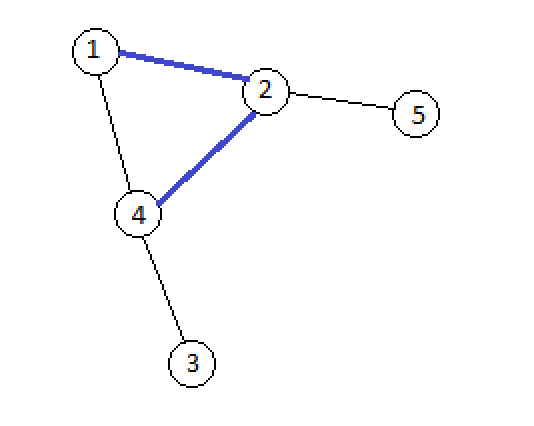
Граф после запроса v = 1, u = 5. Видно, что в графе 3 компоненты, если рассматривать только включенные ребра.
Лексикографическое сравнение двух последовательностей одинаковой длины (k чисел) происходит следующим образом. Последовательность x лексикографически меньше последовательности y если существует такое i (1 ≤ i ≤ k), что xi < yi, а для любого j (1 ≤ j < i) xj = yj.
| Название |
|---|




