You are given a set of n vectors on a plane. For each vector you are allowed to multiply any of its coordinates by -1. Thus, each vector vi = (xi, yi) can be transformed into one of the following four vectors:
- vi1 = (xi, yi),
- vi2 = ( - xi, yi),
- vi3 = (xi, - yi),
- vi4 = ( - xi, - yi).
You should find two vectors from the set and determine which of their coordinates should be multiplied by -1 so that the absolute value of the sum of the resulting vectors was minimally possible. More formally, you should choose two vectors vi, vj (1 ≤ i, j ≤ n, i ≠ j) and two numbers k1, k2 (1 ≤ k1, k2 ≤ 4), so that the value of the expression |vik1 + vjk2| were minimum.
The first line contains a single integer n (2 ≤ n ≤ 105). Then n lines contain vectors as pairs of integers "xi yi" ( - 10000 ≤ xi, yi ≤ 10000), one pair per line.
Print on the first line four space-separated numbers "i k1 j k2" — the answer to the problem. If there are several variants the absolute value of whose sums is minimum, you can print any of them.
5
-7 -3
9 0
-8 6
7 -8
4 -5
3 2 4 2
5
3 2
-4 7
-6 0
-8 4
5 1
3 4 5 4
A sum of two vectors v = (xv, yv) and u = (xu, yu) is vector s = v + u = (xv + xu, yv + yu).
An absolute value of vector v = (x, y) is number 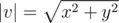 .
.
In the second sample there are several valid answers, such as:
(3 1 4 2), (3 1 4 4), (3 4 4 1), (3 4 4 3), (4 1 3 2), (4 1 3 4), (4 2 3 1).
| Name |
|---|




