Problem A. Elevator
You can either check all four cases or notice, that if we consider front/back equal to 0/1 (b) and decrease a by 1, then a XOR b became the answer (0/1). Time and memory consumption - O(1).
Problem B. Quiz League
Just write one loop: while kth question has already been asked, increase k by one and if k > n let k = 1. Time and memory consumpiton - O(n).
Problem C. Winnie-the-Pooh and honey
One of the possible solutions is direct emulation. Winnie won't do more than 3n iterations (because he can use each jar more than three times). You can emulate each iteration in O(n) (just find maximum in array). Summary time - O(n2) ≈ 104 operations, memory consumption - O(n)
There is another shorter solution: let's notice that order of jars doesn't matter. Let's see how much honey from each jar will be eaten by Winnie and how much will be left to Piglet. If ai ≥ 3k then Winnie will leave ai - 3k kg of honey to Piglet. If ai < 3k then he'll leave only 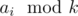 kg. Now solution is one loop. Time and memory consumption is O(n).
kg. Now solution is one loop. Time and memory consumption is O(n).
Problem E. Put Knight!
Petya wins if n is odd, Gena wins if n is even. It's quite easy to prove - just do symmetrical turns.
Problem F. Spiders
Answer is sum of all spiders' lengths. Use depth-first-search (started at all vertexes) to calculate length of each spider.
Problem G. Boom
It's simple realization problem. All you need is two-dimensional arrays and one queue. Code
Problem H. Brevity is Soul of Wit
Notice that there are only 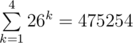 different strings that have length 4 or less. Then notice that each of input strings you can change to
different strings that have length 4 or less. Then notice that each of input strings you can change to 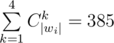 different short words at most (|wi| is length of the ith word).
different short words at most (|wi| is length of the ith word).
Now let's make bipartite graph. One part is all source words, the second part is all short words and there is edge if and only if we can change word from the first part to the short word from the second part. Now our task is just find perfect matching in this graph. It can be done in O(n1· m) ≈ 200· 200· 385 = 15.4·106 operations which is enough.
Problem I. Luck is in Numbers
Unfortunately, my solution for this problem is rather big. If someone know beautiful one share it please.
The main idea is very standard: let's fix some prefix of number, which is strictly greater than such prefix of source number. If we can get known what is maximal happiness for suffix of our number then we can solve the problem by just running down values for each number in suffix and checking that we still can reach necessary value of happiness.
Now solution for this subproblem is just to fill suffix with eights and calculate the answer. It's good but takes a lot of time. We need to store old values and recalculate its in O(1). There are very simple formulas to do it.
Problem J. Minimum sum
Firstly you need to notice that you can turn all vectors in such way that all of them have non-negative coordinates and the answer will remain the same.
And now we have the following problem: find two nearest points from the given set. It's standard divide-and-conquer problem, it's described in Wikipedia.
Also there is simpler solution (added by diogen): let's sort all our points by distance from a random point far-far away. It's oblivious that if some points lie near each other, distance to this far point doesn't vary a lot. And now solution is run down for each point C points near it in the sorted array. C about 200 is enough to got Accepted.











Actually, in Problem
BF,one can compute the diameter of a tree by doing DFS twice. Let u be an arbitrary vertex of the tree, then obtain the farthest vertex v from u and the farthest vertex w from v by two DFS's. The diameter of the tree will be equal to the distance between v and w.Anyway, thanks for the nice editorial.
It's a variation of the divide-and-conquer: you maintain a sorted set (in the y direction), while scanning in the x direction, enabling you to isolate points in rectangles of size mind by mind*2.
In problem J, even my distance was int, i still get ac
I am getting a very very weird error. Can someone please tell me why my solution for the problem F is getting run time error on submitting while it is giving correct output on compiling my local editor or codeforces editor. Here is my Submission
I'm not sure, but maybe it's because you initialize the vector adj inside the main function and it takes too much space.
Apparently this appears to be a codeforces bug.
With minor changes I've achieved this: https://codeforces.com/contest/120/submission/52540219
This is obviously not intended.
I did not get your point. is my code wrong ? or there is some problem with codeforces for checking particularly this problem?