| Codeforces Round 831 (Div. 1 + Div. 2) |
|---|
| Закончено |
У Пака Чанека есть $$$n$$$ пустых карточек в форме сердца. Карточка $$$1$$$ прикреплена непосредственно к стене, остальные же карточки подвешены ровно к одной другой карточке верёвочкой. А именно, карточка $$$i$$$ ($$$i > 1$$$) подвешена к карточке $$$p_i$$$ ($$$p_i < i$$$).
Пак Чанек должен написать на каждой карточке одно целое число. Для этого он выберет произвольную перестановку $$$a$$$ чисел $$$[1, 2, \dots, n]$$$, и на карточке $$$i$$$ запишет число $$$a_i$$$.
После этого Пак Чанек должен выполнить следующую операцию $$$n$$$ раз, поддерживая при этом последовательность $$$s$$$ (изначально пустую):
- Выбрать такую карточку $$$x$$$, что к ней не подвешена ни одна другая карточка.
- Добавить число, записанное на карте $$$x$$$, в конец последовательности $$$s$$$.
- Если $$$x \neq 1$$$ и число на карточке $$$p_x$$$ больше, чем число на карточке $$$x$$$, заменить число на карточке $$$p_x$$$ на число на карточке $$$x$$$.
- Удалить карточку $$$x$$$.
После этого у Пака Чанека будет последовательность $$$s$$$ из $$$n$$$ элементов. Какова максимальная длина наибольшей неубывающей подпоследовательности$$$^\dagger$$$ $$$s$$$ в конце, если Пак Чанек выполняет все шаги оптимально?
$$$^\dagger$$$ Последовательность $$$b$$$ называется подпоследовательностью последовательности $$$c$$$ если $$$b$$$ может быть получена из $$$c$$$ удалением некоторого (возможно нулевого) количества элементов. Например, $$$[3,1]$$$ — подпоследовательность $$$[3,2,1]$$$, $$$[4,3,1]$$$ и $$$[3,1]$$$, но не $$$[1,3,3,7]$$$ и не $$$[3,10,4]$$$.
Первая строка содержит одно целое число $$$n$$$ ($$$2 \le n \le 10^5$$$) — количество карточек.
Вторая строка содержит $$$n - 1$$$ целое число $$$p_2, p_3, \dots, p_n$$$ ($$$1 \le p_i < i$$$) описывающая, к какой карточке подвешена каждая карточка.
Выведите одно целое число — максимальную длину наибольшей неубывающей подпоследовательности $$$s$$$ в конце, если Пак Чанек сделает все шаги оптимально.
6 1 2 1 4 2
4
2 1
2
Ниже представлена структура карточек в первом примере.
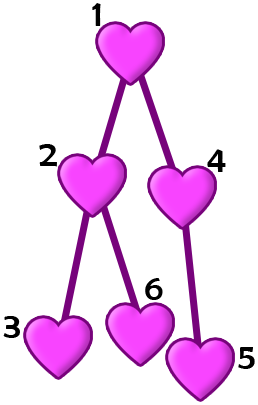
Пак Чанек может выбрать перестановку $$$a = [1, 5, 4, 3, 2, 6]$$$.
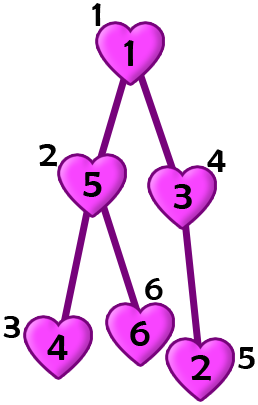
Пусть $$$w_i$$$ — число на карточке $$$i$$$. Изначально $$$w_i = a_i$$$.
Пак Чанек может выполнять следующие операции по порядку:
- Выбрать карточку $$$5$$$. Добавить $$$w_5 = 2$$$ в конец $$$s$$$. Так как $$$w_4 > w_5$$$, значение $$$w_4$$$ становится равным $$$2$$$. Удаляем карточку $$$5$$$. После этой операции $$$s = [2]$$$.
- Выбрать карточку $$$6$$$. Добавить $$$w_6 = 6$$$ в конец $$$s$$$. Так как $$$w_2 \leq w_6$$$, значение $$$w_2$$$ остается неизменным. Удаляем карточку $$$6$$$. После этой операции $$$s = [2, 6]$$$.
- Выбрать карточку $$$4$$$. Добавить $$$w_4 = 2$$$ в конец $$$s$$$. Так как $$$w_1 \leq w_4$$$, значение $$$w_1$$$ остается неизменным. Удаляем карточку $$$4$$$. После этой операции $$$s = [2, 6, 2]$$$.
- Выбрать карточку $$$3$$$. Добавить $$$w_3 = 4$$$ в конец $$$s$$$. Так как $$$w_2 > w_3$$$, значение $$$w_2$$$ становится равным $$$4$$$. Удаляем карточку $$$3$$$. После этой операции $$$s = [2, 6, 2, 4]$$$.
- Выбрать карточку $$$2$$$. Добавить $$$w_2 = 4$$$ в конец $$$s$$$. Так как $$$w_1 \leq w_2$$$, значение $$$w_1$$$ is left unchanged. Удаляем карточку $$$2$$$. После этой операции $$$s = [2, 6, 2, 4, 4]$$$.
- Выбрать карточку $$$1$$$. Добавить $$$w_1 = 1$$$ в конец $$$s$$$. Удаляем карточку $$$1$$$. После этой операции $$$s = [2, 6, 2, 4, 4, 1]$$$.
Одна из наибольших неубывающих подпоследовательностей $$$s = [2, 6, 2, 4, 4, 1]$$$ это $$$[2, 2, 4, 4]$$$. Таким образом, длина наибольшей неубывающей подпоследовательности $$$s$$$ равна $$$4$$$. Можно доказать, что это действительно максимально возможная длина.
| Название |
|---|




