| Codeforces Round 130 (Div. 2) |
|---|
| Finished |
The Berland road network consists of n cities and of m bidirectional roads. The cities are numbered from 1 to n, where the main capital city has number n, and the culture capital — number 1. The road network is set up so that it is possible to reach any city from any other one by the roads. Moving on each road in any direction takes the same time.
All residents of Berland are very lazy people, and so when they want to get from city v to city u, they always choose one of the shortest paths (no matter which one).
The Berland government wants to make this country's road network safer. For that, it is going to put a police station in one city. The police station has a rather strange property: when a citizen of Berland is driving along the road with a police station at one end of it, the citizen drives more carefully, so all such roads are considered safe. The roads, both ends of which differ from the city with the police station, are dangerous.
Now the government wonders where to put the police station so that the average number of safe roads for all the shortest paths from the cultural capital to the main capital would take the maximum value.
The first input line contains two integers n and m (2 ≤ n ≤ 100, 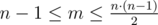 ) — the number of cities and the number of roads in Berland, correspondingly. Next m lines contain pairs of integers vi, ui (1 ≤ vi, ui ≤ n, vi ≠ ui) — the numbers of cities that are connected by the i-th road. The numbers on a line are separated by a space.
) — the number of cities and the number of roads in Berland, correspondingly. Next m lines contain pairs of integers vi, ui (1 ≤ vi, ui ≤ n, vi ≠ ui) — the numbers of cities that are connected by the i-th road. The numbers on a line are separated by a space.
It is guaranteed that each pair of cities is connected with no more than one road and that it is possible to get from any city to any other one along Berland roads.
Print the maximum possible value of the average number of safe roads among all shortest paths from the culture capital to the main one. The answer will be considered valid if its absolute or relative inaccuracy does not exceed 10 - 6.
4 4
1 2
2 4
1 3
3 4
1.000000000000
11 14
1 2
1 3
2 4
3 4
4 5
4 6
5 11
6 11
1 8
8 9
9 7
11 7
1 10
10 4
1.714285714286
In the first sample you can put a police station in one of the capitals, then each path will have exactly one safe road. If we place the station not in the capital, then the average number of safe roads will also make 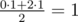 .
.
In the second sample we can obtain the maximum sought value if we put the station in city 4, then 6 paths will have 2 safe roads each, and one path will have 0 safe roads, so the answer will equal 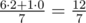 .
.
| Name |
|---|




