First, arrange the problems in order of their difficulties. The authors assume such order: A, D, B, C, E. Now make the tutorial of problems in their order in the contest.
This problem was technical. First, you should erase all occurrences or word WUB in the beginning and in the end of the string. And then parse the remaining string separating tokens by word WUB. Empty tokens should be also erased. Given string was rather small, you can realize the algorithm in any way.
In this problem you could write breadth-first search. The state is the following four elements: number of remaining piles and three strings — three rightmost cards on the top of three rightmost piles. We have two transitions in general case. We can take the rightmost pile and shift it left by 1 or 3 on another pile. If the number of remaining piles become 0 at some moment print YES, else print NO. The number of states is O(N4), the number of transitions 2, so the complexity of solution is O(N4).
In this problem we will find the sought quantity for every vertex and find the maximum value. For this for every vertex v count two values: cnt1[v] and cnt2[v] — number of shortest paths from vertex v to n-th and 1-st vertices respectively. For this you should construct graph of shortest paths and use dynamic programming on the constructed graph (because the new graph will be acyclic). To construct the graph of shortest paths you should leave only useful edges in original graph. It can be done, for example, using breadth-first search launched from vertices 1 and n respectively.
After values cnt1[v] and cnt2[v] are found consider every useful edge (u, v) and add to vertices u and v value (cnt2[u] * cnt1[v]) / (cnt2[n–1]), which is the contribution of this edge in the sought quantity for the vertices u and v. Note that value (cnt2[n–1]) is the number of shortest paths between 1 and n. All said values can be found in time O(N + M). The complexity of solution is O(N + M).
208D - Prizes, Prizes, more Prizes
In this problem every time you get points you should greedily get as much prizes as you can. For this, consider every prize from the most expensive and try to get as much as you can. If we have cnt points and the prize costs p points you can get 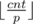 prizes. So we get simple solution with complexity O(5 * N).
prizes. So we get simple solution with complexity O(5 * N).
In this problem you have some set of rooted down- oriented trees. First, launch depth-first search from every root of every tree and renumber the vertices. Denote size of subtree of vertex v as cnt[v]. In this way all descendants of vertex v (including v) wiil have numbers [v;v + cnt[v]–1].
Then we wiil handle requests (v, p) in their order. First, go up from vertex v on p steps to the root using binary rise like in LCA algorithm. Denote this vertex u. If u doesn’t exist print 0 else you should count the number of descendants of vertex u on the same height as vertex v.
For this write all numbers of vertices for every height in some array. Then you should determine which of these vertices are descendants of u. You can do it using binary search in corresponding array. Find the segment of appropriate vertices (because we know the numbers of all descendants of u), find the amount of them, subtract one (vertex v), and this is the answer. The complexity of the solution is O(Nlog(N)).











Can somebody help me for the E problem. How do I calculate the pth ancestor of some vertex. Simply climbing till the root gives TLE. The Editorial says to use the LCA algorithm. How do I use the sparse table to get the pth ancestor?
you can store the 2^i'th ancestor of each node as u do in binary . now for pth ancestor ,visualize p in binary like suppose p i 62 then 62 can be breaked as 32+16+8+4+2 thus u can find it's 32th parent in O(1) as u have already stored then it's 16 th ancestor and so on....it is just like finding x**y in logn time..
My approach is that I am keeping count of pair<node,level> for every node during HLD preprocessing. Then for each query I see its pth ancestor and total number of pair<pth ancestor,pth level> but it giving me wrong ans. Why can you help me?
By Errichto, a great place to learn from !!
An other approach on 208E blood cousins without usage of LCA or binary search: We store the queries offline in a list on the appropriate cousin nodes and then we traverse with a dfs to update level of every node and move queries to the ancestor requested for every cousin. You can use a list to store multiple queries on every node.
A second dfs will parse and update the queries: when every node is recursively pre order processed, it pushes the count of children found on next levels (only on levels required by a query) and zero them. The dfs will continue to the children and uppon return, the final countouts would have been calculated. Previous pushed countouts are restored and updated.
O(N+M) reading O(N+M) first DFS (DFS on N nodes + move M queries to ancestor) O(N+2*M) second DFS (DFS on N nodes + push M counters, process M queries, pop M counters) O(M) print results
Overal complexity O(N+M).
Print results in order of appearance in test file and voila.
Nice
Can you please send a clear code for this concept. It seems interesting.
can you share your code
Hello, For 208E — Blood Cousins problem, could you please explain as to how a binary search helps in counting the number of nodes for the target level. I am referring to the last paragraph of the editorial "count the number of descendants of vertex u on the same height as vertex v"
Thank you in advance.
You can use the concept of discovery time and finish time.If we know the distance of node x , let it be a , then distance of all those nodes will be a + p. For every distance d , we will push all the node's discovery time and finishing time whose distance is d. Now , according to properties of dfs, all the nodes which are in subtree of node x will have discovery time > discovery time of x, and finishing time <= finishing time of node x. Since , we also know that all those nodes are at distance a + p. We will go to that distance vector and find number of nodes which has the above mentioned property. For more clarity, you can check out my Submission :)
Thank you for quick response. Now, I am trying to understand as to how to apply the concept of Discovery/Finish time in trees.
I will keep you posted incase I have any doubts.
Thanks again :)
That part is well explained in CLRS. You might want to take a look at it.
LCA in E?