A very tense moment: n cowboys stand in a circle and each one points his colt at a neighbor. Each cowboy can point the colt to the person who follows or precedes him in clockwise direction. Human life is worthless, just like in any real western.
The picture changes each second! Every second the cowboys analyse the situation and, if a pair of cowboys realize that they aim at each other, they turn around. In a second all such pairs of neighboring cowboys aiming at each other turn around. All actions happen instantaneously and simultaneously in a second.
We'll use character "A" to denote a cowboy who aims at his neighbour in the clockwise direction, and character "B" for a cowboy who aims at his neighbour in the counter clockwise direction. Then a string of letters "A" and "B" will denote the circle of cowboys, the record is made from the first of them in a clockwise direction.
For example, a circle that looks like "ABBBABBBA" after a second transforms into "BABBBABBA" and a circle that looks like "BABBA" transforms into "ABABB".
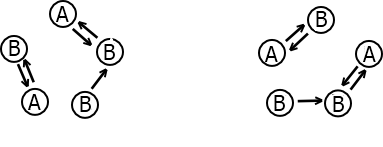 This picture illustrates how the circle "BABBA" transforms into "ABABB"
This picture illustrates how the circle "BABBA" transforms into "ABABB" A second passed and now the cowboys' position is described by string s. Your task is to determine the number of possible states that lead to s in a second. Two states are considered distinct if there is a cowboy who aims at his clockwise neighbor in one state and at his counter clockwise neighbor in the other state.
The input data consists of a single string s. Its length is from 3 to 100 characters, inclusive. Line s consists of letters "A" and "B".
Print the sought number of states.
BABBBABBA
2
ABABB
2
ABABAB
4
In the first sample the possible initial states are "ABBBABBAB" and "ABBBABBBA".
In the second sample the possible initial states are "AABBB" and "BABBA".
| Name |
|---|




