| Codeforces Round 209 (Div. 2) |
|---|
| Finished |
A permutation p is an ordered group of numbers p1, p2, ..., pn, consisting of n distinct positive integers, each is no more than n. We'll define number n as the length of permutation p1, p2, ..., pn.
Simon has a positive integer n and a non-negative integer k, such that 2k ≤ n. Help him find permutation a of length 2n, such that it meets this equation: 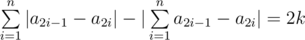 .
.
The first line contains two integers n and k (1 ≤ n ≤ 50000, 0 ≤ 2k ≤ n).
Print 2n integers a1, a2, ..., a2n — the required permutation a. It is guaranteed that the solution exists. If there are multiple solutions, you can print any of them.
1 0
1 2
2 1
3 2 1 4
4 0
2 7 4 6 1 3 5 8
Record |x| represents the absolute value of number x.
In the first sample |1 - 2| - |1 - 2| = 0.
In the second sample |3 - 2| + |1 - 4| - |3 - 2 + 1 - 4| = 1 + 3 - 2 = 2.
In the third sample |2 - 7| + |4 - 6| + |1 - 3| + |5 - 8| - |2 - 7 + 4 - 6 + 1 - 3 + 5 - 8| = 12 - 12 = 0.
| Name |
|---|




