I'm not good in English. So, if you find an mistake in editorial, please, send me a private message.
359A - Table
If there are some good cell, which is located in the first row or in the first column, the answer is two. Similarly, if If there are some good cell, which is located in the last row or in the last column, the answer is two. Otherwise, the answer is four.
Авторское решение: 4968279
359B - Permutation
The answer is a slightly modified permutation 1, 2, ..., 2n. Let's reverse numbers 2i - 1 and 2i for each 1 ≤ i ≤ k. It's not hard to understand, that this permutation is good.
Авторское решение: 4968385
359C - Prime Number
Obviously, the answer is xv. Let sum = a1 + a2 + ... + an. Also let si = sum - ai (the array of degrees). After that let's find value v by the following algorithm: Let's consider a sequence of degrees as decreasing sequence. Now we will perform the following operation until it's possible to perfom it. Take the minimum degree v from the array of degrees and calculate the number of elements cnt, which have the same degree. If cnt multiples of x, then replace all cnt elements by cnt / x elements of the form v + 1. Since the sequence of degrees is a decreasing sequence, we can simply assign them to the end. If cnt is not a multiple of x, then we found the required value v. Also you need to check, that v is not greater then sum. Otherwise, v will be equals to sum.
Авторское решение: 4968346
359D - Pair of Numbers
Quite simple note: if the pair (l, r) satisfies the condition 1 from the statements, then min(l, r) = GCD(l, r), where min(l, r) is smallest number ai from the segment (l, r) and GCD(l, r) is a GCD of all numbers from the segment (l, r). Calculate some data structure that will allow us to respond quickly to requests GCD(l, r) and min(l, r). For example, you can use Sparce Table. Solutuions, that uses segment tree, is too slow. So I think, you should use Sparce Table. So, now our task quite simple. Let's use binary search to find greatest value of r - l:
lf = 0; //left boundary of binary search
rg = n; //right boundary of binary search
while (rg - lf > 1) {
int mid = (lf + rg) / 2;
if (ok(mid)) //ok(mid)
lf = mid;
else
rg = mid;
}
ok(mid) is the function, that determines, is there some segment where min(l, r) = GCD(l, r) and mid = r - l (mid — is fixed value by binary search). If there is some good segment, you should update boundaries of binary search correctly. After that, it's very simple to restore answer.
Some information about Sparce Table
Авторское решение: 4968587
359E - Neatness
You should write recursive function, that will turn on the light in all rooms, where it's possible. Also this function will visit all rooms, which it may visit. Let this function is called paint(x, y), where x, y is the current room. Paint(x, y) will use following idea: Let's look at all neighbors. If there is a light in the current direction (rule 3 from the statement), and the room (nx, ny) (current neighbor) has not yet visited, we will call our recursive function from (nx, ny). Also, we will turn on the light in all rooms, were we were. If some room is not visited by paint(x, y) and lights is on in this room, the answer is "NO". Otherwise, the answer is "YES". After that let's calculate value dist(x, y) by using bfs. dist(x, y) — is a minimal possible distance from the start to the current position (x, y). It's possible to use in our bfs only rooms, where lights is on. After that we will write the same function repaint(x, y). Repaint(x, y) will use following idea: Let's look at all neighbors. If there is a light in the current neighbor (nx, ny) and dist(nx, ny) > dist(x, y) ((x, y) — current room), let's call our recursive function from (nx, ny).After that we will come back to room (x, y). If there is no such neigbor (nx, ny), turn off the light in the room (x, y). Also you should look at my solution for more details.
Авторское решение: 4968657











For problem D, I don't understand why this (4969570) simple solution passed the time limit, it's run in O(n^2) right? And why it passed the worst case (test case #23) just in 46ms! Unbelievable :-O
Correct me if I'm wrong
Notice the operation
r =i+1. It should be O(N2) theoretically, but it's near impossible to make test data that cause it to fail (for example, ai = 2N - i is a case where it performs at least N2 operations).It's not O(N^2), it's O(N*log(Range)) in worst case, in average way faster than original solution. The worst case would be when in every iteration we go far to the left, but just one step right. But for this to happen, consecutive numbers should be divisors of their predecessors, example:
32 16 8 4 2 1
In every iteration we make only one step right(by increasing i), but many steps left. However the input range (1..10^6) limits max steps to the left to log(10^6)=20
Ok, I didn't read you already gave the worst case scenario. But still, N is not the only parameter of algorithm complexity, range is also such. So, if range was infinite, it would be O(N^2), but since it's limited, I would say it is O(N*log(Range)).
Well, actually there are many other ways to solve this problem, my solution uses maps only and the worst time is O(n * (greatest number of divisors for any number))
i.e: 6 has 4 divisors (1, 2, 3, 6)
5605391
Any other explanation for D ?
My solution is a bit different used a stack left , a stack right. You'll push a[i] if stack.top() % a[i] != 0 else stack.pop(); you'll find the farthest element which is divisible by a[i]. 4966411
great solution , I share the same idea with you in the first place but i can't find the way how to caculate L[i] and R[i] . Now I know it could be solve by using stack . Tks a lot :D
meodorewan Can you please explain a little bit. I have been trying to look up some solution that does not use a sparse table. Yours seems the best. I tried to understand your code, but it'd be of great help if you could please explain this solution of yours.
I do not fully understand the solution to D. I have understood till the part where we need to have a data structure which gets GCD(l, r) and min(l, r) in a short time.
Say I use a segment tree for that. Now what? Binary search how? Can someone kindly explain?
for each element i we search for biggest j such that each element in range i...j is divisible by element i , also we search for smallest k such that each element in range k...i is divisible by element i so we have k ... j is maximal good range , we do this for each i
So we basically need only data structure for GCD(l, r) right? No need of min(l, r) then.
Find the largest 'j' such that GCD(i, j) = a[i] and find smallest 'k' such that GCD(k, i) = a[i].
Yes
We want to find the maximum possible length of a segment such that there exists a segment that satisfies both conditions and has this length.
It's obvious that this F(len) = {1 if such segment exists and 0 otherwise } is monotonous so we use binary search.
Now for each of our guesses (for each of mid in bin search) we need to calc F(mid).
We iterate through each segment of length mid and if GCD of all numbers on current segment is equal to minimum of all numbers on the segment then we've just found a satisfying segment (F(mid) = 1). And if we haven't found any then F(mid) = 0.
This is exactly the way described in the blog but a lot more clearer. Now I understand this method. Thank you :)
EDIT : Just tried this method using two segment trees. One for GCD(i, j) and the other for min(i, j). Still getting TLE. What is the reason? Segment tree is slow?
My submission : http://codeforces.com/contest/359/submission/4980867
EDIT 2: Replaced segment tree with sparse table and AC now. Learnt something new :)
I think you have to pre-compute segments by using sparse table which is <O(nlgn),O(1)>. There is a link in tutorial about it.
For D, there is a much easier and faster solution. For each direction(left to right or right to left) see how much you can go with one number. if your number is not divisible any more try to continue it by your current value. The only problem is same number's left and right interval may intersect. Mine: 4974772
I still cannot understand the solution described for problem C. It would be very much appreciated if someone could please explain. Thanks!!
I dont understand author's solution too. I have next solution (it maybe like authors):
at first there is next fraction: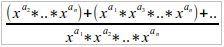
then lets find [max a] — in my example it is a^n
at numerator we can factor out minumum of numerator. it is (without [max a] — at my example [max a] is a^n) or ([sum of a-elements] — [max a]), so then in brackets:
(without [max a] — at my example [max a] is a^n) or ([sum of a-elements] — [max a]), so then in brackets: 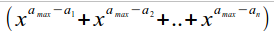
so now the answear is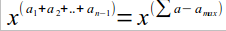
then sum in brackets maybe have addition common divisor for x. For example: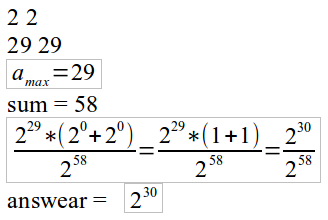
for finding addition common divisor I do next: count different degrees at brackets. and go from degree 0 and try convert count degree of 0 to count degree of 1 and continue. I check that count of degree mod x == 0 and stop if its not so. when stop i can add to answear degree on what i stop. for example: on example stopping on degree 2, so to answear i can add 2. my solution:4986617
on example stopping on degree 2, so to answear i can add 2. my solution:4986617
Thanks mate..
Best codeforces set I have ever participated. The problems were really very interesting with an excellent statement and samples. super like to the authors \m/
in problem E whats the logic behind calculating distance form bfs and using it in repaint
In worst case we will visit only 500*500 cells and 4*500*500 actions needed . Simple dfs is enough . Here's my ac code
The problem D can be solved with a complexity O(n). http://codeforces.com/contest/359/submission/5035770
For problem D, i got ac with tutorial solution. But now i am confused about the complexity. isn't it n*logn*logn*logn? How come it still passed with sparse table but when tried with segment tree, it didn't? Please correct me if i am wrong.
Can anyone explain problem C?
In problem D, why is segment tree slower than sparse table?
Time complexity of segment tree: Build-O(n) and Query-O(logn)
Time complexity of sparse table: Build-O(nlogn) and Query-O(logn)
So, looking at this 2 complexities, isn't segment tree supposed to be faster than sparse table?
query is O(1) in a sparse table.
For problem D, use Left Right for a much easier method :v Link: https://codeforces.com/contest/359/submission/105036790