| Codeforces Round 236 (Div. 2) |
|---|
| Finished |
You have an array of positive integers a[1], a[2], ..., a[n] and a set of bad prime numbers b1, b2, ..., bm. The prime numbers that do not occur in the set b are considered good. The beauty of array a is the sum 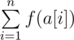 , where function f(s) is determined as follows:
, where function f(s) is determined as follows:
- f(1) = 0;
- Let's assume that p is the minimum prime divisor of s. If p is a good prime, then
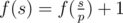 , otherwise
, otherwise 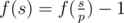 .
.
You are allowed to perform an arbitrary (probably zero) number of operations to improve array a. The operation of improvement is the following sequence of actions:
- Choose some number r (1 ≤ r ≤ n) and calculate the value g = GCD(a[1], a[2], ..., a[r]).
- Apply the assignments:
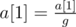 ,
, 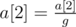 , ...,
, ..., 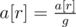 .
.
What is the maximum beauty of the array you can get?
The first line contains two integers n and m (1 ≤ n, m ≤ 5000) showing how many numbers are in the array and how many bad prime numbers there are.
The second line contains n space-separated integers a[1], a[2], ..., a[n] (1 ≤ a[i] ≤ 109) — array a. The third line contains m space-separated integers b1, b2, ..., bm (2 ≤ b1 < b2 < ... < bm ≤ 109) — the set of bad prime numbers.
Print a single integer — the answer to the problem.
5 2
4 20 34 10 10
2 5
-2
4 5
2 4 8 16
3 5 7 11 17
10
Note that the answer to the problem can be negative.
The GCD(x1, x2, ..., xk) is the maximum positive integer that divides each xi.
| Name |
|---|




