402A - Nuts
Let's fix some value of boxes ans. After that we can get exactly cnt = ans + min((k - 1) * ans, B) of sections. So, if cnt * v ≥ a, then ans be an answer. After that you can use brute force to find smallest possible value of ans.
402B - Trees in a Row
Let's fix height of the first tree: let's call it a. Of course, a is an integer from segment [1, 1000]. After that, for the fixed height a of the first tree we can calculate heights of the others trees: a, a + k, a + 2k, and so on. After that you should find minimal number of operations ans to achive such heights. After that we can use brute force to find smallest possible ans for each a from 1 to 1000. For best height of the first tree you should print all operations.
402C - Searching for Graph / 403A - Searching for Graph
I will describe two solutions.
First. Consider all pairs (i, j) (1 ≤ i < j ≤ n). After you should ouput the first 2n + p pairs in lexicographical order.
It's clear to understand, that it is enough to prove, that 0-interesting graph is correct or - 3 -interesting graph is correct. We will prove for - 3 -interesting graph, that it is correct. This graph consists of triangles, which have an common edge 1 — 2. Let's fix some subset of vertexes, which does not contains vertexes 1 and 2. In such sets there are no edges. Let's fix some subset, which contains exactly one vertex (1 or 2). In such subsets there are exactly k - 1 edges, where k is the size of such subset. In other subset there are exactly 2 * (k — 2) + 1 edges, where k is the size of such subset.
Second. Let's use some brute force, to build graphs with 0-interesting graphs with sizes 5, 6, 7, 8, 9 vertexes. Now, to build p-interesting graph with n vertexes, We will build 0-interesting graph, and after that we will add to it p another edges, which is not in the graph. We will build 0-interesting graphs using the following approach: Let's took k disjointed components, from graphs with number of vertexes from 5 to 9, in such way that there are exactly n vertexes in graph.
402D - Upgrading Array / 403B - Upgrading Array
I will describe two solutions.
First. Dynamic programming approach. Let's calculate an DP d[i][j] — which is the best possible answer we can achieve, if current prefix has length i and we used operation of Upgrading last time in position j. It is clear to understand, that we should iterate i from n to 1, and j from n to i. There are only two transitions:
- First, d[i - 1][j] = max(d[i - 1][j], d[i][j]) — we will not use operation of upgrading of array in the current position.
- Second, d[i - 1][i - 1] = max(d[i - 1][i - 1], d[i][j] + f(tgcd[j]) * i - f(tgcd[i - 1]) * i — we are using an operation of upgrading. f(a) — is a beauty of the number. tgcd[i] — gcd of all numbers on the prefix of length i. You can use function, which works in
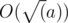 to calculate the beauty. Also you can make your solution more faster, it you will precalculate some small primes. Also you can use map < int, int > to store calculated values. DP base d[n][n] = curBeauty — is a current beauty of the array.
to calculate the beauty. Also you can make your solution more faster, it you will precalculate some small primes. Also you can use map < int, int > to store calculated values. DP base d[n][n] = curBeauty — is a current beauty of the array.
Second. Greedy. Let's find position r, which can upgrade our answer. If there some values of r — we will take most right position. We will add this position to the answer and upgrade our answer. Why it's correct? Let's fix an optimal solution (sequence of position, where we used an upgrading operation) r1 > r2 > ... > rk. Also we have an solution which was built by using greedy l1 > l2 > ... > lm. It's clear, that r1 ≤ l1, because all position with > l1 cannot upgrade anything (otherwise greedy will choose it as first position). In other hand, r1 ≥ l1, because otherwise we can upgrade in position l1 and make answer better. So, r1 = l1, and after that we can use our propositions for big indexes i.
402E - Strictly Positive Matrix / 403C - Strictly Positive Matrix
Let's look at the matrix a as a connectivity matrix of some graph with n vertices. Moreover, if aij > 0, then we have directed edge in the graph between nodes (i, j). Otherwise, if aij = 0 that graph does not contains directed edge between pair of nodes (i, j). Let b = ak. What does bij means? bij is the number of paths of length exactly k in our graph from vertex i to vertex j. Let pos is an integer, such that a[pos][pos] > 0. That is, we have a loop in the graph. So, if from the vertex pos achievable all other vertexes and vice versa, from all other vertices reachable vertex pos, then the answer is YES, otherwise the answer is NO. If reachability is missing, it is clear that for any k akipos = 0. If reachability there, we will be able to reach self-loop, use self-loop "to twist", and after that we will go to some another vertex.
403D - Beautiful Pairs of Numbers
First, we can note, that length of sequence is not greater then 50. Ok, but why? Because all numbers bi - ai are different, so 0 + 1 + ... + 50 > 1000. Let's imagine, that sequence from input is a sequence of non-intersecting segments. So, ci = bi - ai + 1 is length of segment i. Also, 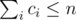 . After that let's calculate the following DP: d[i][j][k] — — number of sequences for which following holds: c1 < c2 < ... < ci, ci ≥ 1 , c1 + c2 + ... + ci = j and maximal number is less then k (upper bound of sequence). This DP will helps us to calculate number of ways to set length to each segment in sequence. It's simple to calculate such DP:
. After that let's calculate the following DP: d[i][j][k] — — number of sequences for which following holds: c1 < c2 < ... < ci, ci ≥ 1 , c1 + c2 + ... + ci = j and maximal number is less then k (upper bound of sequence). This DP will helps us to calculate number of ways to set length to each segment in sequence. It's simple to calculate such DP:
- base d[0][0][1] = 1,
- d[i][j][k + 1] = d[i][j][k + 1] + d[i][j][k] — we increase upper bound of sequence;
- d[i + 1][j + k][k + 1] = d[i + 1][j + k][k + 1] + d[i][j][k] — we are adding upper bound to the sequence.
We can calculate such DP, by using only O(N2) of memory, where N = 1000. After that we should multiply d[i][j][k] on i!, because we need number of sequences ci, where order does not matter.
After that we can calculate answer for n, k. Let's 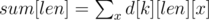 , where x — some upper bound of sequences. After that we should calculate next number: how many ways to set to distances between segments? It's clear, that we can increase distance between some segments, but we have only n - len such operations. It's well known, that answer number of ways equals to C(n - len + k, k). So, for each n we should sum by len following values: sum[len] * C(n - len + k, k).
, where x — some upper bound of sequences. After that we should calculate next number: how many ways to set to distances between segments? It's clear, that we can increase distance between some segments, but we have only n - len such operations. It's well known, that answer number of ways equals to C(n - len + k, k). So, for each n we should sum by len following values: sum[len] * C(n - len + k, k).
Note, that we need array C[n][k] (binomials) where n ≤ 2000, k ≤ 2000.
403E - Two Rooted Trees
First, for each vertex of the first and second tree we calculate two values in[s], out[s] — the entry time and exit time in dfs order from vertex with number 1. Also with each edge from both trees we will assosiate a pair (p, q), where p = min(in[u], in[v]), q = max(in[u], in[v]) (values in, out for each vertex we take from tree with another color). Now for each tree we will build two segment trees (yes, totally 4 segment trees). In first segment will store all pairs in following way: we will store a pair in node of segment tree if and only if (node of segment tree is a segment (l, r)) left element of pair lies in segment (l, r). In second segment tree we will store a pair if and only if right element of the pair lies in segment (l, r) All pairs in segment trees we will store in some order (in first segment tree — increasing order, in the second tree — decreasing order). Such trees use 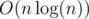 of memory, also you can build it in
of memory, also you can build it in 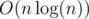 .
.
Good. How to answer on query (l, r) — erase all edges from tree for which exactly one vertex have value in[s] in segment (l, r)? We will go down in our segment tree. Let's imagine, that now we in some node of segment tree. Because we store all pairs in the first segment tree in increasing order of the right element, so answer to the query is a some suffix of the array of pairs. After we can add they to the answer (if it not erased yet). After that we should modify our segment tree: for each node, where we work with suffixes, we should erase all pairs from such suffix. So, this solution in 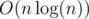 .
.
My solution to E: 6052738











After reading the tutorial my head started aching.
problem C is way easier than what they say, there is always a complete subgraph on the input (and it will always be i think, cause minimun number of edges is always 10 and vertex is always 5) so the 3rd condition (the tricky one) is always true, the other 2 conditions are met if you construct the graph with an O(N^2) algorithm. A good problem to think, but it is really easy to implement.
i tried implementing this approach during the contest, but got WA#3.
i think the reason is because for
n%5 != 0, u will have 2 or 3 extra edges to add. when these are added, it may result in the 2k + p condition being violated.weird, i got accepted in practice
For Div2 Problem C, why do you say that it is enough to prove that a graph is 0-connected or -3-connected? Can you further explain?
Ok, first for each subset holds: number edges ≤ 2k - 3, so if we will add p + 3 edges, following will holds: ≤ 2k + p
not sure about this, but i think he means where did this "magic" number
-3come from?Some months ago I've read about Laman graphs. So, - 3-interesting graph is a Laman graph.
after just having read up on Laman graphs, i have to say their interest value seems much greater than
-3! :Dfor problem 402E, will you assign a_ij = 1 if a_ij > 0? Otherwise b_ij isn't the number of paths of length k from i to j
You can imagine, that there are aij edges from i to j.
nvm got it
For problem D,I think d[i][j][k + 1] = d[i][j][k] + d[i][j][k] should be d[i][j][k + 1] = d[i][j][k+1] + d[i][j][k]
Problem D,Div 1 d[i][j][k] i<=50,j<=1000,k<=1000 tried to write the solution described in the tutorial but ofc I got MLE(50*1000*1000),where is my mistake,I think the constraints I wrote are correct.
You can see, that there is only transitions from d[i][j][k] to
So, you for each step i + 1 you need only values from i. So, you can reduce used memory.
Yes that's the way I got accepted,but anyways just saying...
For problem 403D could someone please tell me why the answer isn't sum[len] * ((k, n - len)) from Theorem 2?
Thank you!
On problem D div2, can i choose the same R multiple times ?
In problem c what is the meaning of p intersecting?
My solution for problem Div2 D is slightly different. Instead of updating all the indices, I just kept storing the last index which could improve the beauty. Take a look at my code for details. Please correct me if I am wrong. Could someone please explain to me why is my solution giving WA? http://codeforces.com/contest/402/submission/30985647 Thanks :)
could anyone explains 403E anymore?