| Codeforces Round 323 (Div. 1) |
|---|
| Finished |
→ Virtual participation
Virtual contest is a way to take part in past contest, as close as possible to participation on time. It is supported only ICPC mode for virtual contests.
If you've seen these problems, a virtual contest is not for you - solve these problems in the archive.
If you just want to solve some problem from a contest, a virtual contest is not for you - solve this problem in the archive.
Never use someone else's code, read the tutorials or communicate with other person during a virtual contest.
→ Problem tags
dp
math
number theory
*3300
No tag edit access
→ Contest materials
The problem statement has recently been changed. View the changes.
×
D. Number of Binominal Coefficients
time limit per test
4 secondsmemory limit per test
256 megabytesinput
standard inputoutput
standard outputFor a given prime integer p and integers α, A calculate the number of pairs of integers (n, k), such that 0 ≤ k ≤ n ≤ A and 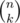 is divisible by pα.
is divisible by pα.
As the answer can be rather large, print the remainder of the answer moduly 109 + 7.
Let us remind you that 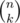 is the number of ways k objects can be chosen from the set of n objects.
is the number of ways k objects can be chosen from the set of n objects.
Input
The first line contains two integers, p and α (1 ≤ p, α ≤ 109, p is prime).
The second line contains the decimal record of integer A (0 ≤ A < 101000) without leading zeroes.
Output
In the single line print the answer to the problem.
Examples
Input
2 2
7
Output
3
Input
3 1
9
Output
17
Input
3 3
9
Output
0
Input
2 4
5000
Output
8576851
Note
In the first sample three binominal coefficients divisible by 4 are 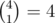 ,
, 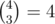 and
and 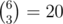 .
.
Codeforces (c) Copyright 2010-2024 Mike Mirzayanov
The only programming contests Web 2.0 platform
Server time: Apr/27/2024 12:13:35 (j1).
Desktop version, switch to mobile version.
Supported by
User lists


| Name |
|---|




