| Codeforces Round 395 (Div. 1) |
|---|
| Finished |
One of Timofey's birthday presents is a colourbook in a shape of an infinite plane. On the plane n rectangles with sides parallel to coordinate axes are situated. All sides of the rectangles have odd length. Rectangles cannot intersect, but they can touch each other.
Help Timofey to color his rectangles in 4 different colors in such a way that every two rectangles touching each other by side would have different color, or determine that it is impossible.
Two rectangles intersect if their intersection has positive area. Two rectangles touch by sides if there is a pair of sides such that their intersection has non-zero length
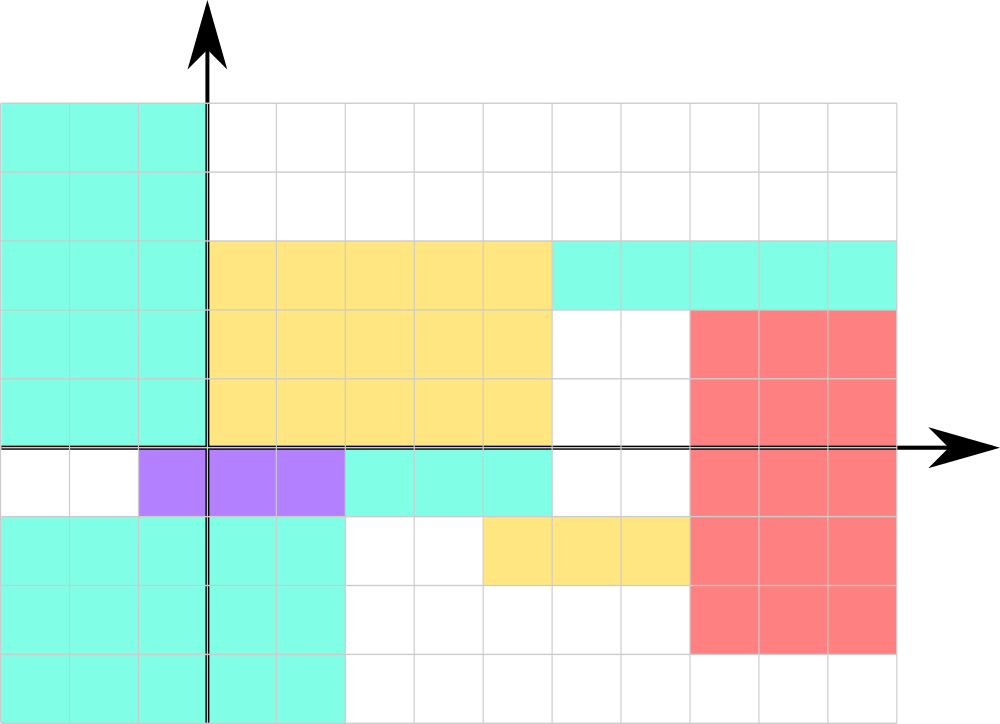 The picture corresponds to the first example
The picture corresponds to the first example The first line contains single integer n (1 ≤ n ≤ 5·105) — the number of rectangles.
n lines follow. The i-th of these lines contains four integers x1, y1, x2 and y2 ( - 109 ≤ x1 < x2 ≤ 109, - 109 ≤ y1 < y2 ≤ 109), that means that points (x1, y1) and (x2, y2) are the coordinates of two opposite corners of the i-th rectangle.
It is guaranteed, that all sides of the rectangles have odd lengths and rectangles don't intersect each other.
Print "NO" in the only line if it is impossible to color the rectangles in 4 different colors in such a way that every two rectangles touching each other by side would have different color.
Otherwise, print "YES" in the first line. Then print n lines, in the i-th of them print single integer ci (1 ≤ ci ≤ 4) — the color of i-th rectangle.
8
0 0 5 3
2 -1 5 0
-3 -4 2 -1
-1 -1 2 0
-3 0 0 5
5 2 10 3
7 -3 10 2
4 -2 7 -1
YES
1
2
2
3
2
2
4
1
| Name |
|---|




