Tutorial is loading...
Author: s17b2_voroneckij Development: s17b2_voroneckij
Tutorial is loading...
Author: akvasha Development: akvasha
Tutorial is loading...
Author: akvasha Development: akvasha , ilya_the_lamer
Tutorial is loading...
Author: ilya_the_lamer Development: ilya_the_lamer , akvasha
Tutorial is loading...
Author: platypus179 Development: platypus179
Tutorial is loading...
Author: platypus179 Development: platypus179
Tutorial is loading...
Author: KAN Development: platypus179 , ilya_the_lamer , akvasha











can someone please explain the problem statement of DIV 2 C more precisely?
I have a simpler solution. Take all edges that connect vertices of different colors. If all these edges have one common vertex — this vertex is the answer. Otherwise the answer is NO.
I'll definately look into your approach, but the problem itself is not clear to me. explanation to the sample inputs will do fine.
You have a tree and you must find such vertex v, that when you root the tree at the v, each subtree below v has one color (all vertices of subtree has the same color). Number of subtrees is equal to degree of v. The color of v doesn't matter at all.
Ok I got it now. Actually I missed the part "He doesn't consider the whole tree as a subtree since he can't see the color of the root vertex." :( and your approach is the simplest one I found so far. thanks
Your method is much simpler renadeen. Thoughtful insight.
See moejy0viiiiiv's solution.
You can check that by counting the number of edges with vertices of different colours. Also, count for each vertex how many such edges it is connected to. Since we must choose a vertex connected to all such edges, we just need to check whether there is some vertex that is connected a number of edges equal to the total number of such edges.
I solved it that way. In addition, if there is only one edge (u, v), the vertices of which are of different colors, then the answer can be either u or v
Hey! My solution is among the same lines but I am getting wrong answer. Any help is appreciated! Summary of submission: i) Remove same colored edges ii) If n==0 return any vertex iii) if n==1 return one of the vertices (u,v) iv) if n==2 , find the common vertex and if one doesn't exist return "NO" v) All the following edges have to have this common vertex in in Submission: https://codeforces.com/problemset/submission/763/69076469
I found my mistake. Accepted:)
Editorial for Div.2 D???
Sorry for this It's temporary mishap I'll fix it soon
Ready
Thanks for such great problems, I enjoyed from solving them :)
Can anybody expalin Div2 D please...
We may assume that our rectangles are drawn on an infinite sheet of squared paper. Divide it into squares 2 × 2 and mark the cells in each square by 1, 2, 3, 4 clockwise starting from the upper left corner. Since both sides of each rectangle are of odd length, its corner cells are marked by the same number. Let us number four different colors by 1, 2, 3, 4 and paint each rectangle with the color whose number marks the corner cells. It is readily seen that the numbers in the corners of any two adjacent rectangles are distinct.
the best
Better than editorial!
I got your solution but can you please explain the intuition behind it? This may seem silly but I really can't understand how did you come up with idea of making 2*2 square which is filled with 4 different colors?
This is not his idea.
In 2008 there was a mathematics olympiad: problems. The problem 5 from the olympiad is the same as problem Div2D.
He has copied the text from this editorial.
I tried to reverse engineer the possible thought process and I think it may have started from an observation of a simpler 1D problem.
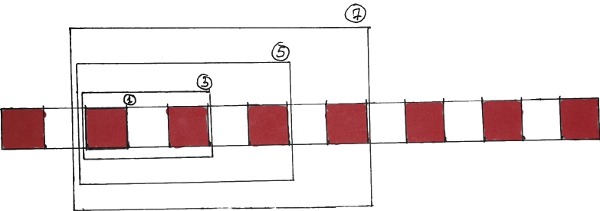
Observation 1. Rectangles of sizes 1, 3, 5, 7 that start with a
redsquare always end on theredsquare.Observation 2. After that you start to notice that the same is true for the rectangles that start with a
whitesquare.Observation 3. The 3rd observation is that all the possible rectangles are of these 2 types (i.e. there is no 3rd type of rectangle).
Observation 4. The last observation for 1D problem is that adjacent rectangles cannot be of the same type (i.e. they have to be of different types).
After that, probably, we could have generalized to 2D case, by seeing that in addition to already discovered 2 horizontal types (we were looking at horizontal line), there are now 2 more vertical types of rectangles. So, overall, there are 4 different types of rectangles and rectangles of the same type cannot be adjacent.
Thanks. Gotcha :)
Nice pixar
problem E can be solved in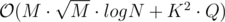 as well with MO's Algorithm + DSU with rollbacks and adding the border edges by brute.
as well with MO's Algorithm + DSU with rollbacks and adding the border edges by brute.
I tried hard but couldn't fit the time limit no matter what 24386929.
My complexity was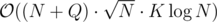 .
.
Could you elaborate how do I go down to your complexity?
sort the edges according to min of the two end points , now each query consists of edges from a range(all edges whose min endpoint is from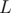 to
to  ) along with some edges whose endpoints are in the range
) along with some edges whose endpoints are in the range  to
to 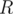 . you can get the answer for the edges in that range using MO's algo and add those few extra edges one by one and roll them back in the dsu later.
. you can get the answer for the edges in that range using MO's algo and add those few extra edges one by one and roll them back in the dsu later.
Oh.... So do you mean the Mo which never deletes anything and only adds new elements and rollbacks added?
Thank you
Div1E is very similar to this
We didn't want this solution to pass and made special anti-Mo cases, and as we see, no one who wrote Mo passed systest.
Forgive me if I misunderstand the whole situation, but for instance is the solution of saketh not using Mo's algorithm? In fact his code even has comment // mo's algorithm, and he did indeed pass system tests. Or are you referring to something else?
We tried to make all mo solutiobs get TL, but some did pass
763C — Тимофей и перемодулирование Sorry for stupid question,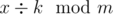
How it calculated??
This is right:
x % k mod (m) == x*k1 mod m, where k1*k == 1 mod m ==> k1 == k^(m-2) mod m??http://e-maxx.ru/algo/reverse_element
Please give some more explanation for Div-2 D.
Since sides of all rectangles are parallel to x and y axis only there can not be 4 or more rectangles which touch each other therefore solution always exists. Now since side lengths are odd therefore one of x1 or x2 is odd and other is even same goes for y (one can check by drawing in x,y plane) . For rectangles with x1 odd, since its x2(end) is even its neighbors will always have there x1(start) as even (they cannot have same color) and the same goes for y.Therefore 4 possible combinations are possible for x,y -> odd,odd even,odd odd,even and even,even. Hence the solution.
Thanks bro. Got it. Nice Explanation.
for div 2 C , wont the given editorial give a time complexity of O(n^2).... if each vertice is coloured differently, then it will do dfs from each of the vertice ...? or i understood the solution incorrectly.. B-)
No, the answer will have complexity of O(n).
There can be more than one edge connecting different coloured vertices eg. 1->2->3 and c[i] is same as vertices number , then we can hold by two...similarly if there were many coloured vertices ,I would have to dfs it those many times according to the editorial....atleast that's what I understood ☺☺
You only need to check the two end vertices from one such edge. If non of these vertices is the solution, then no solution exists and you can abort.
I can't understand how to promise that a subtree doesn't annoy him if there are vertices of same color in it, please explain this sample: 4 1 2 2 4 4 3 1 1 3 2 YES 4 But in 4's subtree, the color of 3 and the color of 1 or 2 are different
Take a look at this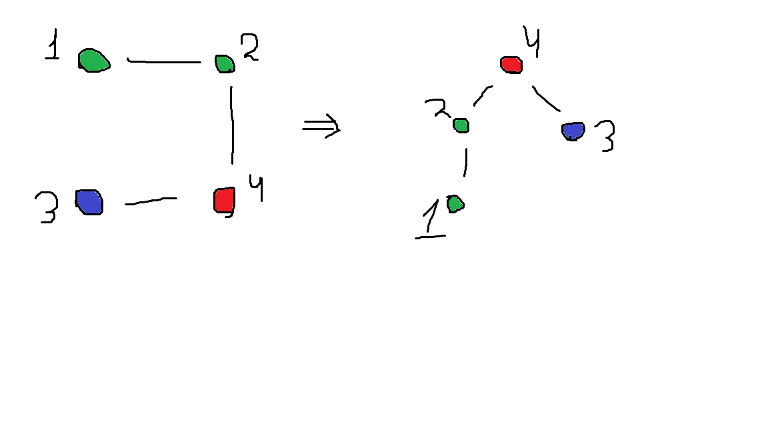 Problem says that root node doesn't belong to any subtree.
Problem says that root node doesn't belong to any subtree.
Also subtrees that are going from root node can have different colors.
problem C Does it really necessary to solve it in two case? when we choose some element y,then we check if y-d,y-2d,...,y-kd belongs to A until it not or k=n-1.Then,the same,check y+d,y+2d,....,y+kd.Because what we check is continous,it's "safe" and easy to find the value of the first element.
Can you explain how to choose the value of y and d? Thank you.
well,just as the solution above said,choose some two elements a and b,assume x=a-b,and count the number of such pair which has the same difference value,assume it's k(including (a,b)),then we get d=x/(n-k).
Edit: got it!
Hello!I have replied the question in the first page,I hope you can have a look at it please.
Sorry to bother you, but I wanna know why the 2D structure like this, please explain it, thank you.
Consider a rectangle,we have know that rectangles cannot intersect,and all sides of the rectangles have odd length.As we all know,the Four color theorem,so it must have a solution.What we need to do is to find a solution to give a color to every rectangle.If the lower left quarter of the rectangle,(x1,y1),so that we can know the situation of (x1+odd,x2+odd),we can confirm that we just need to color the rectangle according to its x1 and y1's parity.
I hope my solution and explanation would help you!
Can someone explain 763C more elaborately? I am unable to understand it.
See
763C is the E question of Div 2. You have given the link for C question of Div 2.
Div1.C Please explain why we consider the case 2*n>m? I don't understand
Note that an arithmetic progression of m terms are all distinct mod m if we have (d,m)=1. So if the given set forms an arithmetic progression, so does the complement of it.
But why the method when 2n<m can't be used when 2n>m?
Edit:Nevermind, I figured it out when I started writing the code.
I noticed that I misunderstood your point, thanks to Ismll. :) So let me answer your question again: If we do not consider the case when 2*n>m, the following statement is not true.
On the other hand, x must be difference of exactly n - k + 1 pairs of elements of A. (Actually, I think that this should be n-k)
This is due to somewhat number theoretic reason. It is like, let me say, an overflow mod m. For example, let x = 3*d (i.e. k=3), n = m-2. The pair (s, s+(n-1)d) should not be counted, but it is counted since s = s+(n+2)d mod m. However if 2*n<m, this does not happen.
More precisely, we should consider the size relation between 2n-3 and m, rather than 2n. As jo_on put it above, overflow mod m may happen in some situation. In fact, the boundary condition is that the sum of the two largest differences(in absolute value) of element pairs equals to m*d. That is pairs (s,s+(n-1)d) and (s,s+(n-2)d), whose sum of differences is (2n-3)d.So we should consider the size relation between 2n-3 and m. Once 2n-3<m, the insecurity, namely overflow mod m won't happen.
In short, when 2n-1=m, the case must be safe.In practice, whether 2n or 2n-3, both of them can get accepted.
Ps: My AC code with 2n 24488586 and 2n-3 24491759.
My algorithm for Div. 2 C was exactly the same.
Can anyone give an easier-to-understand explanation for Div1-C? I still don't understand how to deal with modulo m operation.
Weak cases in Div2C
4
1 2
2 3
3 4
5 3 2 4
My AC code gives YES but correct one is NO
From a problemsetting perspective, I'd like to ask ilya_the_lamer about how you wrote a checker for this problem, and how this affected the system testing.
By the way, writing the checker surely seems harder than the original problem, and I'm assuming you wrote a n log n (take all the rectangles of some color, do horizontal/vertical segments independently, check for overlap). I wonder how running O(n log n) for n=500000 on ~50 test cases for a bunch of programs affected this system testing. It seemed pretty fast to me, just curious how it ran so fast in this way!
We used 2 scanlines to build graph, and then just simply checked, that there is no edges with same-colored vertexes. As you correctly mentioned, this works in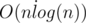 .
.
I can share you checker, if you are really interested in it.
What about fast working, most of the solutions, that used wrong idea, didn't pass small pretests (n near 100), so testing on big tests didn't even start in most cases.
Although I couldn't submit it during the competition (and honestly it took to long to code to be practical for myself), I have a very different number theoretical approach to 763C - Timofey and remoduling. The problem is effectively to find
xanddsuch that{a[0],a[1],...a[n-1]} = {x,x+d,...x+(n-1)d} (mod m). We solve this using the sum and sum of squares to create a quadratic equation of eitherxord, confirm the existence of a solution with the Legendre symbol and use Cipolla's algorithm to find the solutions if they exist. There are at most two, which we can confirm inO(n log n).In order to meet the conditions for which this algorithm can work, we consider only
mwhich is odd andn<m-1. While there is no deterministic way for solving an arbitrary quadratic equation, it can easily be transformed intoy^2 = k (mod m)where the Cipolla algorithm allows us to solve with approximately1/2probability for each random number. So, the expected value is 2. The overall complexity isO(n log n + k log m), wherekis the number of tries in the Cipolla algorithm. It can be quite high for the problem conditions, so although there is a probability for failure, it is very small.Submission: 24420260
Nice solution! And in fact, you can simply try all a[i]-a[1] as d and find x with x+(x+d)+...+(x+(n-1)d) equals to the sum of the elements. As you have said, there are at most two pairs (x,d) which satisfy x^2+(x+d)^2+...+(x+(n-1)d)^2 equals to the sum of square. So we can check these two pairs by brute force.
Wow. I actually realized we can easily reduce the candidates for
dton-1candidates without additional calculations but I didn't think to use that in conjunction to this approach. This approach has a far simpler implementation.May I ask why you said that "There are at most two"?
Assume there is a solution y which is not x ≡ y or x ≡ - y. Then p|x2 - y2 = (x + y)(x - y) is not possible as (x + y, p) = 1 and (x - y, p) = 1. More generally the number of solutions of a modular n-th order polynomial equation is bounded by n (Lagrange's theorem).
Can somebody please explain Div 1C? I am unable to understand the solution.
Regarding Div1 B about coloring rectangles: is there any reasonable way to solve the problem just by looking at the connectivity graph and not by taking advantage of odd side lengths?
Btw. this problem is genius IMO, thanks ilya_the_lamer!
I'm almost sure there should be one. Indeed, four color theorem guarantees that the solution exists. Moreover, I remember that the only case that needs 4 colors is kind of pathological, so for this case you only need 3 colors. Finally, what I think can be done is go line per line (in the sense x-coordinate by x-coordinate) and color all the rectangles that pass through this x-coordinate alternatively.
Actually you do need 4 colors here :) Counter-example with 6 rectangles: 1 rectangle in the center 5 other rectangles linked in a cycle (of odd=5 length) each of which touches center rectangle
763E — Timofey and our friends animals
aren't we storing O(N) values?
hoping not to say something stupid: let be f(n) the number of node needed by a segment tree with lenght n f(1) is clearly 1; //himself f(n) = 1 + f(floor(n/2)) + f(ceil(n/2)); //himself + left son + right son
we can simply prove that this lead us to f(n) = 2n-1;
if i didn't understand, can you please explain me why? thanks
Model solution provided in editorial gets AC; at the same time it is not clear to me how segment gluing is being done there, and for example on test
it says 0 :)
P.S. And I also started to believe that a nice O(N*K*K) solution works here as well (like 24603977), but this one gives 2 for
In Div2E/Div1C, I don't understand the following statement:
"On the other hand, we have that n is less then m/2, so x must be difference of exactly n - k + 1 pairs of elements of A."
Formally, why the following holds?
Can someone please look into issue for Div1 E Timofey and our friends animals: http://codeforces.com/blog/entry/52419
In Div2 E Timofey and remoduling, I think author's solution code is wrong It can't answer for this simple input. 8 3 0 6 7 Results should be 6 1 but author's code stucks in somewhere.
oh, m was prime number. my mistake.
For Prob Div2C Just have a look at my code it's pretty simple and clear. https://codeforces.com/contest/763/submission/89345877
I dont know if anyone has solved Div1 A (763A) this way or not. (The concept is root changing)
I just took the root as 1 intially and checked if it is possible for that root to have a value by checking (No. of subtree nodes)*(value of one of the immediate child of the root)==(sum of the values in the subtree), If not then shift the roots.
For better understanding you can check my solution here.
Solution by the method explained