| VK Cup 2018 - Round 2 |
|---|
| Finished |
Arkady decides to observe a river for n consecutive days. The river's water level on each day is equal to some real value.
Arkady goes to the riverside each day and makes a mark on the side of the channel at the height of the water level, but if it coincides with a mark made before, no new mark is created. The water does not wash the marks away. Arkady writes down the number of marks strictly above the water level each day, on the i-th day this value is equal to mi.
Define di as the number of marks strictly under the water level on the i-th day. You are to find out the minimum possible sum of di over all days. There are no marks on the channel before the first day.
The first line contains a single positive integer n (1 ≤ n ≤ 105) — the number of days.
The second line contains n space-separated integers m1, m2, ..., mn (0 ≤ mi < i) — the number of marks strictly above the water on each day.
Output one single integer — the minimum possible sum of the number of marks strictly below the water level among all days.
6
0 1 0 3 0 2
6
5
0 1 2 1 2
1
5
0 1 1 2 2
0
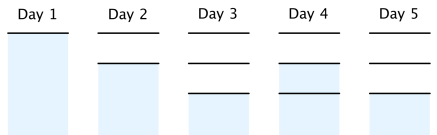
In the first example, the following figure shows an optimal case.

Note that on day 3, a new mark should be created because if not, there cannot be 3 marks above water on day 4. The total number of marks underwater is 0 + 0 + 2 + 0 + 3 + 1 = 6.
In the second example, the following figure shows an optimal case.
| Name |
|---|




