You are given a set of n elements indexed from 1 to n. The weight of i-th element is wi. The weight of some subset of a given set is denoted as 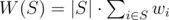 . The weight of some partition R of a given set into k subsets is
. The weight of some partition R of a given set into k subsets is 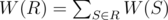 (recall that a partition of a given set is a set of its subsets such that every element of the given set belongs to exactly one subset in partition).
(recall that a partition of a given set is a set of its subsets such that every element of the given set belongs to exactly one subset in partition).
Calculate the sum of weights of all partitions of a given set into exactly k non-empty subsets, and print it modulo 109 + 7. Two partitions are considered different iff there exist two elements x and y such that they belong to the same set in one of the partitions, and to different sets in another partition.
The first line contains two integers n and k (1 ≤ k ≤ n ≤ 2·105) — the number of elements and the number of subsets in each partition, respectively.
The second line contains n integers wi (1 ≤ wi ≤ 109)— weights of elements of the set.
Print one integer — the sum of weights of all partitions of a given set into k non-empty subsets, taken modulo 109 + 7.
4 2
2 3 2 3
160
5 2
1 2 3 4 5
645
Possible partitions in the first sample:
- {{1, 2, 3}, {4}}, W(R) = 3·(w1 + w2 + w3) + 1·w4 = 24;
- {{1, 2, 4}, {3}}, W(R) = 26;
- {{1, 3, 4}, {2}}, W(R) = 24;
- {{1, 2}, {3, 4}}, W(R) = 2·(w1 + w2) + 2·(w3 + w4) = 20;
- {{1, 3}, {2, 4}}, W(R) = 20;
- {{1, 4}, {2, 3}}, W(R) = 20;
- {{1}, {2, 3, 4}}, W(R) = 26;
Possible partitions in the second sample:
- {{1, 2, 3, 4}, {5}}, W(R) = 45;
- {{1, 2, 3, 5}, {4}}, W(R) = 48;
- {{1, 2, 4, 5}, {3}}, W(R) = 51;
- {{1, 3, 4, 5}, {2}}, W(R) = 54;
- {{2, 3, 4, 5}, {1}}, W(R) = 57;
- {{1, 2, 3}, {4, 5}}, W(R) = 36;
- {{1, 2, 4}, {3, 5}}, W(R) = 37;
- {{1, 2, 5}, {3, 4}}, W(R) = 38;
- {{1, 3, 4}, {2, 5}}, W(R) = 38;
- {{1, 3, 5}, {2, 4}}, W(R) = 39;
- {{1, 4, 5}, {2, 3}}, W(R) = 40;
- {{2, 3, 4}, {1, 5}}, W(R) = 39;
- {{2, 3, 5}, {1, 4}}, W(R) = 40;
- {{2, 4, 5}, {1, 3}}, W(R) = 41;
- {{3, 4, 5}, {1, 2}}, W(R) = 42.
| Name |
|---|




