Editorial
Tutorial is loading...
Solution (Vovuh)
#include <bits/stdc++.h>
using namespace std;
int main() {
#ifdef _DEBUG
freopen("input.txt", "r", stdin);
// freopen("output.txt", "w", stdout);
#endif
int n, m;
cin >> n >> m;
vector<int> cnt(n);
for (int i = 0; i < m; ++i) {
int col;
cin >> col;
++cnt[col - 1];
}
cout << *min_element(cnt.begin(), cnt.end()) << endl;
return 0;
}
Editorial
Tutorial is loading...
Solution (Vovuh)
#include <bits/stdc++.h>
using namespace std;
int main() {
#ifdef _DEBUG
freopen("input.txt", "r", stdin);
// freopen("output.txt", "w", stdout);
#endif
int n, k;
scanf("%d %d", &n, &k);
vector<int> a(n);
vector<int> t(n);
int overall = 0;
for (int i = 0; i < n; ++i)
scanf("%d", &a[i]);
for (int i = 0; i < n; ++i)
scanf("%d", &t[i]);
vector<int> pr(n);
for (int i = 0; i < n; ++i) {
if (i) pr[i] += pr[i - 1];
if (t[i] == 0) pr[i] += a[i];
else overall += a[i];
}
int add = 0;
for (int i = k - 1; i < n; ++i)
add = max(add, pr[i] - (i >= k ? pr[i - k] : 0));
printf("%d\n", overall + add);
return 0;
}
Editorial
Tutorial is loading...
Solution (Ajosteen)
#include <bits/stdc++.h>
using namespace std;
const int N = 109;
int n;
string a[4][N];
int main() {
cin >> n;
for(int k = 0; k < 4; ++k)
for(int i = 0; i < n; ++i){
cin >> a[k][i];
for(int j = 0; j < n; ++j)
a[k][i][j] -= '0';
}
vector <int> v;
for(int k = 0; k < 4; ++k){
int sum = 0;
for(int i = 0; i < n; ++i)
for(int j = 0; j < n; ++j)
if((i + j) % 2 != a[k][i][j])
++sum;
v.push_back(sum);
}
int res = int(1e9);
vector <int> perm;
for(int k = 0; k < 4; ++k) perm.push_back(k);
do{
int sum = 0;
for(int k = 0; k < 4; ++k){
int id = perm[k];
if(k & 1)
sum += v[id];
else
sum += n * n - v[id];
}
res = min(res, sum);
}while(next_permutation(perm.begin(), perm.end()));
cout << res << endl;
}
Editorial
Tutorial is loading...
Solution (adedalic)
#include <bits/stdc++.h>
#define fore(i, l, r) for(int i = int(l); i < int(r); i++)
#define all(a) (a).begin(), (a).end()
#define sz(a) int(a.size())
#define mp make_pair
#define x first
#define y second
using namespace std;
typedef long long li;
typedef pair<int, int> pt;
inline pt operator -(const pt &a, const pt &b) {
return {a.x - b.x, a.y - b.y};
}
inline li cross(const pt &a, const pt &b) {
return a.x * 1ll * b.y - a.y * 1ll * b.x;
}
const int N = 200 * 1000 + 555;
int n;
pt p[N];
inline bool read() {
if(!(cin >> n))
return false;
fore(i, 0, n)
scanf("%d%d", &p[i].x, &p[i].y);
return true;
}
bool used[N];
bool check() {
int i1 = -1, i2 = -1;
fore(i, 0, n) {
if(used[i])
continue;
if(i1 == -1)
i1 = i;
else if(i2 == -1)
i2 = i;
}
if(i2 == -1)
return true;
fore(i, 0, n) {
if(used[i])
continue;
if(cross(p[i2] - p[i1], p[i] - p[i1]) != 0)
return false;
}
return true;
}
bool check2(pt a, pt b) {
memset(used, 0, sizeof used);
fore(i, 0, n)
if(cross(b - a, p[i] - a) == 0)
used[i] = 1;
return check();
}
inline void solve() {
if(n <= 2) {
puts("YES");
return;
}
if(check2(p[0], p[1]) || check2(p[0], p[2]) || check2(p[1], p[2]))
puts("YES");
else
puts("NO");
}
int main(){
if(read()) {
solve();
}
return 0;
}
Editorial
Tutorial is loading...
Solution (Ajosteen)
#include <bits/stdc++.h>
using namespace std;
const int N = 200 * 1000 + 9;
int n;
int a[N];
int f[N];
vector <int> v[N];
void upd(int pos, int d){
for(; pos < N; pos |= pos + 1)
f[pos] += d;
}
int get(int pos){
int res = 0;
for(; pos >= 0; pos = (pos & (pos + 1)) - 1)
res += f[pos];
return res;
}
int main() {
scanf("%d", &n);
for(int i = 0; i < n; ++i){
scanf("%d", a + i);
--a[i];
}
for(int i = 0; i < n; ++i){
if(a[i] < N)
v[a[i]].push_back(i);
upd(i, 1);
}
long long res = 0;
for(int i = 0; i < n; ++i){
int to = min(N - 1, a[i]);
res += get(to);
for(auto x : v[i])
upd(x, -1);
}
for(int i = 0; i < n; ++i)
if(i <= a[i])
--res;
assert(res % 2 == 0);
cout << res / 2 << endl;
}
Editorial
Tutorial is loading...
Alternative solution (jtnydv25)
Solution (adedalic, suffix array)
#include <bits/stdc++.h>
#define fore(i, l, r) for(int i = int(l); i < int(r); i++)
#define all(a) (a).begin(), (a).end()
#define sz(a) int(a.size())
#define mp make_pair
#define x first
#define y second
using namespace std;
typedef pair<int, int> pt;
const int LOGN = 21;
const int N = 1000 * 1000 + 555;
int n;
string s;
inline bool read() {
if(!(cin >> n))
return false;
char buf[N];
assert(scanf("%s", buf) == 1);
s = buf;
return true;
}
pair<pt, int> d[N], curP[N];
int szd = 0;
int cnt[N], szcnt;
int rdp[N];
inline void radix_sort() {
fore(k, 0, 2) {
szcnt = 0;
fore(i, 0, szd) {
int val = k == 0 ? d[i].x.y : d[i].x.x;
while(szcnt <= val)
cnt[szcnt++] = 0;
cnt[val]++;
}
int sum = 0;
fore(i, 0, szcnt) {
rdp[i] = sum;
sum += cnt[i];
}
fore(i, 0, szd) {
int val = k == 0 ? d[i].x.y : d[i].x.x;
curP[rdp[val]++] = d[i];
}
fore(i, 0, szd)
d[i] = curP[i];
}
}
int c[N], id[N];
int lcp[N];
int lg[N];
int st[LOGN][N];
void precalc() {
s += '$';
for(int len = 1; len < 2 * sz(s); len <<= 1) {
szd = 0;
fore(i, 0, sz(s)) {
int sh = len >> 1;
d[szd++] = {len == 1 ? mp((int)s[i], 0) : mp(c[i], c[(i + sh) % sz(s)]), i};
}
radix_sort();
c[d[0].y] = 0;
fore(i, 1, szd)
c[d[i].y] = c[d[i - 1].y] + (d[i - 1].x != d[i].x);
if(c[d[szd - 1].y] == sz(s) - 1)
break;
}
fore(i, 0, sz(s)) {
c[i]--;
if(c[i] >= 0) id[c[i]] = i;
}
s.pop_back();
int l = 0;
fore(i1, 0, n) {
l = max(l - 1, 0);
if(c[i1] == n - 1)
continue;
int i2 = id[c[i1] + 1];
while(i1 + l < n && i2 + l < n && s[i1 + l] == s[i2 + l])
l++;
lcp[c[i1]] = l;
}
lg[0] = 0;
fore(i, 1, N) {
lg[i] = lg[i - 1];
if((1 << (lg[i] + 1)) <= i)
lg[i]++;
}
fore(pw, 0, LOGN) {
if(pw == 0) {
fore(i, 0, n)
st[pw][i] = lcp[i];
continue;
}
fore(i, 0, n) {
st[pw][i] = st[pw - 1][i];
if(i + (1 << (pw - 1)) < n)
st[pw][i] = min(st[pw][i], st[pw - 1][i + (1 << (pw - 1))]);
}
}
}
inline int getMin(int l, int r) {
if(l >= r) swap(l, r);
int len = lg[r - l];
return min(st[len][l], st[len][r - (1 << len)]);
}
inline bool eq(int i1, int i2, int l) {
if(i1 == i2) return true;
return getMin(c[i1], c[i2]) >= l;
}
int l[N], mx[N];
inline void solve() {
precalc();
fore(i, 0, n / 2) {
int c1 = i, c2 = n - 1 - i;
if(s[c1] != s[c2]) {
l[i] = -1;
continue;
}
int lf = 0, rg = min(c1, n - 1 - c2) + 1;
while(rg - lf > 1) {
int mid = (lf + rg) >> 1;
if(eq(c1 - mid, c2 - mid, 2 * mid + 1))
lf = mid;
else
rg = mid;
}
l[i] = lf;
}
fore(i, 0, n / 2) {
if(l[i] < 0)
continue;
mx[i - l[i]] = max(mx[i - l[i]], 2 * l[i] + 1);
}
fore(i, 1, n / 2)
mx[i] = max(mx[i], mx[i - 1] - 2);
fore(i, 0, (n + 1) / 2) {
if(i) printf(" ");
printf("%d", mx[i] == 0 ? -1 : mx[i]);
}
puts("");
}
int main(){
if(read()) {
solve();
}
return 0;
}
Solution (adedalic, hashes)
#include <bits/stdc++.h>
#define fore(i, l, r) for(int i = int(l); i < int(r); i++)
#define all(a) (a).begin(), (a).end()
#define sz(a) int(a.size())
#define mp make_pair
#define x first
#define y second
using namespace std;
typedef long long li;
const li MOD = li(1e18) + 3;
const li BASE = 1009;
inline li norm(li a) {
while(a >= MOD)
a -= MOD;
while(a < 0)
a += MOD;
return a;
}
inline li mul(li a, li b) {
li m = ((long double)(a) * b) / MOD;
return norm(a * b - m * MOD);
}
const int N = 1000 * 1000 + 555;
int n;
string s;
inline bool read() {
if(!(cin >> n))
return false;
char buf[N];
assert(scanf("%s", buf) == 1);
s = buf;
return true;
}
li h[N], pw[N];
inline void precalc() {
h[0] = 0;
fore(i, 0, n)
h[i + 1] = norm(mul(h[i], BASE) + s[i] - 'a' + 1);
pw[0] = 1;
fore(i, 1, N)
pw[i] = mul(pw[i - 1], BASE);
}
inline li getHash(int l, int r) {
return norm(h[r] - mul(h[l], pw[r - l]));
}
inline bool eq(int i1, int i2, int l) {
if(i1 == i2) return true;
return getHash(i1, i1 + l) == getHash(i2, i2 + l);
}
int l[N], mx[N];
inline void solve() {
precalc();
fore(i, 0, n / 2) {
int c1 = i, c2 = n - 1 - i;
if(s[c1] != s[c2]) {
l[i] = -1;
continue;
}
int lf = 0, rg = min(c1, n - 1 - c2) + 1;
while(rg - lf > 1) {
int mid = (lf + rg) >> 1;
if(eq(c1 - mid, c2 - mid, 2 * mid + 1))
lf = mid;
else
rg = mid;
}
l[i] = lf;
}
fore(i, 0, n / 2) {
if(l[i] < 0)
continue;
mx[i - l[i]] = max(mx[i - l[i]], 2 * l[i] + 1);
}
fore(i, 1, n / 2)
mx[i] = max(mx[i], mx[i - 1] - 2);
fore(i, 0, (n + 1) / 2) {
if(i) printf(" ");
if(mx[i] == 0) mx[i] = -1;
printf("%d", mx[i]);
}
puts("");
}
int main(){
if(read()) {
solve();
}
return 0;
}
Editorial
Tutorial is loading...
Solution (adedalic)
#include <bits/stdc++.h>
using namespace std;
#define fore(i, l, r) for(int i = int(l); i < int(r); i++)
#define forn(i, n) fore(i, 0, n)
const int MOD = int(1e9) + 7;
inline int norm(int a) {
while(a >= MOD)
a -= MOD;
while(a < 0)
a += MOD;
return a;
}
inline int mul(int a, int b) {
return int((a * 1ll * b) % MOD);
}
inline int binPow(int a, int k) {
int ans = 1;
while(k > 0) {
if(k & 1) ans = mul(ans, a);
a = mul(a, a);
k >>= 1;
}
return ans;
}
const int N = 200 * 1000 + 555;
int f[N], inf[N];
void precalc() {
f[0] = inf[0] = 1;
fore(i, 1, N) {
f[i] = mul(f[i - 1], i);
inf[i] = mul(inf[i - 1], binPow(i, MOD - 2));
}
}
int n, k, w[N];
inline bool read() {
if(!(cin >> n >> k))
return false;
forn(i, n)
cin >> w[i];
return true;
}
inline int c(int n, int k) {
if(k > n || n < 0) return 0;
if(k == 0 || n == k) return 1;
return mul(f[n], mul(inf[n - k], inf[k]));
}
inline int s(int n, int k) {
if(n == 0) return k == 0;
if(k == 0) return n == 0;
int ans = 0, sg[2] = {1, MOD - 1};
forn(cnt, k)
ans = norm(ans + mul(sg[cnt & 1], mul(c(k, cnt), binPow(k - cnt, n))));
return mul(ans, inf[k]);
}
inline void solve() {
int sum = 0;
forn(i, n)
sum = norm(sum + w[i]);
int s0 = s(n, k);
int s1 = mul(n - 1, s(n - 1, k));
cout << mul(sum, norm(s0 + s1)) << endl;
}
int main() {
#ifdef _DEBUG
freopen("input.txt", "r", stdin);
#endif
precalc();
assert(read());
solve();
#ifdef _DEBUG
cerr << "TIME = " << clock() << endl;
#endif
return 0;
}










Damn, I used Order Statistics tree to solve Problem E after the contest, and now I find it can be done with BIT.
http://codeforces.com/contest/961/submission/36984273
Can you explain your approach ?
nice problemset :)
Had solved E in 3 hours by using persistence segment tree. By seeing the editorial i think that i know nothing :)
Nice editorial!
I solved E with persistence segment tree too, but it didn't took too much time because the only difference between normal segment tree and persistence segment tree is that you have to change the update process of later.
It's beautiful problemset, thx!
Geomety always seems to get me..
Can someone give me more detailed explanation of question B?
First, in O(N) time, we can calculate "total", the current total number of theorems that Mishka will be able to write without the secret technique.
Now we calculate the EXTRA number of theorems (apart from the ones for which Mishka needs no help) that Mishka will be able to write if the secret technique will get used at the first minute; this is O(K) of course. Call this number "cumu". Now in O(1) time, we can find out the number of theorems that Mishka can write down if the secret technique will get used at the second minute (just remove the number of theorems for the first minute (if applicable) and add the number of theorems for the (K+1)th minute (if applicable)). Keep "sliding" till you reach the end. Of course, maintain a maximum of what you have seen so far, which we call maxcumu.
Finally, add "maxcumu" to "total". http://codeforces.com/contest/961/submission/36992860
I used just the priority queue and AVL for E and it just worked fine. In min priority queue I save pair of (ai,i). On reaching i+1 I pop all those ai from priority queue where aj<i+1 (j<=i) because they can't pair with further seasons. Now I need to find those indices which are in priority queue and are less than a(i+1) because if index is greater than a(i+1) it won't be able to pair with season(i+1). For doing this I use an AVL. Whenever I am popping from priority queue I delete the corresponding index from AVL. I then count all indices lesser than (ai+1) and it to my final answer. Then finally I insert the pair (a[i+1],i+1) to priority queue and index i+1 to AVL. (Both operations take LogN complexity). It was much easier to code and code for AVL is easily available on GFG. My Solution
I have made the same, but with Fenwick tree (BIT), much more simple to code.
Nice F
Amazing problemset. I solved E after the contest using merge sort tree, it was pretty intuitive, and good oportunity to learn to code merge sort tree (because i didnt implement it before, only knew idea). Anyone else solved it this way?
Yah ! I also sloved it using merge sort tree.
Can anyone help me in understanding Problem E?
Observe that for some season i we'll only get a collision with an episode of season j where j < i if aj >= i and ai >= j. So we just need to able to answer for a particular season i how many seasons with index j such that j < i have aj >= i and ai >= j. We can do this query for all i (using a merge-sort tree for example) and then report the answer.
For E, just use BIT to maintain sorted segments. Then use binary search (
lower_boundin C++) to get the answer in each segment. I think it's the most simplest approach (or the best answer especially in a time highly limited competition).Here is my code 36971807
Most of the shortest answers are done by this way.
Could you elaborate on your method? Looks interesting
Well. In this problem, we need to calculate how many numbers are greater than i in the range [i + 1, a[i]].
Let d[l, r, x] denote how many numbers are greater than x in the range [l, r].
Obviously, d[l, r, x] = d[1, r, x]-d[1, l-1, x] (prefix sums)
Then you can use Binary Indexed Tree (BIT) with vector, which means each node of the BIT is a vector that collects numbers in a range, just like the node of a typical BIT sums numbers in the range.
After sorting each vector, you can use binary search to get answers in each vector. By using BIT query method, you can form prefix sums and get d[l, r, x].
What will be the complexity of this solution? Like if You sort vectors in every node of BIT? Won't it be too much? Further, what will be the max size of a any vector representing a node?
Each number appears in O(log n) vectors. So the space complexity is O(n log n). Time complexity is O(n log^2 n).
Well, the max size of a vector is O(n). However, the average size of vectors is just O(log n).
nice approach :)
For problem D what would be the approach if maximum number of lines allowed were 3?
This is one thing I could think of; I am sure we can do better. Assume n >= 4, and assume that the n points lie on 3 lines. Consider any four points (say, the first ten points given). By Pigeonhole Principle, some 2 points lie on the same line. And well, take all cases. Once you are done finding one of the lines, the problem reduces to the given problem.
Another less "casework" way considers n>= 10. Consider the first 10 points. Again by Pigeonhole Principle, some 4 points lie on the same line, and (I guess) we can also prove that if four points are collinear, then one of the lines must pass through them. So just find a quadruple of points that are collinear. If there does not exist a quadruple, then our assumption is false, otherwise the quadruple determines one line, and the problem has been reduced to D.
Another solution which can be easily generalized for more than two lines is: pick two different points at random, remove them and all points collinear with them and repeat until you have drawn expected number lines, and repeat the whole process until you have found way to partition all of the points or until clock() < TIME_LIMIT * CLOCKS_PER_SEC. Suppose pn points lie on first line and qn on the second (p + q) = 1 then probability of choosing points lying on the same line is roughly p2 + q2 which is greater or equal to ). In case of 3 lines we have at least
). In case of 3 lines we have at least  chance for our first guess and at least
chance for our first guess and at least  for our second guess. which is total
for our second guess. which is total  (or for k lines
(or for k lines 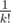 ). For k ≤ 5 this should be enough.
). For k ≤ 5 this should be enough.
But the random can be hacked in open hacking……like 36960802
It can't be if I seed random number generator with the hash of the input. Or at least hacking it would be much more difficult.
Can anyone help me in understanding Problem c?i am not getting tutorial too.
We have 4 pieces of board so to make a new chessboard out of the 4 we need 2 pieces with black cell on the (0,0) position and 2 pieces with white cell on the (0,0) position. Also note that once we know the color of (0,0) position we can make the whole chessboard out of it. So we find the cost of converting each piece into two chessboards — one with white cell at (0,0) and another with black cell at (0,0) and then we calculate the minimum of all possible ways.
My solution
Just wanted to mention that F is essentially the same (actually more explicit) as an old POI problem: https://main.edu.pl/en/archive/oi/19/pre
How to solve problem D for N points and K lines?
Something about Problem G. I guess most of us get the formula below easily:
But the Editorial above claims:
So may anybody prove that:
I would gladly hear the formal proof of equation myself since it doesn't sound like easy transformation.
Here is a proof I thought of. Also, sorry for too many revisions :P
Consider n students who wish to participate in a contest. They must enter themselves in exactly k non-empty groups. One of these groups is a special group who gets to participate in Div 1, while the others participate in Div 2. Furthermore, Alice, one of the students, is very good at coding, so she will always participate in Div 1. Furthermore, the special group has a team leader. We count the number of ways C of partitioning the students in two ways.
First, we select, out of n - 1 students, j - 1 students who, along with Alice, form the special group. This can be done in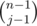 ways. Now the n - j normal students can be partitioned in
ways. Now the n - j normal students can be partitioned in 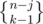 ways, and the team leader of the special group can be chosen in j ways. Thus
ways, and the team leader of the special group can be chosen in j ways. Thus 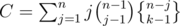 .
.
Another way is this: Suppose Alice is the team leader. Then simply partition the n students into k groups in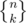 ways, and the team Alice belongs to is special. Otherwise choose a team leader out of the remaining students in n - 1 ways (call this chosen leader Bob), and partition the n - 1 students other than Bob in
ways, and the team Alice belongs to is special. Otherwise choose a team leader out of the remaining students in n - 1 ways (call this chosen leader Bob), and partition the n - 1 students other than Bob in 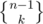 ways. The one Alice belongs to is the special group, so Bob belongs to that group of course. Therefore
ways. The one Alice belongs to is the special group, so Bob belongs to that group of course. Therefore 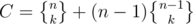 .
.
Yes, you are right, but you make exactly what problem G asks. Your proof is just a more formal than from editorial. In other words, formulas are same because they count same thing.
What I (and probably, Blue233333) expected are just formal equivalent transformations of left and right parts using some properties of Binomial Coefficients and Stirling numbers.
With swm_sxt and zsnuo's help, I find an approach to use equivalent transformations to prove that, but I am still a little confused.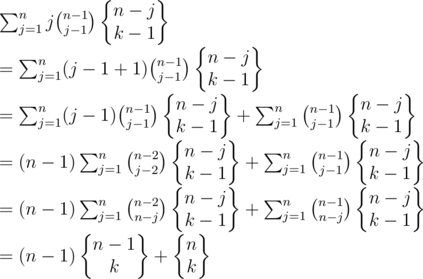
However, I don't understand the last step's formula transformations very clearly, while I could only understand it with this: Dividing n people into k non-empty groups, means that we first choose j, 0 ≤ j ≤ n - 1, people to be members of person n's group, and then divide the remained persons into k - 1 groups.
You can check it at wikipedia.
There are n circles drawn on a piece of paper in such a way that any two circles intersect in two points, and no three circles pass through the same point. Turbo the snail slides along the circles in the following fashion. Initially he moves on one of the circles in clockwise direction. Turbo always keeps sliding along the current circle until he reaches an intersection with another circle. Then he continues his journey on this new circle and also changes the direction of moving, i.e. from clockwise to anticlockwise or vice versa. Suppose that Turbo’s path entirely covers all circles. Prove that n must be odd.
This is from IMO. Also, it is unrelated.
can someone please explain me F. I didn't get the editorial :(
Here is my blog post on the very elegant geometry problem D :)
i feel like my brain expanded after solving E xD
I would like to share my solution for problem F.
Given a string s let's create a new string t of double size concatenating the first character with the last character, the second with the penultimate, and so on.. For example, given
abababwe gotabbaabbaabbaIf you look carefully at this new string, we are now interested in palindromes! (convince yourself about this). Of course, we are not interested in all palindromes but some of them. More precisely we are interested in the palindromes that meet these requirements (Let L be the beginning of the palindrome, R the end, and n the length of the original string):
Lis an even positionRis an odd positionLis in the first half of the string (this is because is symmetric)(R-L+1)/2is odd (this is a requirement of the problem)n-R/2-1 > L/2(is not a proper prefix-suffix)So we can iterate over all the biggest palindromes and then just calculate the answer for each substring and propagate the answer to small ones.
The solution is O(N);
Here is the link to my submission
I realise this is an old contest but I'm just trying it now. Is test case 34 on F some sort of anti-hashing hack? I tried a polynomial rolling hash with three different (prime) values for x, all working mod 2^64, and they all fail on this case (here, here and here). When I changed the modulus to 10^9+7, it passed, even though this gives a far smaller range of possible hash values.
I somehow happened to solve a problem in this round, to notice your comment :)
The case looks to be the famous one: https://codeforces.com/blog/entry/4898. In short, the polynomial is something like $$$(1 - x) (1 - x^2) (1 - x^4) (1 - x^8) \cdots$$$ and any odd $$$x$$$ makes it divisible by $$$2^{64}$$$. For a prime modulus, we can have a probability bound from the fact that a non-zero polynomial of degree $$$n$$$ has at most $$$n$$$ roots (Schwartz–Zippel lemma).
Thanks, I learned something new.
I had a problem with D, test case 49 seems YES to me but the wanted answer is NO. All the points lie in the same line.
All the lines passing throw $$$p[i]$$$ and $$$p[0]$$$ (where $$$1 \le i \le 5$$$) are with the exact same slope $$$1.61803398875$$$.
Link to the plot and slopes calculation
My submission: 172444322
The solution passed when I got rid of all double in the code. What I learned here is to think about doubles as monsters that will eat so I have to run away.
The link for the alternative solution of problem F is broken. Here's the link: https://codeforces.com/blog/entry/58707?#comment-423461
209797912 where am i going wrong could anyone help me get over it, its getting failed in 5th test case Assign a[i]=-1*a[i] if t[i]=0 and then find minimum sum subarray of length k and store the starting idx of that subarray then storing idx to idx+k-1 in set then adding all the remaining elements to res if a[i]>0 or if i exist in st (abs(a[i])