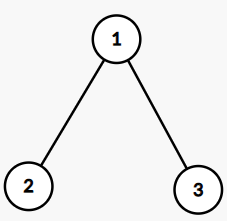
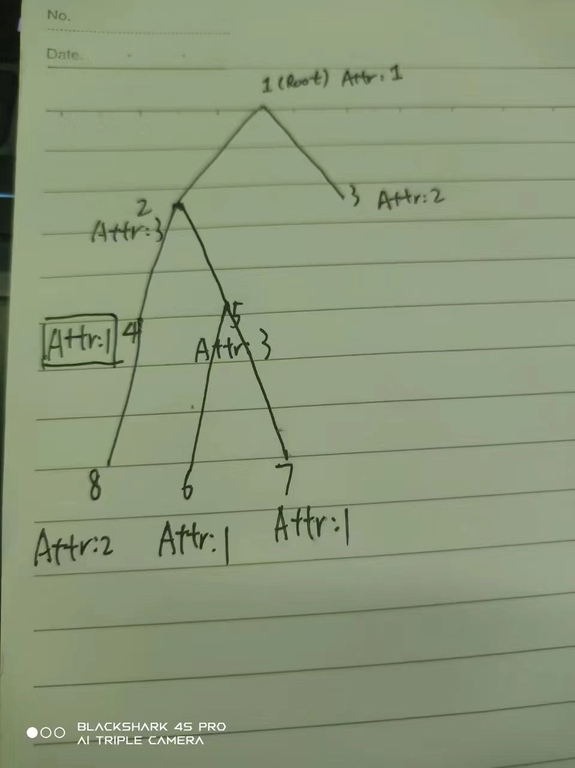
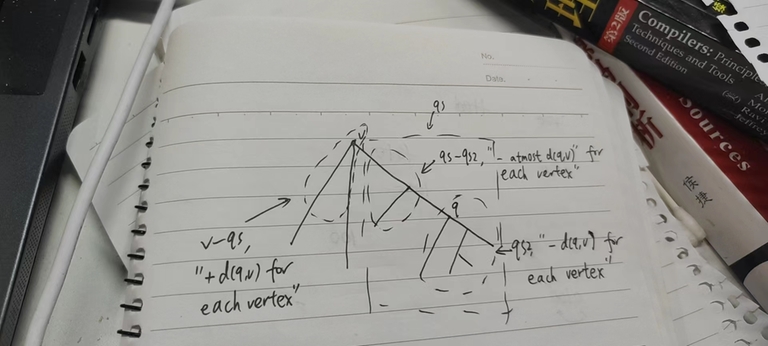
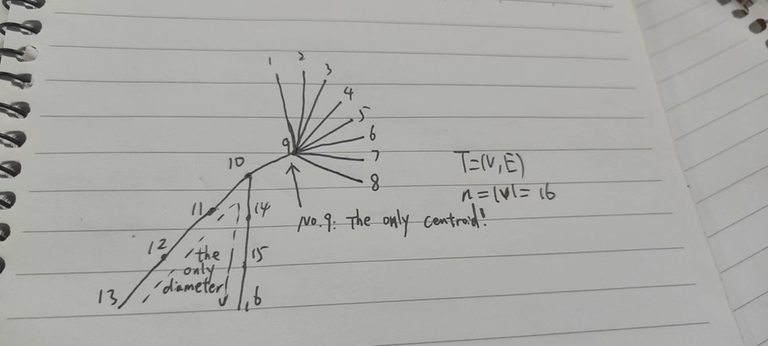
You just deleted my grandson dfsof's blog and banned him for 48 hours. Is CF a dictator? I hate dictators. Which rule did he violate, did you just ban him because he "offended" some admins?

Some top coders want to close dfsof's blog on MathStackExchange. Fortunately, MSE is democratic, after voting, the blog is still alive and gets some upvotes. Well, it is his first blog on PE, I never expected so many unpleasant issues to happen.

If CF is a dictator, I respect you. If CF only values top coders, I think at least I should quit.

MikeMirzayanov

You are given $$$n$$$ '2' and $$$m$$$ '3'. Try to concatenate these $$$n+m$$$ characters into a largest base-10 number $$$d$$$ such that $$$2023 \mid d$$$. If you cannot get such $$$d$$$, print $$$-1$$$.

Example $$$1$$$:

Input: $$$n = 2, m = 8$$$.

Output: $$$d = 2233333333$$$. Please note that $$$2233333333 = 2023 \times 1103971$$$, and it is the largest.

Example $$$2$$$:

Input: $$$n = 2, m = 2$$$.

Output: $$$-1$$$ (no solution).

Constraints: $$$1 \leq n,m \leq 1e6$$$. Time $$$1s$$$, memory $$$256MB$$$.

Link: https://ac.nowcoder.com/acm/contest/56458/E

Alice and Bob are playing a game on a tree $$$T$$$ whose root is $$$1$$$. $$$T$$$ has $$$n$$$ vertices and $$$n-1$$$ edges, each vertex $$$v$$$ has an attribute $$$a \in \{1,2,3\}$$$. If $$$a=1$$$, a person on $$$v$$$ must jump to the parent of $$$v$$$, i.e., v->parent. If $$$a=2$$$, a person on $$$v$$$ must jump to $$$v$$$'s grandparent, i.e., v->parent->parent. If $$$a=3$$$, a person on $$$v$$$ can either jump to v->parent or v->parent->parent. Alice starts the first and she can choose a leaf node of $$$T$$$ to start. If somebody cannot make a move, she/he loses the game. For example, if Alice stands on a child of the root and this child has attribute $$$2$$$, then Alice loses as this child does not have a grandparent. Similarly, if Bob stands on the root $$$1$$$, he will lose as he cannot move no matter what the attribute of the root is.

Input contains $$$n+1$$$ ($$$2 \leq n \leq 10^5$$$) lines.

The first line contains a single integer $$$n$$$, the number of vertices.

The second line contains $$$n$$$ integers $$$a_i$$$ ($$$1 \leq a_i \leq 3$$$) representing the attribute of each vertex $$$i$$$.

The following $$$n-1$$$ lines representing edges, each line contains two integers $$$u_i$$$ and $$$v_i$$$. $$$u_i$$$-$$$v_i$$$ is an undirected edge of $$$T$$$.

Output should contain $$$n-1$$$ lines, each line is a query. The $$$i$$$-th ($$$1 \leq i \leq n-1$$$) line represents the winner if Alice and Bob plays optimally when the $$$i$$$-th edge is deleted from $$$T$$$. The deletion operations are independent along queries, i.e., the $$$i$$$-th edge is recovered from deletion when you process the $$$i+1$$$-th query. Note that Alice can only choose the original leaves of $$$T$$$ as the start vertex even if the deletion operation results in new leaves.

Test case 1:

Input:

3

1 2 1

1 2

1 3

Output:

Alice

Bob

In the first line, the first edge, i.e., $$$1-2$$$ is destroyed. In this case, Alice can choose to start from vertex $$$3$$$, and jump to vertex $$$1$$$. Then, Bob will get stuck at vertex $$$1$$$. Alice wins.

In the second line, the first edge $$$1-2$$$ is recovered and the second edge $$$1-3$$$ is destroyed. Here, $$$3$$$ becomes an isolation vertex. If Alice starts at $$$3$$$, she cannot jump. If Alice starts at $$$2$$$, she cannot jump either as $$$2$$$ does not have grandparent. The parent of $$$2$$$ is the root $$$1$$$ but $$$1$$$ does not have a parent. Therefore, no matter where Alice starts, Bob will win.

Test case 2:

8

1 3 2 1 3 1 1 2

1 2

1 3

2 4

2 5

4 8

5 6

5 7

Output:

Alice

Bob

Bob

Alice

Bob

Bob

Bob

For example, if you delete the first edge $$$1-2$$$, Alice will win if she chooses to start at $$$8$$$.

If you delete the fourth edge $$$2-5$$$, Alice will win if she chooses to start at $$$6$$$ or $$$7$$$.

If you delete the second edge $$$1-3$$$, Bob will win. For example, if Alice choose to start at $$$7$$$, she will jump to $$$5$$$ and Bob jumps to $$$1$$$.

Notes:

(1) Constraint: $$$2 \leq n \leq 10^5$$$.

(2) There are $$$n-1$$$ queries and the deletion operations in queries are independent.

(3) Alice can only choose the original leaves of $$$T$$$ as the start vertex. Deleting an edge will result in new leaves, for example, if you delete edge $$$4-8$$$ in the second test case, $$$4$$$ becomes a new leaf but Alice cannot start from it.

(4) Neither Alice nor Bob can move across the root $$$1$$$. For example in the first test case, Alice cannot moves from $$$2$$$ to $$$3$$$ along $$$2-1-3$$$.

Given an one-indexed array with $$$n$$$ pairwise distinct elements, find the number of pairs $$$(l, r)$$$ ($$$1 \leq l \leq r \leq n$$$) such that the inversion number of $$$(a[l], a[l+1], ..., a[r])$$$ is odd. $$$(a[l], a[l+1], ..., a[r])$$$ is a continuous subarray of $$$a$$$ that starts from $$$l$$$ and ends at $$$r$$$ (both inclusive).

For example, $$$a=[3, 2, 1]$$$, the answer is $$$3$$$: $$$(1, 2), (2, 3), (1, 3)$$$.

We have $$$n$$$ closed intervals. Find a set of intervals with maximum cardinality such that the intervals in this set intersect pairwise.

As far as I know, we can use the famous greedy algorithm to solve the maximum interval independent set problem, i.e., the interval scheduling problem. But how about the maximum interval clique problem? We can convert it into an interval graph which is also chordal, and find the maximum clique using LexBFS in $$$O(n^2)$$$ time as the number of edges in the interval graph is $$$O(n^2)$$$. What about an $$$O(nlog^kn)$$$ algorithm? Am I overthinking?

Nowcoder problem (Chinese) link. The submission is private because I don't want to publish my Nowcoder account, but you can copy the code at the end of this blog and paste it to the answer sheet, it will get AC.

English version

First I would like to thank ShaoNianTongXue5307 for his idea!

This is a learning note, most for myself. Most of this blog is not original.

Part 1: Problem Statement:

A tree $$$T=(V, E)$$$ has $$$n$$$ vertices and $$$n-1$$$ edges, the weight of each vertex $$$i$$$ is $$$a_i$$$.

For each edge $$$e$$$, you can determine its direction, i.e., for two vertices $$$u, v$$$, there are two states: $$$u \rightarrow v$$$ and $$$v \rightarrow u$$$. There are $$$2^{n-1}$$$ states in total.

For each state $$$S$$$, we define $$$f(S)$$$ as

$$$f(S) := \sum\limits_{(u, v) \in V \times V, v\,\text{is reachable from}\,u} |a_u - a_v|$$$.

Compute the sum of $$$f(S)$$$ over all $$$2^{n-1}$$$ states $$$S$$$, modulo $$$998244353$$$.

Example:

Suppose $$$n=3$$$, and two edges connect $$$(1, 2), (2, 3)$$$, respectively. $$$a_1 = 3, a_2 = 1, a_3 = 2$$$, the answer is $$$14$$$.

Constraints: $$$2 \leq n \leq 2 \cdot 10^5$$$, $$$1 \leq a_i \leq 10^9$$$.

Part 2: What is the centroid decomposition good at?

Before we learn centroid decomposition, we should first know what it is good at. For a tree $$$T = (V, E)$$$, we can decompose $$$V$$$ into $$$V = V_1 \cup V_2 \cup ... \cup V_t$$$, where $$$V_i (1 \leq i \leq t)$$$ are pairwise disjoint non-empty sets. $$$V_1$$$ is a singleton which contains only one element: The centroid. $$$V_2, ..., V_t$$$ are the connected components of $$$T \setminus V_1$$$. We want to calculate some function $$$f(T)$$$, and we assume that the base case, where $$$V(T) = 1$$$, is easy to calculate. This assumption is not strict, because if we can't even deal with the case where $$$V(T)=1$$$, we can actually achieve nothing. The another important function besides $$$f$$$ is the merge function: $$$merge(V_1, V_2, ..., V_t)$$$. Formally

$$$f(V) = \sum\limits_{i=1}^t f(V_i) + merge(V_1, V_2, ..., V_t)$$$. (1)

Like the merge sort, the number of iterations in the centroid decomposition algorithm is $$$O(log |V|)$$$, so it takes roughly $$$O(log |V| \cdot merge)$$$ time. Therefore, the most important advantage to use centroid decomposition is that the merge function could be computed fast enough. Otherwise, it is even slower than the brute force! In our solution merge is $$$O(|V|log|V|)$$$ so its complexity is $$$O(|V|log^2|V|)$$$. You may recall the process of the merge sort if you have trouble understanding these words.

Part 3: What is a centroid, and what is a centroid decomposition?

For a tree, the vertex $$$v$$$ is called a centroid if and only if any subtree rooted at $$$v$$$'s child has a size at most half the size of the original tree. For example, the centroids for the path A--B--C--D are B and C.

Property $$$1$$$: A tree has one or two centroids.

Proof: First, we prove that one tree has at least one centroid. The centroid could be found using a constructive algorithm. First we specify an original root $$$r$$$. Initialize $$$v$$$ as $$$r$$$. Check whether $$$v$$$ is a centroid. If yes, we have already done. If not, replace $$$v$$$ with $$$v$$$'s heavy child $$$u$$$, i.e., $$$argmax(u)\{size[u] \mid u\,\text{is}\,v\text{'s child}\}$$$. The iteration will terminate since the size is finite. When it terminates, the size of subtrees rooted at $$$v$$$'s children $$$\leq \frac{|V|}{2}$$$. We need to be careful that, when the tree is rooted at $$$v$$$ (instead of $$$r$$$), the parent of $$$v$$$ in the $$$r$$$-rooted tree becomes a child of $$$v$$$ in the $$$v$$$-rooted tree, so we need to check the parent of $$$v$$$ in the $$$r$$$-rooted tree. Since the algorithm does not terminate at $$$v$$$'s parent, the size of $$$v \leq \frac{|V|}{2}$$$, therefore, (the size of $$$v$$$'s parent) — (the size of $$$v$$$) $$$\leq \frac{|V|}{2}$$$, which also satisfies the condition.

Second, we prove that one tree has at most two centroids. Suppose $$$a$$$ and $$$b$$$ are two centroids. Then, there is a subtree of $$$a$$$'s child ($$$A$$$) containing $$$b$$$, and a subtree of $$$b$$$'s child ($$$B$$$) containing $$$a$$$, $$$A \cup B = V, |A|, |B| \leq \frac{|V|}{2}$$$. By the principle of inclusion-exclusion (PIE), $$$A$$$ and $$$B$$$ must be disjoint, therefore there is an edge $$$ab$$$. So there cannot be $$$\geq 3$$$ centroids, and if it contains $$$2$$$ centroids, these two centroids must be adjacent.

Property $$$2$$$: $$$v := argmin(v)\{max\{size[u] \mid u\,\text{is}\,v\text{'s child in the tree rooted at }v\}\}$$$ is a centroid. This can be proved using the fact that every tree has at least one centroid, so the "best" vertex must be a centroid. In English, for a vertex $$$v$$$, lets the score of $$$v$$$ be the maximum size of subtrees rooted at $$$v$$$'s children in the $$$v$$$-rooted tree. The $$$v$$$ with the minimum score is the centroid.

For example, the edges are $$$(A, B), (B, D), (B, C), (C, E)$$$. The scores of $$$A,B,C,D,E$$$ are $$$4, 2, 3, 4, 4$$$ respectively, so the centroid is $$$B$$$.

Property $$$3$$$: $$$v$$$ is a centroid if and only if for arbitrary $$$q \in V$$$, $$$\sum\limits_{u \in V} d(u, v) \leq \sum\limits_{u \in V} d(u, q)$$$.

Proof: $$$\rightarrow$$$: $$$v$$$ is a centroid. Let's $$$qs$$$ be the size of subtree of $$$v$$$'s child that contains $$$q$$$. For the $$$qs2$$$ part (the subtree rooted at $$$q$$$), each vertex decreases $$$d(q, v)$$$, for the $$$|V|-qs$$$ part, each vertex increases $$$d(q, v)$$$, and for the $$$qs-qs2$$$ part, we don't know exactly, but each of vertex decreases at most $$$d(q, v)$$$ (if $$$qs > qs2$$$, the upper bound of total decrease $$$(qs-qs2)d(q, v)$$$ cannot be achieved), so the general distance sum increases when $$$v$$$ moves to $$$q$$$ as $$$qs \leq \frac{|V|}{2}$$$ by the definition of the centroid.

$$$\leftarrow$$$: If $$$qs > qs2$$$, then the $$$qs-qs2$$$ part decreases strictly less then $$$(qs-qs2) \cdot d(q, v)$$$, and the $$$qs$$$ part decreases strictly less then $$$qs \cdot d(q, v) \leq (|V| - qs) \cdot d(q, v)$$$. Therefore, $$$qs = qs2 = \frac{|V|}{2}$$$. There fore $$$q$$$ and $$$v$$$ are adjacent, the size of subtree rooted at $$$v$$$ in a $$$q$$$-rooted tree is $$$\frac{|V|}{2}$$$, therefore $$$q$$$ is a centroid.

Property $$$4$$$: Suppose $$$v$$$ is a centroid of the original tree $$$T$$$. If one leaf node is added to or deleted from $$$T$$$, then there is a centroid of $$$T$$$ (after operation) among $$$\{v\} \cup N(v)$$$, where $$$N(v)$$$ is the neighbor of $$$v$$$. Simply speaking, if $$$v$$$ is not a centroid after adding that leaf, we can replace $$$v$$$ with one of $$$v$$$'s child whose subtree contains that leaf. If $$$v$$$ is not a centroid after deleting that leaf, we can replace $$$v$$$ with $$$v$$$'s heavy child.

Counterexample $$$1$$$: The diameter may not pass the centroid.

Somebody thinks the diameter must pass the centroid. That is wrong! The diameter may not pass the centroid.

Centroid decomposition is a recursion process. Just find one centroid of the tree (if there are two centroid, find an arbitrary one of it), delete the centroid and the edges connecting to it. After that, the tree is decomposed into several connected components. Then, we do such decomposition for every connected component. Stop the recursion process if the vertex set of the tree is a singleton. Since each iteration halves the size, the centroid decomposition takes at most $$$O(log|V|)$$$ rounds.

Code: My code is adapted from this blog by lingfunny. It can AC ABC291EX Balanced Tree, submission is here. I paste the core code here:

struct cdt{
    const int cdtINF = 0x7fffffff;
    int *mxsz, *sz, *p, rt, nm;
    //sz(x): The size of x
    //mxsz(x): max{sz(y)|y is a child of x}
    //p parent
    bool* vis; //for convenience, we don't use a bitset here. But we can!
    std::vector<int>* g;
 
    cdt(int n):rt(0), nm(n){
        assert(n > 0);
        mxsz = new int[n+1];
        mxsz[0] = cdtINF;
        sz = new int[n+1];
        p = new int[n+1];
        g = new std::vector<int>[n+1];
        vis = new bool[n+1];
        memset(vis, 0, (n+1)*sizeof(bool));
    }
 
    ~cdt(){
        delete[] mxsz;
        delete[] sz;
        delete[] p;
        delete[] g;
        delete[] vis;
    }
 
    void addedge(int u, int v){
        g[u].push_back(v);
        g[v].push_back(u);
    }
 
    void calcsize(int u, int fa){
        mxsz[u] = sz[u] = 1;
        for(int v: g[u]){
            if(!vis[v] && v != fa){
                calcsize(v, u);
                sz[u] += sz[v];
                mxsz[u] = std::max(mxsz[u], sz[v]);
            }
        }
        mxsz[u] = std::max(mxsz[u], nm-sz[u]);
        //mxsz最小的一定是树的重心, 因为一棵树至少有一个重心, 可能有1个或2个重心
        //The argmin mxsz has to be the centroid, because one tree has at least one centroid!
        if(mxsz[u] <= mxsz[rt]) rt = u;
    }
 
    void operate(int u, int fa){
        calcsize(u, -1), calcsize(rt, -1), p[rt] = fa, dfz(rt);
    }
 
    void dfz(int u){
        vis[u] = 1;
        for(int v: g[u]){
            if(!vis[v]){
                nm = sz[v], rt = 0;
                operate(v, u);
            }
        }
    }
};

int main(void){
    int n;
    cin >> n;
    cdt c(n); 
    for(int i = 1, u, v; i <= n; ++i){
        cin >> u >> v;
        c.addedge(u, v);
    }
    c.operate(1, -1);
}

This code is a little bit comprehensive. It contains three recursions: operate, calcsize and dfz. It starts with operate, operate will call calcsize and dfz. calcsize will call itself and dfz will call operate in turn. The calcsize function is easier to understand, it has two usage: Calculate the size of each subtree, and find the centroid. Note that we call calcsize twice in the operation function, that is quite necessary: In the first call, we find the centroid, and in the second call, we find the size of each connected components. Then, the operation function calls the dfz function. In the initial call of dfz, i.e., the call from operation rather than the call from dfz itself, the parameter int u is guaranteed to be a centroid, so it recursively removes this centroid $$$V_1$$$ and decomposes $$$T \setminus V_1$$$ into connected components $$$V_2, V_3, ..., V_t$$$. The father (parent) of the centroids of $$$V_2$$$, $$$V_3$$$, ..., $$$V_t$$$ are all $$$V_1$$$, this is achieved using p[rt] = fa. There is no merge (described in the Part 2) operations in the code above. If there is a merge operation, we should place it at the end of the dfz function.

This is a graph from Xing-Ling's blog. $$$1$$$ is the centroid of the original tree. If we cut $$$1$$$, we get two connected components: $$$\{2,3,4,5,6\}$$$ and $$$\{7,8,9,10,11\}$$$. The centroids of these two connected components are $$$2$$$ and $$$7$$$ respectively, so the fathers (parents) of $$$2$$$ and $$$7$$$ are both $$$1$$$. Then we do the centroid decomposition in each component...

Part 4: Back to the original problem: How should we write the merge function?

This part is similar to the EATROCK from CodeChef Starter80A. The original Nowcoder problem is much harder than this CodeChef problem, only $$$8$$$ participants solve it.

In the merge function, we only consider $$$u$$$ and $$$v$$$ are from the different components in each iteration. In this case, $$$d(u, v) = dep(u) + dep(v)$$$, where $$$dep(\cdot)$$$ denotes the depth of $$$\cdot$$$ in the current tree. For $$$u$$$ and $$$v$$$ from different components, if $$$v$$$ is reachable from $$$u$$$, then $$$d(u, v) = dep(u) + dep(v)$$$ edges have to be fixed, so there are $$$n - dep(u) - dep(v) - 1$$$ free edges. So each $$$(u, v)$$$ pair appears $$$2^{n - dep(u) - dep(v) - 1}$$$ times, contributing $$$2^{n - dep(u) - dep(v) - 1}|a_u - a_v|$$$ to the final answer. The total contribution in each decomposition iteration is

$$$2^n \sum\limits_{a_v \leq a_u} (a_u - a_v)2^{-dep(u)-dep(v)} = 2^n (\sum\limits_{u} a_u2^{-dep(u)}(\sum\limits_{v, a_v \leq a_u}2^{-dep(v)}) - \sum\limits_{u}2^{-dep(u)}(\sum\limits_{v, a_v \leq a_u}a_v2^{-dep(v)}))$$$ (2).

Then, we can implement the merge by sorting $$$a$$$ and maintaining two prefix sums: $$$\sum\limits_{v} a_v2^{-dep(v)}$$$ and $$$\sum\limits_{v} 2^{-dep(v)}$$$. The complexity is $$$O(|V|log|V|)$$$ for each iteration because the sorting is a bottleneck. The overall complxity is $$$O(|V|log^2|V|)$$$ with a slightly larger constant, but the nowcoder machine is really fxxking fast. Code (645ms):

#include <bits/stdc++.h>

#pragma GCC optimize("Ofast,unroll-loops")
#pragma GCC target("avx2,tune=native")

//jiangly Codeforces
constexpr int P = 998244353;
using i64 = long long;
// assume -P <= x < 2P
int norm(int x) {
    if (x < 0) {
        x += P;
    }
    if (x >= P) {
        x -= P;
    }
    return x;
}
template<class T>
T power(T a, i64 b) {
    T res = 1;
    for (; b; b /= 2, a *= a) {
        if (b % 2) {
            res *= a;
        }
    }
    return res;
}
struct Z {
    int x;
    Z(int x = 0) : x(norm(x)) {}
    Z(i64 x) : x(norm((int)(x % P))) {}
    int val() const {
        return x;
    }
    Z operator-() const {
        return Z(norm(P - x));
    }
    Z inv() const {
        assert(x != 0);
        return power(*this, P - 2);
    }
    Z &operator*=(const Z &rhs) {
        x = i64(x) * rhs.x % P;
        return *this;
    }
    Z &operator+=(const Z &rhs) {
        x = norm(x + rhs.x);
        return *this;
    }
    Z &operator-=(const Z &rhs) {
        x = norm(x - rhs.x);
        return *this;
    }
    Z &operator/=(const Z &rhs) {
        return *this *= rhs.inv();
    }
    friend Z operator*(const Z &lhs, const Z &rhs) {
        Z res = lhs;
        res *= rhs;
        return res;
    }
    friend Z operator+(const Z &lhs, const Z &rhs) {
        Z res = lhs;
        res += rhs;
        return res;
    }
    friend Z operator-(const Z &lhs, const Z &rhs) {
        Z res = lhs;
        res -= rhs;
        return res;
    }
    friend Z operator/(const Z &lhs, const Z &rhs) {
        Z res = lhs;
        res /= rhs;
        return res;
    }
    friend std::istream &operator>>(std::istream &is, Z &a) {
        i64 v;
        is >> v;
        a = Z(v);
        return is;
    }
    friend std::ostream &operator<<(std::ostream &os, const Z &a) {
        return os << a.val();
    }
};

#define C 200005
int a[C];
Z finalans = 0;
Z p2[C], p2inv[C];
Z all1, all2;
std::vector<Z> curtag1(C), curtag2(C);

struct cdt{
    const int cdtINF = 0x7fffffff;
    int *mxsz, *sz, *p, rt, nm;
    //sz(x): The size of x
    //mxsz(x): max{sz(y)|y is a child of x}
    //p parent
    bool* vis; //for convenience, we don't use a bitset here. But we can!
    std::vector<int>* g;
    //aifrom = ai + from. 
    //element[0]: a[i].
    //element[1]: Which tree it belongs to.
    //element[2]: The depth, i.e., the distance between this element to the centroid

    cdt(int n):rt(0), nm(n){
        assert(n > 0);
        mxsz = new int[n+1];
        mxsz[0] = cdtINF;
        sz = new int[n+1];
        p = new int[n+1];
        g = new std::vector<int>[n+1];
        vis = new bool[n+1];
        memset(vis, 0, (n+1)*sizeof(bool));
    }

    ~cdt(){
        delete[] mxsz;
        delete[] sz;
        delete[] p;
        delete[] g;
        delete[] vis;
    }

    void addedge(int u, int v){
        g[u].push_back(v);
        g[v].push_back(u);
    }

    void calcsize(int u, int fa, int tag, int depth, std::vector<std::array<int, 4>>* aifrom){
        mxsz[u] = sz[u] = 1;
        if(aifrom){
            aifrom->push_back(std::array<int, 4>{a[u], tag, depth, u});
        }
        for(int v: g[u]){
            if(!vis[v] && v != fa){
                calcsize(v, u, tag, depth+1, aifrom);
                sz[u] += sz[v];
                mxsz[u] = std::max(mxsz[u], sz[v]);
            }
        }
        mxsz[u] = std::max(mxsz[u], nm-sz[u]);
        //mxsz最小的一定是树的重心, 因为一棵树至少有一个重心, 可能有1个或2个重心
        //The argmin mxsz has to be the centroid, because one tree has at least one centroid!
        if(mxsz[u] <= mxsz[rt]) rt = u;
    }

    void operate(int u, int fa, std::vector<std::array<int, 4>>* aifrom){
        //tag: Note which subtree, i.e., which connected component u belongs to after the centroid decomposition!
        calcsize(u, -1, u, 1, aifrom), calcsize(rt, -1, u, 1, nullptr), p[rt] = fa;
        dfz(rt);
    }

    void dfz(int u){
        vis[u] = 1;
        std::vector<std::array<int, 4>> aifrom;
        aifrom.push_back(std::array<int, 4>{a[u], 0, 0, u});
        for(int v: g[u]){
            if(!vis[v]){
                nm = sz[v], rt = 0;
                operate(v, u, &aifrom);
            }
        }
        std::sort(aifrom.begin(), aifrom.end());
        all1 = 0, all2 = 0;
        for(int i = 0; i < aifrom.size(); ++i){
            curtag1[aifrom[i][1]] = 0;
            curtag2[aifrom[i][1]] = 0;
        }
        Z tmp = 0; //The tmp in unnecessary. It helps me debug.
        for(int i = 0; i < aifrom.size(); ++i){
            int tag = aifrom[i][1];
            Z curcoeff1 = aifrom[i][0] * p2inv[aifrom[i][2]];
            tmp += curcoeff1 * (all1 - curtag1[tag]);
            Z curcoeff2 = p2inv[aifrom[i][2]];
            tmp -= curcoeff2 * (all2 - curtag2[tag]);
            all1 += curcoeff2;
            curtag1[tag] += curcoeff2;
            all2 += curcoeff1;
            curtag2[tag] += curcoeff1;
        }
        finalans += tmp;
    }
};

#define DEBUG 0
#define SINGLE 1
#define BT(x, i) (((x) & (1 << (i))) >> (i))
#define fastio std::cin.tie(0) -> sync_with_stdio(0) 

void debug(const char* p){
    #if DEBUG
    freopen(p, "r", stdin); 
    #else
    fastio;
    #endif      
}

void solve(int test){
    int n;
    std::cin >> n;
    p2[0] = 1, p2inv[0] = 1;
    cdt c(n);
    int b[C];
    for(int i = 1, u, v; i < n; ++i){
        std::cin >> u >> v;
        c.addedge(u, v); 
    }
    for(int i = 1; i <= n; ++i){
        std::cin >> a[i];
        b[i] = a[i];
        p2[i] = Z(2) * p2[i-1];
        p2inv[i] = p2[i].inv();
    }
    c.operate(1, -1, nullptr);
    finalans *= p2[n];
    std::cout << finalans.val() << "\n";
}

int main(int argc, char** argv){
    debug(argc==1?"test1.txt":argv[1]);
    int t = 1;
    int test = 1;
    #if !SINGLE
    std::cin >> t;
    #endif
    while(t--){
        solve(test++);
    }
}

Part 1: Problem Statement

Link

A tree $$$T=(V, E)$$$ has $$$n$$$ vertices and $$$n-1$$$ edges, the weight of each vertex $$$i$$$ is $$$a_i$$$.

For each edge $$$e$$$, you can determine its direction, i.e., for two vertices $$$u, v$$$, there are two states: $$$u \rightarrow v$$$ and $$$v \rightarrow u$$$. There are $$$2^{n-1}$$$ states in total.

For each state $$$S$$$, we define $$$f(S)$$$ as

$$$f(S) := \sum\limits_{(u, v) \in V \times V, v\,\text{is reachable from}\,u} |a_u - a_v|$$$.

Compute the sum of $$$f(S)$$$ over all $$$2^{n-1}$$$ states $$$S$$$, modulo $$$998244353$$$.

Example:

Suppose $$$n=3$$$, and two edges connect $$$(1, 2), (2, 3)$$$, respectively. $$$a_1 = 3, a_2 = 1, a_3 = 2$$$, the answer is $$$14$$$.

Constraints: $$$2 \leq n \leq 2 \cdot 10^5$$$, $$$1 \leq a_i \leq 10^9$$$.

Part 2: My idea

My only attempt is using the counting twice trick:

$$$ans = 2\sum\limits_{(u, v) \in V \times V, u < v}|a_u - a_v|2^{n-1-d(u, v)} = \sum\limits_{(u, v) \in V \times V, u < v}|a_u - a_v|2^{n-d(u, v)}$$$, but I don't know how to solve it in $$$O(n)$$$ or $$$O(nlogn)$$$.

Maybe we could use $$$d(u, v) = d(u) + d(v) - 2d(lca(u, v))$$$?

Problem link, link: https://codeforces.com/contest/1679/problem/E

Part 1: Notations

$$$s$$$: The original string that might contain '?'.

$$$s[i,j]$$$: The substring including $$$s[i]$$$ and $$$s[j]$$$: $$$(s[i], s[i+1],..., s[j])$$$. If $$$i > j$$$, the $$$s[i, j]$$$ is an empty string.

$$$t$$$: The query string.

We also define some notations that will be clarified in the Part 2:

$$$ok[i,j]$$$: A $$$2D$$$ bool array indicating whether $$$s[i,j]$$$ is valid or not. We will define the word "valid" in Part 2. If $$$s[i,j]$$$ is valid, then $$$ok[i,j]$$$ is true, i.e., $$$1$$$. If $$$s[i,j]$$$ is invalid, then $$$ok[i,j]$$$ is false, i.e., $$$0$$$.

$$$set[i, j]$$$: The required character set to make $$$s[i,j]$$$ a palindrome.

$$$free[i, j]$$$: The number of free places. We will define the terminology "free places" in part 2.

$$$num[i, j]$$$: The number of '?' in the substring $$$s[i, j]$$$. For example, if s[i, j] == "???a", then $$$num[i, j] == 3$$$.

Part 2: ok, set and free

(1)We call a substring $$$s[i,j]$$$ invalid if and only if:

there exists an index $$$x (i \leq x \leq j)$$$ such that s[x] != '?' && s[i+j-x] != '?' && s[x] != s[i+j-x].

For example,

"ab?a" is valid.

"ax?xc" is invalid because the first character 'a' mismatches with the last character 'c'.

"tbct" is invalid because 'b' != 'c'

The validity of a substring is irrelevant to the query subset. For example, if the query set $$$t$$$ does not contain the character 'b', we still call the string "ab?a" valid, although it certainly cannot form a palindrome. We will deal this case using the $$$set$$$ array.

(2) $$$set[i, j]$$$ denotes all the characters needed to make $$$s[i, j]$$$ a palindrome. For example, if s[i, j] == "ab?a", then set[i, j] == {b}, as we need a character 'b' to fill in the '?'. Note that there are at most $$$17$$$ query characters in this problem, i.e., $$$|t| \leq 17$$$, so we can compress $$$set[i, j]$$$ to a $$$32$$$-bit integer to accelerate computation. Don't use std::set!

(3) $$$free[i, j]$$$ means the number of free characters in the substring $$$s[i, j]$$$. For example, in "ax?xc", the middle '?' is a free character as we could replace it with any character in the query string $$$t$$$. In "ab???a", the first and the second '?' count one free character (Warning: not two!!!). The first '?' can be replaced with an arbitrary character from $$$t$$$, and the second '?' has to be the same with the first '?', so only one of them is free. The third '?' is not free because it has to be 'b'.

Part 3: The naive formula

What is the naive formula for each query string $$$t$$$? It is:

$$$ans(t) = \sum\limits_{1 \leq i,j \leq len(s)} ok[i, j] \cdot [set[i, j] \subseteq t] \cdot |t|^{free[i, j] + num[1, i-1] + num[j+1, len(s)]}$$$ (1)

The $$$[set[i, j] \subseteq t]$$$ is like a Kronecker symbol. If $$$set[i, j] \subseteq t$$$ is true, then $$$[set[i, j] \subseteq t]==1$$$, otherwise $$$[set[i, j] \subseteq t]==0$$$. We need to analyze each $$$i, j$$$. If $$$ok[i, j]$$$ is $$$0$$$, it would never be a palindrome no matter how you fill in the '?'. If $$$ok[i, j]$$$ is $$$1$$$, it depends on the query string $$$t$$$. In part 2, I say that "ab?a" is valid even if $$$t$$$ does not contain 'b'. In this case, $$$ok[i, j]==1$$$ but $$$[set[i, j] \subset t] == 0$$$, the contribution of $$$i,j$$$ is still $$$0$$$. Be careful with the third item, how many strings $$$s$$$ can make $$$s[i, j]$$$ a palindrome? If you only count $$$|t|^{free[i, j]}$$$, you are wrong! Because we can use arbitrary characters to fill in the '?' in $$$s[1, i-1]$$$ and $$$s[j+1, len(s)]$$$, that doesn't affect whether $$$s[i, j]$$$ is a palindrome or not! So, we should not forget $$$num[1, i-1]$$$ and $$$num[j+1, len(s)]$$$.

Part 4: Computation

What is the bottleneck of the naive formula Eq.(1)? Obviously, it takes $$$O(n^2)$$$ for every query, which is too slow. We first figure out:

(1) Computing $$$ok,\,set,\,free$$$ requires $$$O(n^2)$$$ time. Possibly there are $$$O(n)$$$ algorithms, but I don't know. Anyway, $$$O(n^2)$$$ is sufficient to pass. The idea is simple. For odd-length palindromes, we extend from one central character. For even-length palindromes, we extend from two adjacent characters. Initialize the $$$ok$$$ array to $$$0$$$, when you extend, set $$$ok[i, j]$$$ to $$$1$$$, and stop extension when you encounter an invalid pair $$$(i, j)$$$, i.e., s[i] != '?' && s[j] != '?' && s[i] != s[j]. We can compute $$$num$$$ in $$$O(n)$$$ using a prefix array.

(2) After computing $$$ok,\,set\,free$$$ for each $$$(i, j)$$$, try to use these three arrays to precompute $$$ans$$$. We could brute force the length easily in this manner:

for(i, j){ //O(n^2)
   for(int length = 0; length <= 17; ++length){ //O(18)
       ...
   }
}

that is not very difficult. The key problem is when you get a $$$set(i, j)$$$, we should update all its supersets, which might cost $$$O(2^{|t|})$$$ for each $$$(i, j)$$$. We use the "separation of variables trick". We define two $$$dp$$$ arrays, $$$dp1$$$ to solve the original problem and $$$dp2$$$ to solve $$$dp1$$$. The final output is $$$dp2$$$:

$$$dp1[submask][k] := \sum\limits_{1 \leq i,j \leq len(s); set[i, j] == submask; ok[i, j] == 1} k^{free[i, j] + num[1, i-1] + num[j+1, len(s)]}$$$. (2)

$$$dp2[mask][k] := \sum\limits_{submask \subseteq mask} dp1[submask][k]$$$. (3)

$$$ans(t) = dp2[t][|t|]$$$. (4)

This trick is important. You can see that $$$dp2$$$ is irrelevant to the original formula. $$$dp1$$$ could be calculated in $$$O(n^2|t|)$$$ time (we need to brute force the length). You might think the computation of $$$dp2$$$ is hard, but we have a powerful tool for it: The SOSDP! Here is a super good tutorial for SOSDP: https://codeforces.com/blog/entry/45223. If you don't grasp SOSDP, this problem might be hard for you, because SOSDP costs $$$O(2^{|t|}|t|^2)$$$ times to solve it while the naive method costs $$$O(3^{|t|}|t|)$$$! A clarification: The tutorial says SOSDP is $$$O(2^{|t|}|t|)$$$ and the naive method is $$$O(3^{|t|})$$$. This is definitely right. But in this problem, we need to brute force the length, so there is another $$$|t|$$$ in both the SOSDP and the naive methods.

Briefly speaking, SOSDP solves this problem in $$$O(|t|2^{|t|})$$$ time, and this is almost exactly the Eq. (3) in the definition of $$$dp2$$$:

Given $$$G$$$ that maps $$$2^{|t|}$$$ bitmasks to real numbers, calculate $$$F$$$:

$$$F(mask) := \sum\limits_{submask \subseteq mask} G(submask)$$$.

The code is brief:

memcpy(F, G, sizeof(G)); 
for(int i = 0; i < t; ++i) for(int mask = 0; mask < (1<<t); ++mask){ //O(t2^|t|)
	if(mask & (1<<i)) F[mask] += F[mask^(1<<i)];
}

We also note that SOSDP could be used in place, if we don't need the original G after computation. That means the memcpy step could be omitted. The below algorithm is also correct, because when we calculate G[mask], all the submasks of mask are correctly calculated.

//Here: Original G
for(int i = 0; i < t; ++i) for(int mask = 0; mask < (1<<t); ++mask){ //O(t2^|t|)
	if(mask & (1<<i)) G[mask] += G[mask^(1<<i)];
}
//now G is the F and the original G gets lost!

(3)Overall complexity:

$$$O(|t|(n^2 + 2^{|t|}|t| + |q|))$$$. Eq. (2) is $$$O(|t|n^2)$$$, Eq. (3) is $$$O(|t|^22^{|t|})$$$. For each query, we need $$$O(|t|)$$$ times to convert the query string into a $$$32$$$-bit integer. The three parts make the whole complexity.

(4)Submission: here.

According to clist.by, the estimated rating of problem E-Routing is about 2500. I don't think this problem requires a very clever mind, but it contains a lot of evil details that might hinder you from solving it. You might ask me any questions about this problem. Submission is given in the bottom.

Evil detail 1: You should pay attention to the memory limit. Many people tend to put lots of emphasis on time limit but ignore the memory limit. In this problem, the memory limit is a little bit tight. You will get MLE if you use a large array (e.g., int dp[1<<20][20][20]). Key idea: use a bitset. For example, std::bitset or a dynamic bitset. You might use the dynamic bitset in my submission. std::bitset is static because its size is given by the template parameter during the compiling period. In this problem, both static and dynamic bitsets are OK!

Evil detail 2: You should avoid an $$$O(n^3 2^n)$$$ approach. For example, you might define the dynamic programming (dp) as follows: $$$dp[state][x][y]$$$ denotes a Hamilton path starts from $$$x$$$ and ends with $$$y$$$. Then you enumerate all the neighbors $$$z$$$ of $$$y$$$. Be careful, this is $$$O(n^3 2^n)$$$ because you enumerate duplicated circles. To tackle this problem, we still use this $$$dp$$$ array, but we only consider the $$$y, z$$$ that are larger than $$$x$$$. For example, given a Hamilton circuit $$$1-2-3-1$$$, we should enumerate $$$1-2-3-1$$$ only. We should not enumerate $$$2-3-1-2$$$. Each circle is enumerated only once, achieving $$$O(n^2 2^n)$$$ complexity.

Evil detail3: You should be cautious about the sequence of the for loops. Here is a part of my code:

//CORRECT
for(int j = 0; j < (1 << n); ++j){
    for(int start = 0; start < n; ++start){
        for(int end = start; end < n; ++end){
            if(!dp[start][end][j]) continue;
            for(int e2: o[end]){
                if(e2 < start) continue; //Only enumerate the smallest start
                if(BT(j, e2)) continue; //Already enumerated #define BT(x, i) (((x) & (1 << (i))) >> (i))
                int nextj = j|(1<<e2);
                dp[start][e2].set1(nextj);
                pre[nextj][e2] = end;
                if(nb[e2][start]) ok[nextj] = e2;
            }
        }//end of 'end'
    }//end of 'start'
}//end of bitmask 'j'

In the wrong submission, it is:

//WRONG!
for(int start = 0; start < n; ++start){
    for(int end = start; end < n; ++end){
        for(int j = 0; j < (1 << n); ++j){
             ...
        }//end of bitmask 'j'
    }//end of 'end'
}//end of 'start'

Why it is wrong? Because when a bitmask is evaluated, it is not guaranteed that all its subsets are properly handled!

Evil detail 4: You should be careful about the difference between the Hamilton path and the Hamilton circuit. For example, in the below code:

//o[end] is an adjacency list. Every element in this list is adjacent to the vertex end
//nb[a][b] is an adjacency table. nb[a][b]==1 iff a and b are adjacent.
for(int j = 0; j < (1 << n); ++j){
    for(int start = 0; start < n; ++start){
        for(int end = start; end < n; ++end){
            if(!dp[start][end][j]) continue;
            for(int e2: o[end]){
                if(e2 < start) continue; 
                if(BT(j, e2)) continue; 
                int nextj = j|(1<<e2);
                dp[start][e2].set1(nextj); //BECAREFUL: if(nb[e2][start]) dp[start][e2].set1(nextj); is WRONG!
                pre[nextj][e2] = end;
                if(nb[e2][start]) ok[nextj] = e2; //e2 could go back to start, so the vertices in nextj form a Hamilton circuit.
            }
        }//end of 'end'
    }//end of 'start'
}//end of bitmask 'j'

When we execute dp[start][e2].set1(nextj);, should we check whether we can return to start from e2, i.e., there exists an edge connecting start with e2? The answer is NO! Take a simple example: $$$a-b-c-d-a$$$ is a Hamilton circuit, and there isn't an $$$a-c$$$ edge. When we explore $$$c$$$, we should still update the $$$dp[a][c]$$$ item even if there isn't an $$$a-c$$$ edge ($$$a$$$, $$$c$$$ are the start, e2 in the code, respectively). If we don't update the dp table, the algorithm will not explore $$$d$$$!

Evil detail 5: $$$0$$$ or $$$-1$$$, it is a problem. If you are using bitmasks, you might set your arrays $$$0$$$-indexed. So, in these cases, you should be very careful about if(ok), because of some thinking inertias. Sometimes if(ok) should be corrected to if(ok != -1)!

Evil detail 6: You should be careful about the nodes/vertices that are on the Hamilton circuit $$$H$$$. If a vertex $$$v \notin H$$$, we can assign $$$v$$$ to an arbitrary vertex $$$u$$$ that is adjacent to $$$v$$$ from $$$H$$$ . However, if $$$v \in H$$$, we cannot do so. There is an easy counterexample: A Hamilton circuit $$$1-2-3-4-1$$$. If we assign $$$a(1)=2$$$ and $$$a(2)=1$$$, then neither vertex $$$1$$$ nor vertex $$$2$$$ can reach vertex $$$3$$$. They will form a deadlock. So, a construction for $$$v \in H$$$ is $$$a(v) := $$$ the previous vertex of $$$v$$$ on the circuit. For the circuit $$$1-2-3-4-1$$$, we may assign $$$a(1)=4, a(4)=3, a(3)=2, a(2)=1$$$. To achieve this, we need to use another array $$$pre$$$ to record the previous vertex. Its updating is quite similar with the Dijkstra/Floyd algorithm. We might define:

$$$pre[curmask][end]$$$ = the previous vertex of end on the Hamilton circuit curmask.

and do such kinds of update until last==-1:

while(last != -1){ //not fxxking while(last)!
    last = pre[curmask][end];
    curmask ^= (1 << end); //The current end is last, and the current circuit does not contain end, so we should remove it from the curmask.
    end = last;
}

Evil detail 7: I find the problem statements in the Nebius round rather difficult to read. I mean no offense, it is somehow like taking an IELTS reading test. Maybe my English is too poor. I apologize for it. We need to improve our reading efficiency in this round.

Submission (AC, 1356ms).

Problem: https://atcoder.jp/contests/arc156/tasks/arc156_d

My note:

Google drive: https://drive.google.com/file/d/1It475dOHDzrt0DCm0so95x4y7ocn51pT/view?usp=share_link

Tencent: https://docs.qq.com/pdf/DU3pOalBZbW9DbVV1

Code (C/C++ are both OK, please use gcc/g++ compilers), in $$$O(NlogKmax(A))$$$ time:

#include <stdio.h>
#pragma GCC optimize("Ofast") // -Ofast 预编译优化

#define ll long long
ll a[1005];
ll dp[45][2400], pre[45][2400];
ll kbits[45], tot=0;
int main(void){
    //freopen("test1.txt", "r", stdin);
    ll n, k;
    scanf("%lld %lld", &n, &k);
    ll mxa = -1;
    for(ll i = 1; i <= n; ++i){
        scanf("%lld", a+i);
        mxa = a[i] > mxa?a[i]:mxa;
    }
    for(ll bit = 0; bit <= 40; ++bit){ //k一共40位
        if(k & (1ll << bit)){
            ++tot; //tot就是上述分析中的M!
            kbits[tot] = bit;
        }
    }
    dp[0][0] = 1;
    for(ll s = 0; s <= 2*mxa; ++s){
        pre[0][s] = 1;
    }
    for(ll bit = 1; bit <= tot; ++bit){
        for(ll s = 0; s <= 2*mxa; ++s){
            for(ll i = 1; i <= n; ++i){
                if(s >= a[i]){
                    //要注意出界(>2*mxa)的情形
                    ll lb = (s-a[i])<<(kbits[bit]-kbits[bit-1]);
                    ll ub = lb + (1ll<<(kbits[bit]-kbits[bit-1])) - 1ll;
                    if(lb > 2*mxa) continue;
                    if(ub > 2*mxa) ub = 2*mxa;
                    //计算前缀和的时候, 要注意lb==0的情况, 不要搞出0-1==-1这种下标!
                    dp[bit][s] = dp[bit][s] ^ pre[bit-1][ub] ^ (lb?pre[bit-1][lb-1]:0); 
                }
            }
        }
        for(ll s = 0; s <= 2*mxa; ++s){
            pre[bit][s] = (s == 0?dp[bit][s]:(dp[bit][s]^pre[bit][s-1])); //前缀和优化
        }
    }
    ll ans = 0;
    if(n & 1){
        for(ll bit = 1; bit < tot; ++bit){
            for(ll s = 1; s <= 2*mxa; ++s){
                ll curbit = kbits[bit];
                for(ll j = 0; j < kbits[bit+1] - kbits[bit]; ++j){ 
                    //We only care the places between [kbits[bit], kbits[bit+1]). For the places >= kbits[bit+1], dp[bit+1][...] will handle them.
                    //我们只扫描[kbits[bit], kbits[bit+1])之间的位。对于>=kbits[bit+1]的位, 我们让dp[bit+1]帮我们处理。
                    if((s & (1ll << j)) && dp[bit][s]){
                        ans ^= (1ll << (j+curbit));
                    }
                }//for j (bit of s)
            }//for s
        }//for bit
    }
    for(ll s = 1; s <= 2*mxa; ++s){
        ll curbit = kbits[tot];
        for(ll j = 0; j <= 25; ++j){
            if((s & (1ll << j)) && dp[tot][s]){
                ans ^= (1ll << (j+curbit));
            }
        }
    }
    printf("%lld\n", ans);
    return 0;
}