Hello, codeforces.
I think this technique is important, and easy to code, although I haven't found much about it, so I've decided to make a blog explaining it.This technique allows to compare substrings lexicographically in $$$O (1)$$$ with a preprocessing in $$$O (NlogN)$$$.
As this is my first post on codeforces, please let me know if there are any mistakes.
Prerequisites:
- Basic strings knowledge.
- Sparse Table(Optional).
What is a Dictionary of Basic Factors?
As in the sparse table we will have a matrix of size $$$N\log{N}$$$ called $$$DFB$$$, where $$$DFB[i][j]$$$ tells us the position of the string $$$S[i ... i + 2^j-1]$$$ (the first time it appears) among all the strings of size $$$2^j$$$ ordered lexicographically.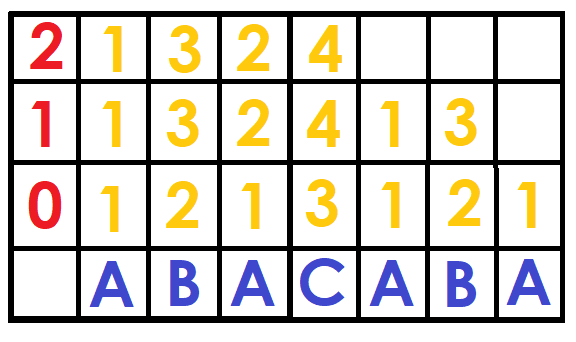
So, how do we build the matrix? Let's start with the lowest level, for powers of size $$$2^0$$$, we simply put the position of the character $$$S[i]$$$ in the dictionary (1 for 'A', 2 for 'B' ... and so on).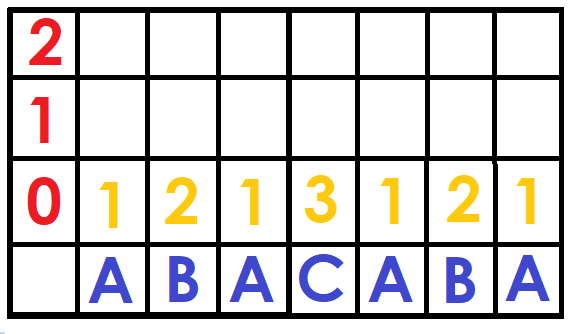
For the following $$$ DFB[i][j] $$$ we can save a pair of numbers that are $$$(DFB[i][j-1], DFB[i+2^{j-1}][j-1]) $$$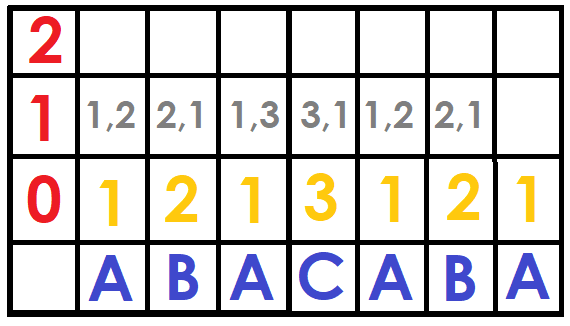
Now we replace the pairs by their position (the first time the pair appears) on the ordered array of those pairs. This can be done with Radix Sort in $$$O(N)$$$, otherwise with a normal sort in $$$O(NlogN)$$$ (But this will slow down the algorithm).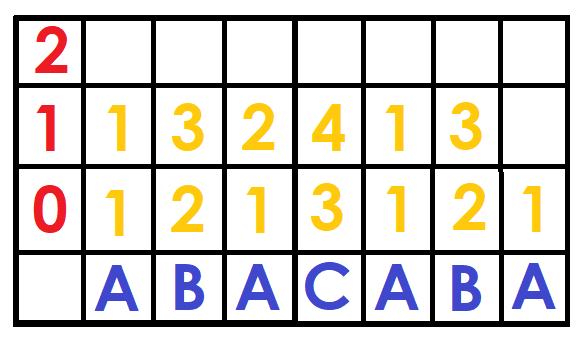
We do that for all powers of two and we will have the complete matrix.
Handling queries:
Suppose we want to make a query that is "Say which of the two substrings $$$S[l_{1}...r_{1}]$$$ and $$$S[l_{2}...r_{2}]$$$ is smaller lexicographically?".
First of all, let's analyze that if the substrings have different sizes, we can compare only the prefixes of size $$$M$$$ where $$$M$$$ is the minimum size between the two substrings, if both prefixes are equal then the smallest lexicographically is the substring of smaller size.
As in the Sparse Table, suppose $$$ k = \ log {(r-l)} $$$, then we can represent the substring $$$ S [l ... r] $$$ as the pair $$$ ( DBF [l] [k], DFB [r-2^k+1] [k] ) $$$. Now to compare two substrings of equal size we simply lexicographically compare their pairs in $$$O(1)$$$.
For example, suppose we have the string "ABACABA" and we want to know which string is lexicographically smaller between $$$ S [0 ... 5] $$$ and $$$ S [1 ... 6] $$$ ("ABACAB" and "BACABA").Since $$$\log{(5-0)}=2$$$, the pairs to compare would be: $$$(DBF [0] [2], DBF [2] [2])$$$ and $$$(DBF [1] [2], DBF [3] [2])$$$, which would be $$$(1,2)$$$ and $$$(2,4)$$$ therefore the first substring is lexicographically smaller. 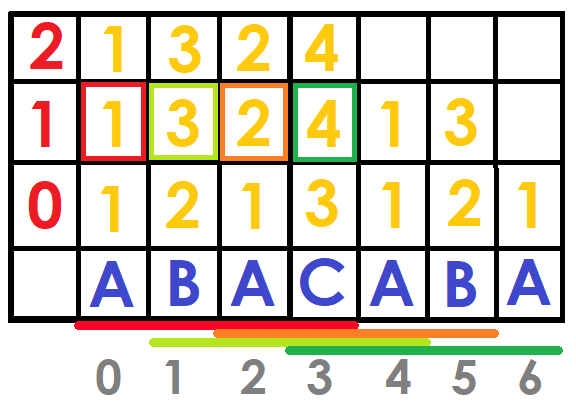
Proof:
Since we have that $$$DBF [i] [j]$$$ is the position of $$$ S [i ... i + 2 ^ j + 1] $$$ between all substrings of size $$$ 2 ^ j $$$. If we want to compare two substrings, which would be represented as pairs, and we compare the first element in the pairs, we are comparing prefixes of size $$$ 2 ^ k $$$ of the substrings (where $$$k$$$ is the logarithm of the size of the substring). If they are the same, we compare the second elements of the pairs, which would be the same as comparing suffixes of size $$$ 2 ^ k $$$ of the substrings.
This technique can also be used to build the suffix array (If you still don't know how to do it, check this link, you have already learned most of it).
Implementation in a suffix array made by Tet .
Thanks for reading, I hope this article will be useful. Any questions or suggestions let me know in the comments.










