Hi, I was trying to solve this standard problem on complement graph traversal. Following are 2 almost similar solutions where one TLE's and the other passes, I'm not able to see where is the inefficiency coming in for the TLE solution, is it the complexity or just poor implementation.
TLE SOLUTION
AC SOLUTION
I understand the complexity of the second solution is $$$\mathcal{O}((N+M)\log N)$$$ as the number of times we check if an edge is present or not is $$$\mathcal{O}(M)$$$, but I'd be grateful if someone can outline the issue/complexity with/of the TLE solution.
| # | User | Rating |
|---|---|---|
| 1 | ecnerwala | 3649 |
| 2 | Benq | 3581 |
| 3 | orzdevinwang | 3570 |
| 4 | Geothermal | 3569 |
| 4 | cnnfls_csy | 3569 |
| 6 | tourist | 3565 |
| 7 | maroonrk | 3531 |
| 8 | Radewoosh | 3521 |
| 9 | Um_nik | 3482 |
| 10 | jiangly | 3468 |
| # | User | Contrib. |
|---|---|---|
| 1 | maomao90 | 174 |
| 2 | awoo | 164 |
| 3 | adamant | 161 |
| 4 | TheScrasse | 159 |
| 5 | nor | 158 |
| 6 | maroonrk | 156 |
| 7 | -is-this-fft- | 152 |
| 8 | SecondThread | 147 |
| 9 | orz | 146 |
| 10 | pajenegod | 145 |
Almost every day a blog by This user pops up in recent actions. These blogs just have 1000 lines cursing codeforces or mike, and since these blogs are too long, not everyone cares to scroll down till the bottom to downvote it. I request the moderators to please ban this guy. (We can always ignore it but I thought it unnecessarily clutters recent actions and other topics which actually deserve attention might get neglected.)
Hi, I was trying to solve this problem from CSES problemset and I myself wasn't able to solve it but I checked a few submissions and noticed the following as the simplest approach to solve this problem.
ALGORITHM:
We create a new array $$$D$$$ where $$$D_i=A_i-B_i$$$(the excess or deficit for that particular element) and we create a prefix array $$$\displaystyle P_i=\sum_{j=1}^iD_i$$$ and then sort it. Once sorted we do the usual median trick where we sum up the absolute differences with the median for each element $$$P_i$$$ and report that sum as the answer.
Now I have the following explanation of why this algorithm works.
Once we create prefix array $$$P$$$ from $$$D$$$ difference between any 2 elements $$$P_i-P_{j-1}$$$ gives the total deficit/extra in the subarray $$$D[i \dots j]$$$ and since we want to achieve a state where $$$D_i=0 \ \forall 1 \le i \le N $$$ hence we want $$$P_i-P_j=0$$$ for any i and j. hence we try to bring all $$$P_i$$$'s to a single value using a minimum number of moves and that's a very standard problem where we bring everything to the median.
Can anyone confirm if my inference is correct or not?
Now here I have 3 questions:
1.When we make some non-median $$$P_i$$$ equal to the median by doing $$$\displaystyle|P_i-P_{\frac{N}{2}}|$$$ operations won't the other prefix values change for all $$$j$$$ where $$$i \le j \le N$$$ since all such $$$P_j$$$'s are dependent on $$$P_i$$$, so what makes us ignore that fact?
2.Here we're given that the array is circular so where is this fact coming into play?
3.How will we solve the problem if array had not been circular?
My apologies if I asked something very lame, I'd grateful if anyone can help me with this :)
Hello friends, I was trying to solve this dynamic programming problem. The editorial proposes an $$$\mathcal{O}(N^4)$$$ solution to this problem, but I think it could be solved in $$$\mathcal{O}(N^3)$$$ time according to the following approach:
Say, $$$i \le e_k \le j \rightarrow$$$ kth occurence of $$$A[i]$$$ between $$$i$$$ and $$$j$$$, $$$K \rightarrow$$$ number of occurrences of $$$A[i]$$$ in $$$[i\dots j]$$$ . Transitions are as follows.
Unfortunately, this approach gives WA. I'd be grateful if anyone could share an $$$\mathcal{O}(N^3)$$$ or an intuitively more convincing $$$\mathcal{O}(N^4)$$$ solution as I was not able to follow the editorial completely.
Hi, can anyone tell if there's a way to stress test solution to an interactive problem by running it over hundreds of test cases ?
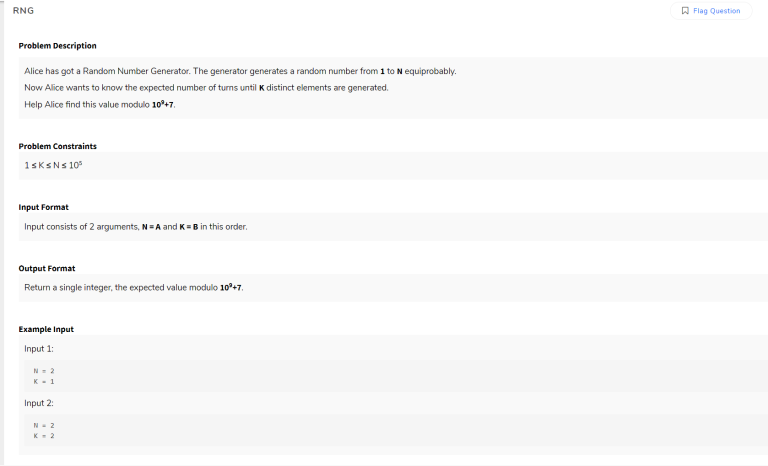
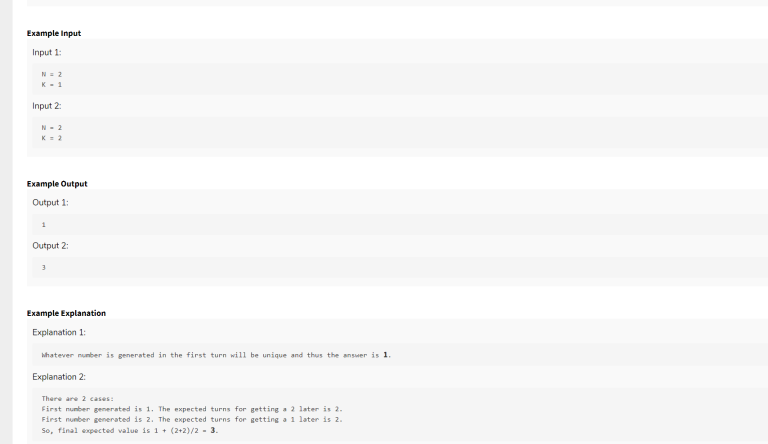
Hi, I was trying to solve this problem which I got in a Codenation Coding Test, unfortunately I don't have the link for the problem. I've been trying this problem for a while but couldn't come up with a working approach. It'd be great if someone can share their ideas to solve this problem. The test is over 4 months back so be assured that it's not from an on going contest.
Hi, I was trying to solve this problem. And after going through a couple of submissions (Here is a neat one) I got the transition recurrence but I am still not able to work around the intuition behind it. Can someone please explain a little about what are the pointers which lead you this recurrence and also I am sorry if it's a standard dp type(if possible please share some resource or problem based on the same idea :P)
With his fiery 25th place in Codeforces Round #683 SecondThread became International Gradmaster. My Heartiest Congratulations to him. Also I thank him for his invaluable contribution to the community. #SecondThread orz
Hi, I was trying to solve this problem from a coding test and came up with an O(n^4) solution which goes like first I will precompute the 2-D prefix sums of the entire grid and then for each cell naively Bruteforce for all possible solutions in n^2 operations, It would be great if you can share your insights/solutions for the problem. The contest is over 5 days back you can answer as late as you want until you are assured of this.

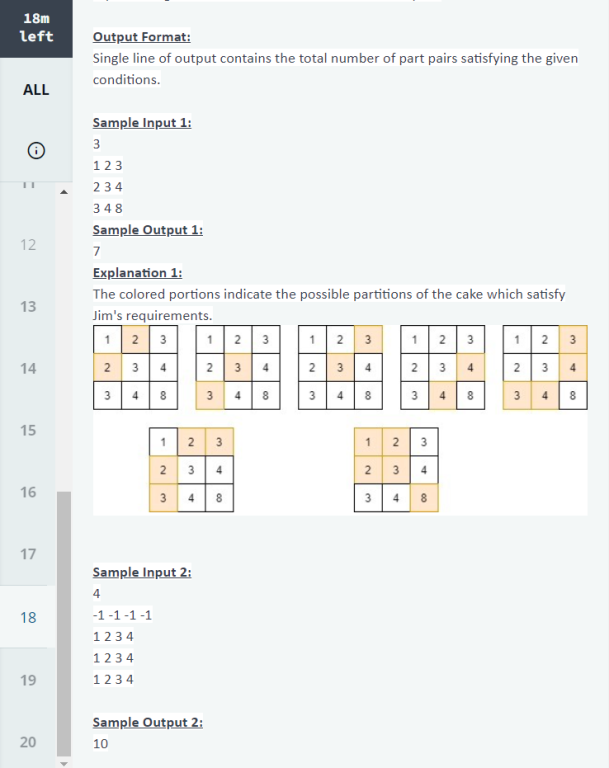
| Name |
|---|










