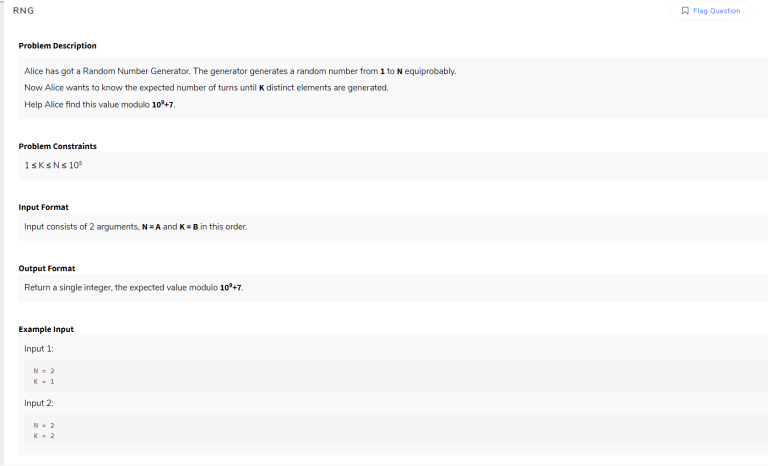
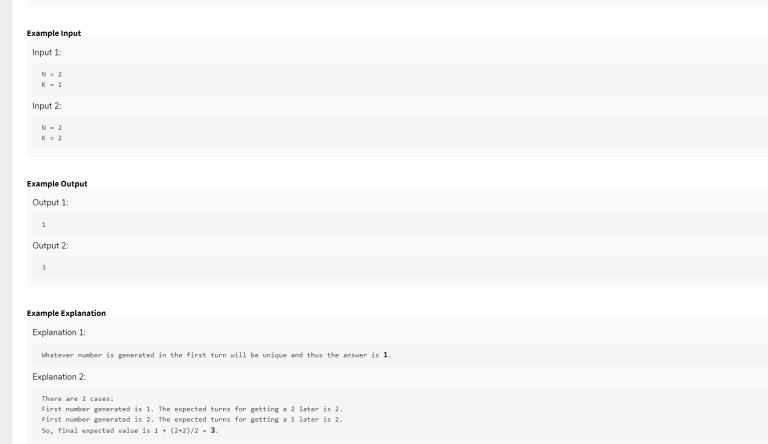
PROBLEM_STATEMENT
Hi, I was trying to solve this problem which I got in a Codenation Coding Test, unfortunately I don't have the link for the problem. I've been trying this problem for a while but couldn't come up with a working approach. It'd be great if someone can share their ideas to solve this problem. The test is over 4 months back so be assured that it's not from an on going contest.










I might be wrong, but I think the answer is $$$\frac{N}{N}+\frac{N}{N-1}+\cdots+\frac{N}{N-K+1}$$$. Before you get $$$K+1$$$ distinct numbers, you need to get $$$K$$$ distinct numbers. From there, you have an $$$\frac{N-K}{N}$$$ probability of picking a new number and reaching $$$K+1$$$, so $$$E(K+1) = E(K) + \frac{1}{(\frac{N-K}{N})}$$$ and we arrive at the consequential formula.