Continuing with the theme of absent editorials for old rounds, here is an editorial for Codeforces Round 171 (Div. 2). Even though there is an official editorial, it is only in russian and doesn't have solution for the last problem.
A
279A - Point on Spiral
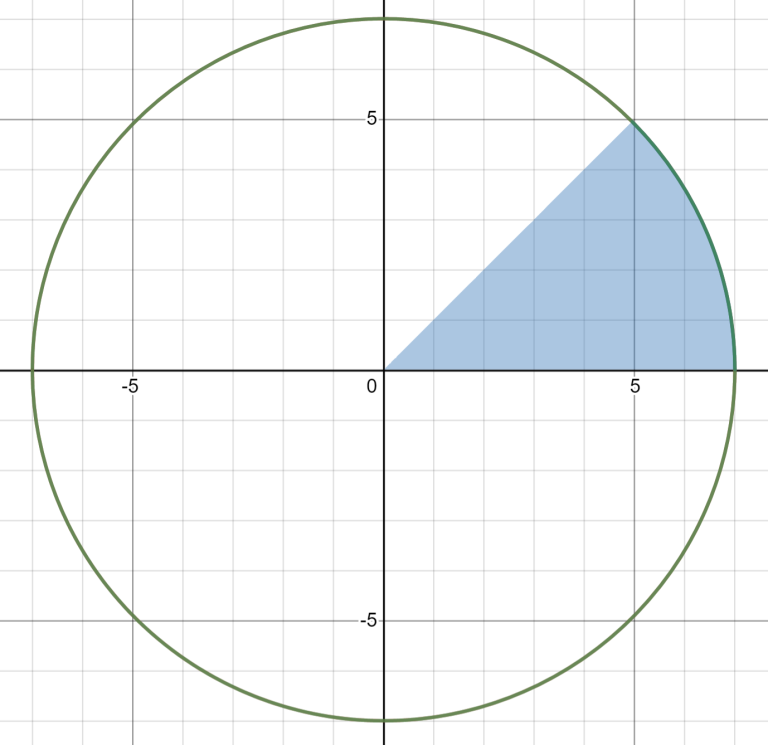
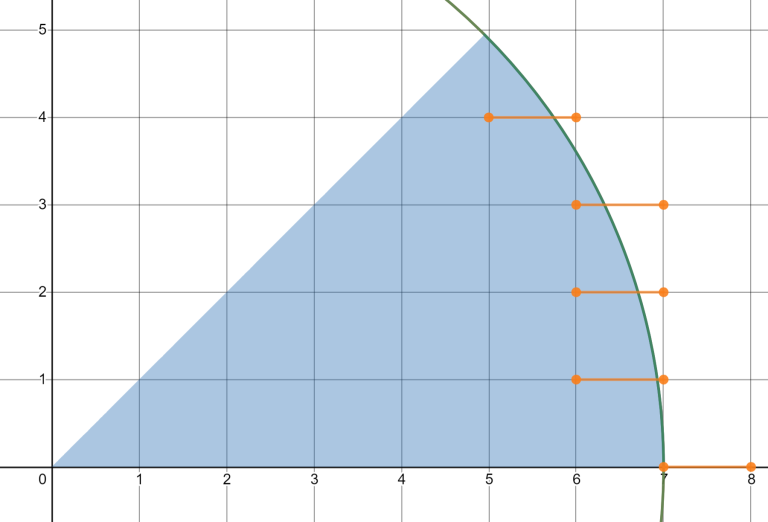
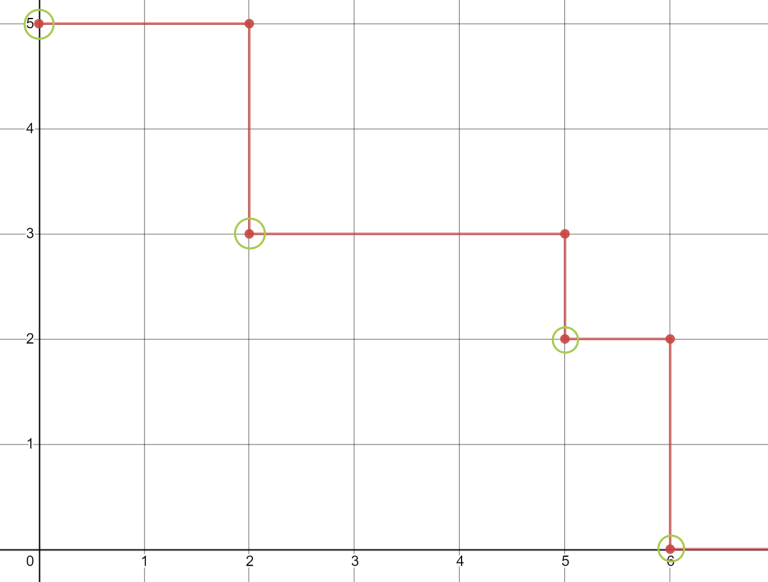
Since constraints are small, you can just simulate the whole process, but I'll explain an $$$O(1)$$$ solution. Let's look at the path
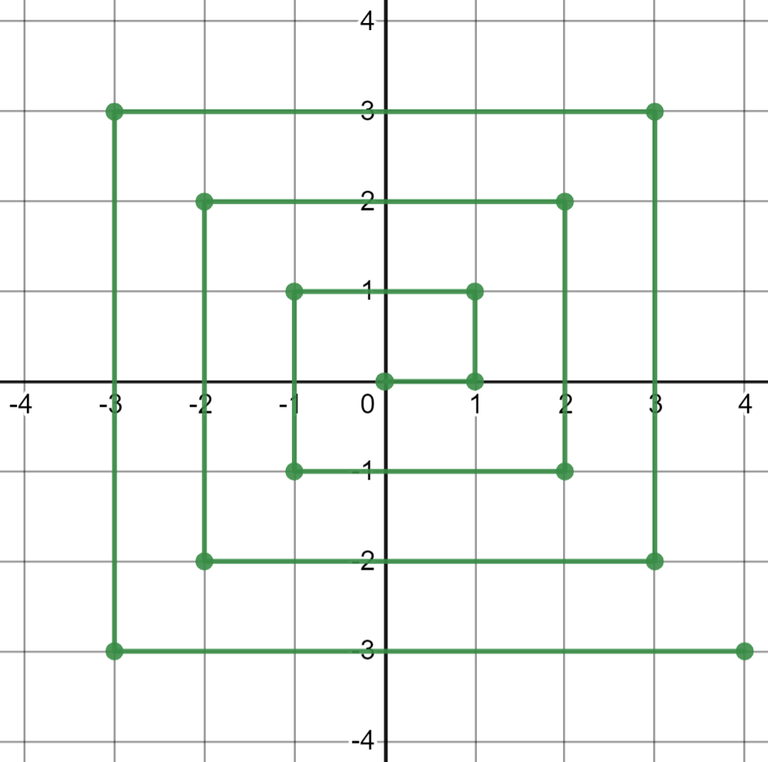
Now it's easy to see that the plane can be divided into four parts
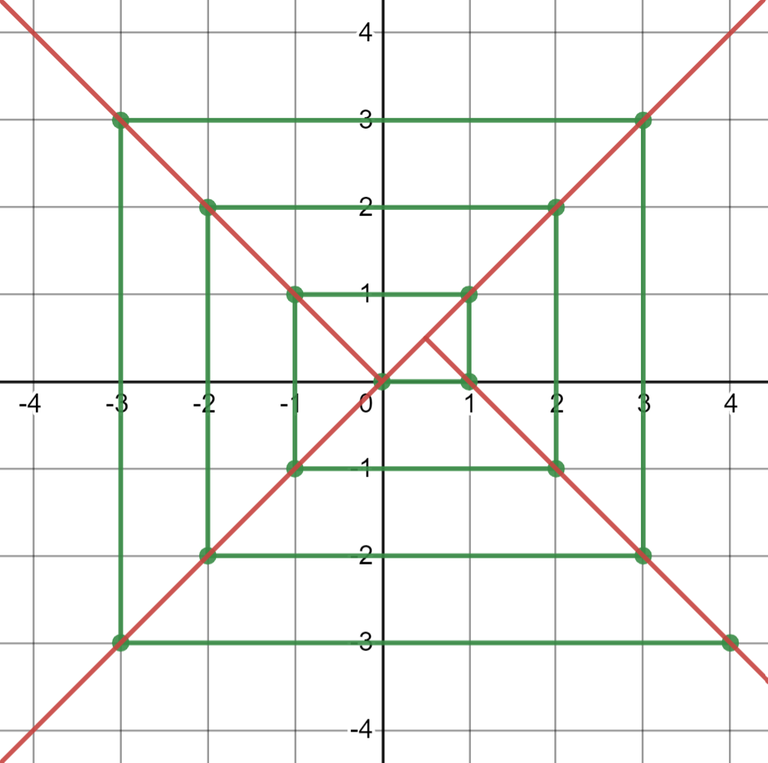
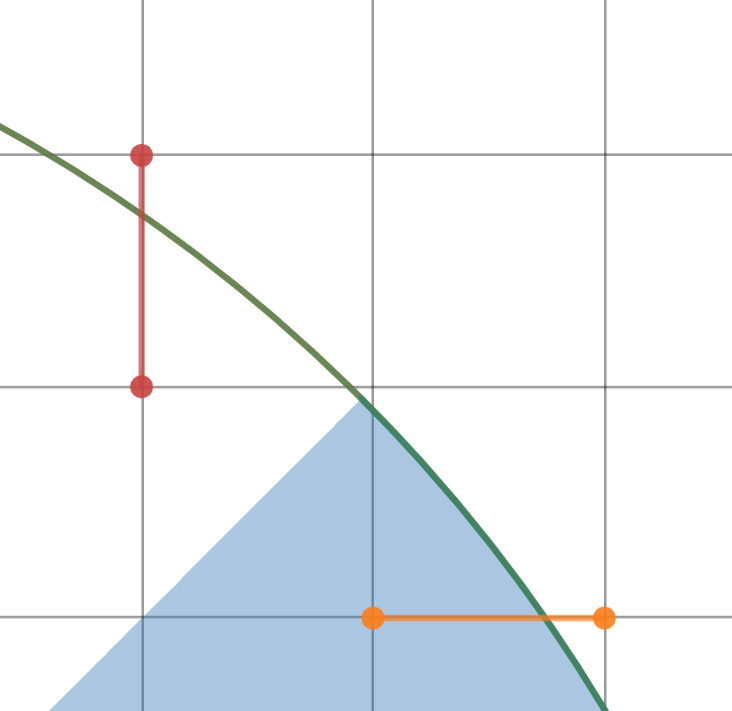
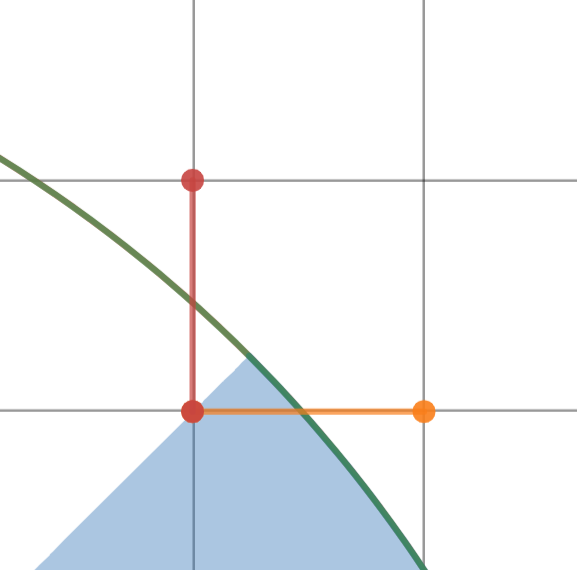
And then we can calculate answer for each part separately, just be careful with borders. For example, for the right part the answer is $$$4x - 3$$$.
#include "bits/stdc++.h"
using namespace std;
int main() {
int x, y;
cin >> x >> y;
if (x == 0 && y == 0) {
cout << 0 << '\n';
} else if (-x + 1 < y && y <= x) {
cout << 1 + (x - 1) * 4 << '\n';
} else if (-y <= x && x < y) {
cout << 2 + (y - 1) * 4 << '\n';
} else if (x <= y && y < -x) {
cout << 3 + (-x - 1) * 4 << '\n';
} else {
cout << 4 + (-y - 1) * 4 << '\n';
}
return 0;
}
B
279B - Books
The problem can be written in the following way: for each index $$$i$$$ denote $$$r_i$$$ as the largest index such that $$$a_i + \ldots + a_{r_i} \leqslant t$$$. The problem is to find $$$max(r_i - i + 1)$$$.
One can see that $$$r_i$$$ are nondecreasing, so the problem can be solved with two pointers: iterate over $$$i$$$ and keep a pointer to corresponding $$$r_i$$$.
#include "bits/stdc++.h"
using namespace std;
int main() {
int n, t;
cin >> n >> t;
vector<int> a(n);
for (int& k : a)
cin >> k;
int r = 0;
int sm = 0;
int ans = 0;
for (int i = 0; i < n; ++i) {
while (r < n && sm + a[r] <= t) {
sm += a[r];
++r;
}
ans = max(ans, r - i);
sm -= a[i];
}
cout << ans << '\n';
return 0;
}
C
279C - Ladder
Let's calculate two arrays before answering queries. $$$tol[i]$$$ is the smallest index such that $$$[b_{tol[i]},\, \ldots,\, b_{i}]$$$ is nonincreasing, and $$$tor[i]$$$ is the largest index such that $$$[b_{i},\, \ldots,\, b_{tor[i]}]$$$ is nondecreasing. Then for each query we can take $$$tor[l]$$$ and $$$tol[r]$$$ and compare them. The answer is "Yes" iff $$$tor[l] \geqslant tol[r]$$$. In other words, we are checking if the largest nondecreasing segment from $$$l$$$ and largest nonincreasing segment from $$$r$$$ are intersecting.
To calculate $$$tol[i]$$$, go over $$$i$$$ from $$$1$$$ to $$$n$$$ and maintain largest nonincreasing suffix. For $$$tor$$$ do the same in reverse.
#include "bits/stdc++.h"
using namespace std;
int main() {
int n, m;
cin >> n >> m;
vector<int> a(n);
for (int& k : a)
cin >> k;
vector<int> tor(n), tol(n);
iota(tol.begin(), tol.end(), 0);
iota(tor.begin(), tor.end(), 0);
tol[0] = 0;
for (int i = 1; i < n; ++i)
if (a[i - 1] >= a[i])
tol[i] = tol[i - 1];
tor[n - 1] = n - 1;
for (int i = n - 2; i >= 0; --i)
if (a[i] <= a[i + 1])
tor[i] = tor[i + 1];
while (m--) {
int l, r;
cin >> l >> r;
--l; --r;
cout << (tol[r] <= tor[l] ? "Yes" : "No") << '\n';
}
return 0;
}
D
279D - The Minimum Number of Variables
You can notice that when we want to perform some operation, we are only interested in a subset of current values of variables (including zeros). So let's create $$$dp[i][mask] = bool$$$, which is $$$1$$$ if we can perform first $$$i$$$ operations and end up with the values from $$$mask$$$. Here $$$k$$$-bit in the mask corresponds to the value $$$vals[k]$$$, where array $$$vals$$$ stores all numbers in $$$a$$$ and a zero, and $$$k$$$-th bit is set iff the value of one of the variables is $$$vals[k]$$$.
To make transition from $$$dp[i][mask]$$$ to $$$dp[i + 1][new\_mask]$$$, let's look at the operation. We have to find two values in the $$$mask$$$ such that their sum is $$$a[i + 1]$$$. Then to calculate $$$new\_mask$$$ we have to set $$$k$$$-th bit in the $$$mask$$$, where $$$k$$$ is such that $$$vals[k] = a[i + 1]$$$. Also, while writing new variable we can overwrite any existing variable, so we have an option to disable any bit in the $$$mask$$$.
Now it looks like we have $$$O(2^nn)$$$ states and $$$n$$$ transitions from each state (disabling each bit). But actually if we only make transition from $$$dp[i][mask] = 1$$$, the complexity will be $$$O(2^nn)$$$, because for each $$$i$$$ there are at most $$$2^{i+1}$$$ masks that we can achieve, since there are only $$$i$$$ distinct numbers on the current prefix plus an additional zero. And $$$\sum_{i=1}^n 2^{i+1}\cdot n = O(2^nn)$$$.
The only problem left is to check if we can build some number $$$y$$$ from $$$vals$$$ using numbers from $$$mask$$$. This can be precomputed in $$$O(2^nn)$$$: let's calculate array $$$possible[mask] = x$$$, where $$$i$$$-th bit in $$$x$$$ is set iff we can get number $$$vals[i]$$$ from mask on the next step. To calculate it, first for each $$$mask$$$ with at most $$$2$$$ bits just calculate all possible $$$x$$$ with any straightforward approach, since there are only $$$O(n^2)$$$ such masks. For any other mask notice that we can get $$$y$$$ iff sum of some two values equals to $$$y$$$. So we can iterate over all submasks such that they differ from $$$mask$$$ in exactly one bit and update $$$possible[mask]$$$ with $$$possible[submask]$$$. And since $$$mask$$$ has at least $$$3$$$ bits, if there is a pair which sums up to $$$y$$$, this pair will be included into at least one of the submasks. One can even notice that we only need any $$$3$$$ such submasks to cover every pair of bits.
The answer is minimum number of bits over all masks such that $$$dp[n][mask] = 1$$$.
#include "bits/stdc++.h"
using namespace std;
int main() {
int n;
cin >> n;
vector<int> a(n);
for (int& k : a)
cin >> k;
auto vals = a;
vals.push_back(0);
sort(vals.begin(), vals.end());
vals.erase(unique(vals.begin(), vals.end()), vals.end());
vector<int> pos(n);
for (int i = 0; i < n; ++i) {
pos[i] = lower_bound(vals.begin(), vals.end(), a[i]) - vals.begin();
}
vector<int> possible(1 << vals.size(), 0);
for (int i = 1; i < possible.size(); ++i) {
int k = 0;
for (int j = 0; j < vals.size() && k < 3; ++j) {
if ((i >> j) & 1) {
possible[i] |= possible[i ^ (1 << j)];
++k;
}
}
if (__builtin_popcount(i) <= 2) {
for (int j = 0; j < vals.size(); ++j) {
if (!((i >> j) & 1)) continue;
for (int k = 0; k < vals.size(); ++k) {
if (!((i >> k) & 1)) continue;
int val = vals[j] + vals[k];
int ind = lower_bound(vals.begin(), vals.end(), val) - vals.begin();
if (ind < vals.size() && vals[ind] == val)
possible[i] |= (1 << ind);
}
}
}
}
vector<char> dp_cur(1 << vals.size(), 0);
dp_cur[1 << pos[0]] = 1;
dp_cur[(1 << pos[0]) | (1 << 0)] = 1;
auto can_sum = [&](int mask, int pos) {
return (possible[mask] >> pos) & 1;
};
vector<char> dp_next;
for (int i = 1; i < n; ++i) {
dp_next.assign(dp_cur.size(), false);
for (int j = 0; j < dp_cur.size(); ++j) {
if (dp_cur[j] && can_sum(j, pos[i])) {
int mask = j;
mask |= (1 << pos[i]);
dp_next[mask] = 1;
for (int k = 0; k < vals.size(); ++k)
if (((mask >> k) & 1) && vals[k] != a[i])
dp_next[mask ^ (1 << k)] = 1;
}
}
swap(dp_cur, dp_next);
}
int ans = -1;
for (int i = 0; i < dp_cur.size(); ++i) {
if (!dp_cur[i]) continue;
int sz = __builtin_popcount(i);
if (ans == -1 || ans > sz)
ans = sz;
}
cout << ans << '\n';
return 0;
}
E
279E - Beautiful Decomposition
First of all it's easy to notice that we will use each power of $$$2$$$ at most once.
Let's look at the highest bit in the current number, suppose it's $$$2^k$$$. Since the sum of all powers of $$$2$$$ below $$$k$$$ is less than $$$2^k$$$, we will have to add at least one power of two $$$2^x$$$ with $$$x \geqslant k$$$. One can see that adding $$$2^{k+2}$$$ is not optimal, since then we will have to subtract at least $$$2^{k+1}$$$ and $$$2^{k+2} - 2^{k+1}$$$ can be replaced with $$$2^{k+1}$$$. So the only choices are $$$2^k$$$ or $$$2^{k+1}$$$. If we add $$$2^k$$$, we have to solve a problem for remaining number, which is a suffix or our current binary string. Otherwise, $$$2^{k+1}$$$ is larger than our current number, so we just need the answer for $$$m = 2^{k+1} - n$$$. Let's call such $$$m$$$ a complement for a number $$$n$$$ (notice that we don't need $$$k$$$ in the definition because $$$k$$$ is defined as largest bit in $$$n$$$)
Now let's look at $$$m$$$. To calculate it, we have to flip all bits in $$$n$$$ and add $$$1$$$ to the result. Now it's easy to see that if $$$m$$$ is a complement for $$$n$$$, then for any suffix of $$$n$$$ (in binary form), the corresponding suffix of $$$m$$$ is a complement for it. Also, $$$n$$$ is a complement for $$$m$$$.
So during our calculations we will only deal with $$$n$$$, $$$m$$$, suffixes of $$$n$$$ and suffixes of $$$m$$$. And this leads to a following dp solution: let $$$v[1] = n$$$, $$$v[2] = m$$$. Then $$$dp[ind][suf]$$$ is the smallest answer for a binary number represented by a suffix of number $$$v[ind]$$$ starting from index $$$suf$$$. We can calculate this $$$dp$$$ starting from $$$dp[\ldots][n]$$$ and the answer will be $$$dp[1][1]$$$.
#include "bits/stdc++.h"
using namespace std;
int main() {
string n;
cin >> n;
string m = n;
{
for (char& c : m) {
c ^= '1' ^ '0';
}
int ind = m.size() - 1;
while (ind >= 0 && m[ind] == '1') {
m[ind] = '0';
--ind;
}
if (ind == -1) {
m.insert(m.begin(), '1');
n.insert(n.begin(), '0');
} else {
m[ind] = '1';
}
}
int sz = n.size();
vector<string> v = {n, m};
vector<array<int, 2>> dp(sz);
dp[sz - 1][0] = (v[0].back() == '1');
dp[sz - 1][1] = (v[1].back() == '1');
for (int i = sz - 2; i >= 0; --i) {
for (int b = 0; b < 2; ++b) {
if (v[b][i] == '0') {
dp[i][b] = dp[i + 1][b];
} else {
dp[i][b] = min(dp[i + 1][b] + 1, dp[i + 1][b ^ 1] + 1);
}
}
}
cout << dp[0][0] << '\n';
return 0;
}