I was recently puzzled by this problem:
- Given $$$n$$$ intervals $$$[l_i,r_i]$$$. Find the lexicographically minimum permutation $$$p_1,p_2,\dots,p_n$$$ of $$$1-n$$$ such that $$$p_i\in [l_i,r_i]$$$ for each $$$1\leq i\leq n$$$.
This problem comes from misreading the problem A Place For My Head from Petrozavodsk Summer 2017. Day 5. Moscow IPT Contest. The original problem requires that $$$q_i\in [l_i,r_i]$$$ where $$$q=p^{-1}$$$ is the inverse permutation of $$$p$$$ and has constraint $$$1\leq n\leq 2\times 10^5$$$.
I wonder if there exists a decent (subquadratic) solution for this (misread version) of the problem? Many thanks in advance!








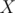 and three subsets
and three subsets 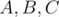 , To obtain
, To obtain 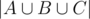 , we take the sum
, we take the sum 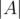 +
+ 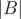 +
+ 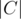 . Unless
. Unless  has been counted twice. So we subtract
has been counted twice. So we subtract  . Now the count is correct except for the elements in
. Now the count is correct except for the elements in 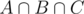 which have been added three times, but also subtracted three times. The answer is therefore
which have been added three times, but also subtracted three times. The answer is therefore 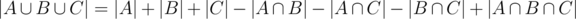
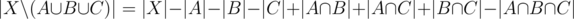
 be subsets of
be subsets of 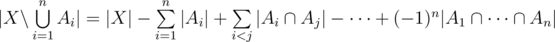
 is counted in both sides. If
is counted in both sides. If 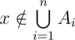 , then it's counted once on either side. Suppose
, then it's counted once on either side. Suppose 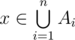 , and more precisely, that
, and more precisely, that  is in exactly
is in exactly  of the sets
of the sets  . The count on the left-hand side is
. The count on the left-hand side is  , and on the right hand side, we have
, and on the right hand side, we have 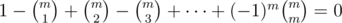
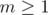 , thus the equality holds.
, thus the equality holds.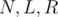 , you need to compute the number of integers
, you need to compute the number of integers 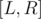 such that
such that 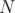 , that is,
, that is, 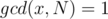 . There are
. There are 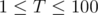 testcases. Constraints:
testcases. Constraints: 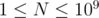 ,
, 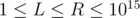 .
. 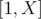 such that
such that 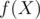 , then the answer is
, then the answer is 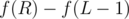 . How we're gonna compute
. How we're gonna compute 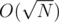 and then find all prime factors
and then find all prime factors 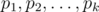 of
of 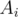 be the set of numbers that are divisible by
be the set of numbers that are divisible by 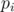 , then the answer is the
, then the answer is the 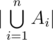 , which may be hard to compute directly. However, using the restricted inclusion-exclusion principle, we can convert the problem into computing the size of the intersection of sets, which is trivial. Time complexity is
, which may be hard to compute directly. However, using the restricted inclusion-exclusion principle, we can convert the problem into computing the size of the intersection of sets, which is trivial. Time complexity is 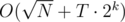 , with
, with 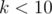 equals to the number of distinct prime factors of
equals to the number of distinct prime factors of 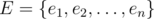 of properties that the elements of
of properties that the elements of 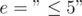 ,
, 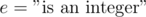 , or even
, or even 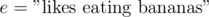 . Let
. Let 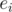 (and possibly others). Then
(and possibly others). Then 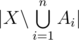 is the number of elements that process none of the properties. Clearly,
is the number of elements that process none of the properties. Clearly, 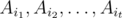 is the set of elements that possess the properties
is the set of elements that possess the properties 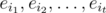 (and maybe others). Using the notation
(and maybe others). Using the notation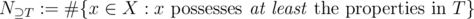
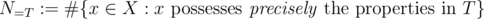
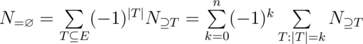
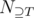 depends only on the size
depends only on the size 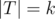 . We can then write
. We can then write 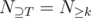 for
for 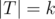 , and call
, and call 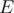 a homogeneous set of properties, and in this case
a homogeneous set of properties, and in this case 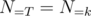 also depends only on the cardinality of
also depends only on the cardinality of 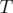 . Hence for homogeneous properties, we have
. Hence for homogeneous properties, we have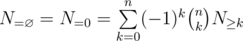
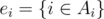 , we arrive at the restricted inclusion-exclusion principle.
, we arrive at the restricted inclusion-exclusion principle. , satisfying that
, satisfying that 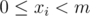 , modulo
, modulo 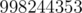 . Constraints:
. Constraints: 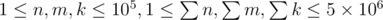 . Hint: the number of non-negative integer solutions to
. Hint: the number of non-negative integer solutions to  is given by
is given by  .
.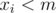 . To do that, we apply the inclusion-exclusion principle. Let
. To do that, we apply the inclusion-exclusion principle. Let 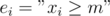 , then
, then 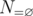 is our desired answer. Clearly, this set of properties is homogeneous. Take
is our desired answer. Clearly, this set of properties is homogeneous. Take  , then
, then 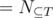 is the number of solutions with
is the number of solutions with 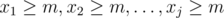 . Setting
. Setting 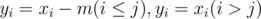 , and it's the same as the number of solutions of the system
, and it's the same as the number of solutions of the system 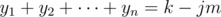
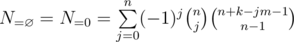
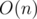 , due to precomputing factorials and the modular inverses of factorials.
, due to precomputing factorials and the modular inverses of factorials. . Constraint:
. Constraint: 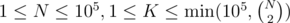 .
.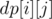 as the number of permutations of length
as the number of permutations of length  with
with 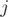 inversions. The recurrence is also trivial:
inversions. The recurrence is also trivial: 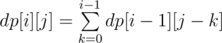 . This is
. This is 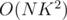 , and can be optimized to
, and can be optimized to 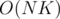 using prefix sums, which is still not enough due to the given constraints.
using prefix sums, which is still not enough due to the given constraints. to the number of inversions, so the answer is equal to the number of solutions to
to the number of inversions, so the answer is equal to the number of solutions to  .
.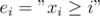 , then
, then  , then the number of solutions to the equation is
, then the number of solutions to the equation is 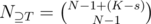 . Therefore, we can group those sets together. By inclusion-exclusion principle,
. Therefore, we can group those sets together. By inclusion-exclusion principle, 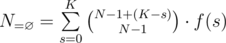
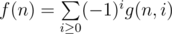
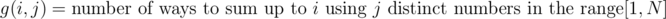 .
.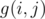 . We can use the technique as we can computing partition numbers. Partition
. We can use the technique as we can computing partition numbers. Partition  in the set or not, and then we get the recurrence
in the set or not, and then we get the recurrence 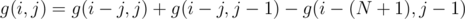 . Another important observation is that there are at most
. Another important observation is that there are at most 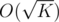 valid values for
valid values for 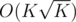 .
.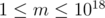 .
.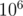 , and then what remains, is a prime
, and then what remains, is a prime 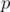 , a square of a prime
, a square of a prime 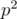 , or a product of two distinct primes
, or a product of two distinct primes 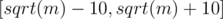 to check if it's the second case, and otherwise the last case.
to check if it's the second case, and otherwise the last case.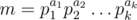 . We need to avoid counting the cases with
. We need to avoid counting the cases with 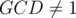 and
and 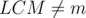 , thus we should apply inclusion-exclusion principle. Let
, thus we should apply inclusion-exclusion principle. Let 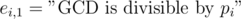 and
and 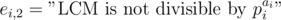 . Then the answer is
. Then the answer is 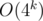 ,which is too much for
,which is too much for 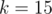 in te worst case. However, noticing that two of the options of for each prime divisor lead to same computations, the complexity can be reduced to
in te worst case. However, noticing that two of the options of for each prime divisor lead to same computations, the complexity can be reduced to 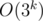 .
.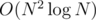 using FFT. Furthermore, since we only concern the answer with
using FFT. Furthermore, since we only concern the answer with 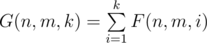 modulo
modulo 
