This is a problem in CSAcademy Contest Romanian IOI 2017 Selection #3, Pitmutation, which basically is: Given two permutations A, B of length N with some positions fixed while some positions remains unknown, find the number of configurations such that there are exactly S positions p1, p2, ..., pS, where Api > Bpi, both N, S ≤ 300.
I've already come up a solution when there are no fixed positions. For simplicity, we can consider B as identity permutation and later multiply the answer by N!. Then we decompose the permutation into cycles. Let dp[i][j] denote the number of configurations, when there are i elements remaining, and the needed number of Api > Bpi positions is j. Enumerate the length of cycle the smallest element is in for transferring, which involves precalculating another DP: dp2[i][j] denote the number of permutations A of length i that consists of one cycle such that there are j positions x where Ax > A(x + 1)%i. This precomputation can be done in O(N2). With the help of this array, the original can be calculated in O(N3). Also can be optimized to 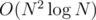 using FFT. Furthermore, since we only concern the answer with S such positions, and every time we are multiplying the same polynomial, so we only need 2 times of DFT, and thus the complexity is O(N2).
using FFT. Furthermore, since we only concern the answer with S such positions, and every time we are multiplying the same polynomial, so we only need 2 times of DFT, and thus the complexity is O(N2).
However, I can't generalize this solution to the case where there are fixed positions, and also I can't find an editorial for this problem. Is there anyone willing to share some insights? Thanks in advance!










By the way, how can I find tutorials to those CSAcademy problems without analysis?
An important condition in the problem is : "For some indices between 1 and N you know the cards of the first player, and for the other indices you know the cards of the second player.", which I have missed initially. ._.
With this condition, the problem can be splitted into two independent subproblems, which is like "Find the number of ways to match a sequence of integers (a1, a2, ..., ak) with (1, 2, ..., k) so that the number of api ≥ i is exactly k".
Sort ai. Now, you can do something like dp[i][j] = number of ways to pair the first i elements so that there are exactly j occurrences of api ≥ i (and not pair the elements with api < i). At the end, you have to multiply dp[k][j] by (k - j)! to pair the remaining elements, but we might overcount the ways to pair the elements so that the number of api ≥ i is more than k, so we should subtract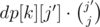 for all j' > j.
for all j' > j.
Thanks! That's of great help.