It turns out that randomly guessing works in Div. 1 too...
I have reached GM thanks to randomly guessing. Ask me anything!
Since I have already argued in theory how randomly guessing helps CF rating, I figured that I might as well compile a list of problems I guessed on my way to GM, to give some empirical evidence to all esteemed grandmasters before my rating falls off. So let us get started!
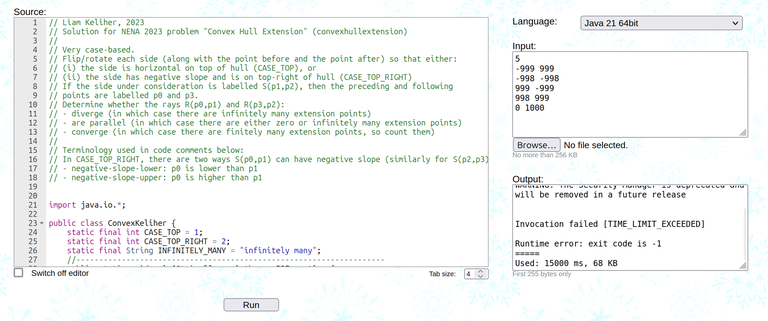
1975D — Paint the Tree
Just solve the problem manually and claim it is the best solution. Surely it is.
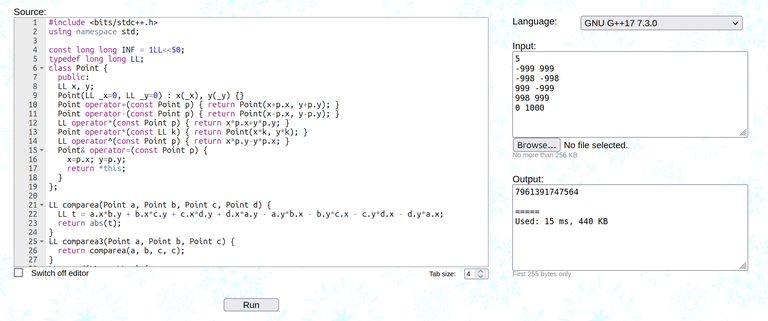
1967C — Fenwick Tree
Have you ever played the game 'find next number in the sequence?'
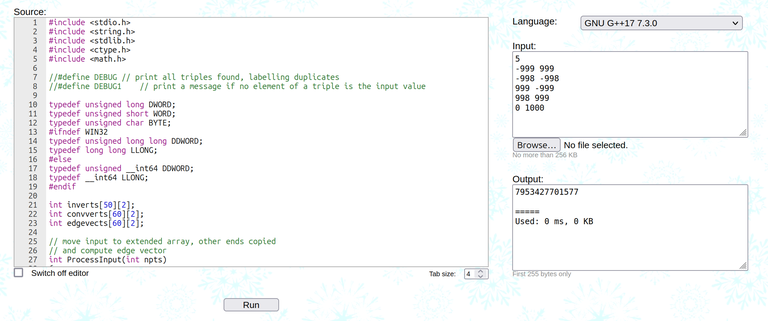
1965C — Folding Strip
- Just fold whenever you can!
- Wait. What if I get stuck somewhere...
- Well... You can always randomly guess that you will never get stuck! Surely that works. Source: Trust me bro
1951
By now you have seen many problems that can be randomly guessed. But have you seen an entire contest that can be randomly guessed?