Zhtluo's blog

Is ICPC ECNA 2023 problem C straight-up wrong?
By Zhtluo, history, 4 months ago, In English

So I was studying this infamous ICPC ECNA 2023 geo problem (https://codeforces.com/gym/104757/problem/C)...

I tried to read the judge's solutions here (https://raw.githubusercontent.com/icpc/na-ecna-archive/main/2023-2024/convexhullextension.zip) from this site (https://na.icpc.global/2022-23/regionals/ecna/ecna-archive-2022-23/) but they don't really make sense to me.

So I came up with this test case:

5
-999 999
-998 -998
999 -999
998 999
0 1000

And I tried to run it on the solutions. It turns out that the solutions don't agree with each other...

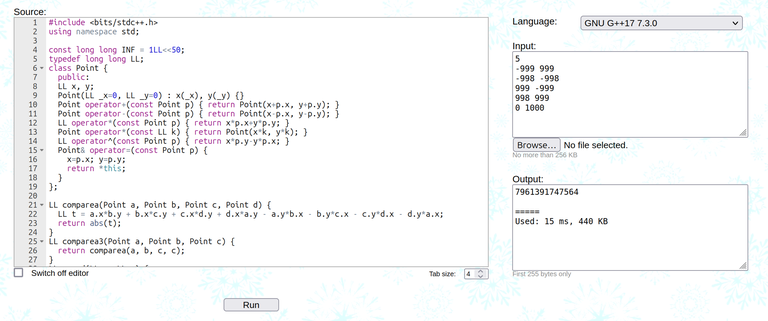
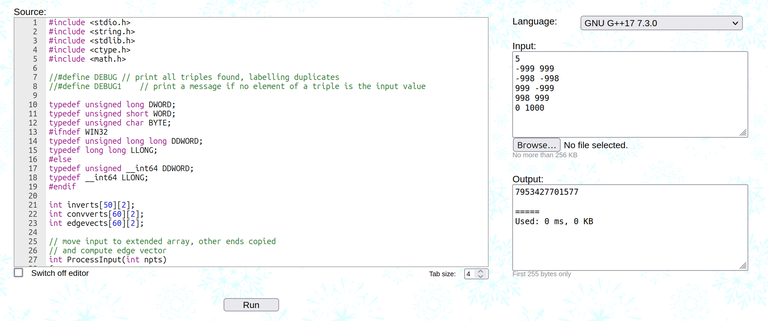
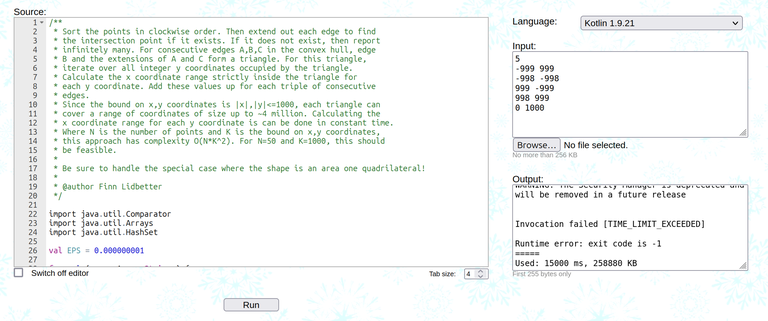
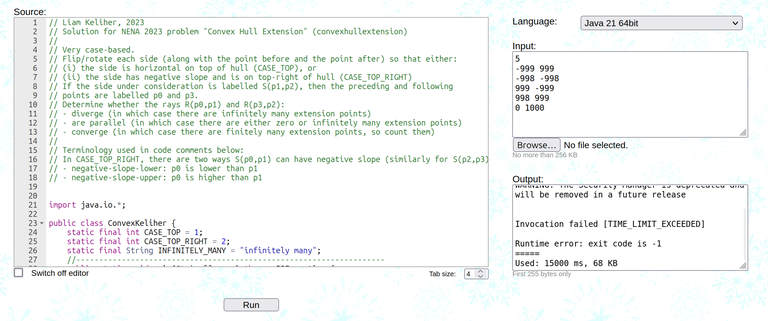
So now I am stumped. What is the correct solution for this problem? Does it even exist?

  • Vote: I like it
  • +182
  • Vote: I do not like it

»
4 months ago, # |
  Vote: I like it +34 Vote: I do not like it

Auto comment: topic has been updated by Zhtluo (previous revision, new revision, compare).

→ Reply
»
4 months ago, # |
← Rev. 3   Vote: I like it +47 Vote: I do not like it

Update: Legendary -14 convinced me that the first solution is correct (Pick's theorem + brute force) and the rest three are wrong.

Still it feels pretty bad that somehow out of four official solutions three are wrong...

→ Reply
  • »
    »
    4 months ago, # ^ |
      Vote: I like it +23 Vote: I do not like it

    Update 2: Upon further investigation (and trying to understand the official solutions) I found that all official solutions fail on this case (TLE):

    5
998 997
0 0
-250 -500
-1 -1000
1000 0
    → Reply
»
4 months ago, # |
← Rev. 2   Vote: I like it +23 Vote: I do not like it

There exists an extension of the Euclidean algorithm that computes $$$\sum_{k=0}^{n-1} \lfloor \frac{ka + c}{b} \rfloor$$$ in $$$O(\log b)$$$ time. With this, the ECNA 2023 C can be solved in $$$O(n \log V)$$$ time. (On the other hand I agree that jury's solutions are all $$$\Theta(V^3)$$$; they also seem to suffer from precision issues when the values become as large as $$$10^9$$$)

The basic idea is to assume $$$2a < b$$$, write $$$\lfloor \frac{ka + c}{b} \rfloor = \sum_{j=0}^{m-1} [ka + c \geq jb]$$$ and change the order of summations to reduce the denominator from $$$b$$$ to $$$a$$$ iteratively. An alternative approach is to use ideas from Problem A: Archiver , which leads to a less simple but more generalized algorithm.

→ Reply
  • »
    »
    4 months ago, # ^ |
      Vote: I like it +10 Vote: I do not like it

    This thing is in my template but I don't know its name in English...

    I think I have a friend who tried this Euclidean thing on the problem and then concluded that the implementation is so hard that he gave up.

    → Reply
  • »
    »
    4 months ago, # ^ |
      Vote: I like it +10 Vote: I do not like it

    djq_cpp How do you solve Archiver? There's no official solution ...

    → Reply
    • »
      »
      »
      4 months ago, # ^ |
        Vote: I like it +18 Vote: I do not like it

      I apologize that the reference to Archiver might not be very accurate (and I did not think about this problem carefully); I was just looking for an early occurrence of the following technique (this is known as something like "Universal Euclidean Algorithm" in the CNOI community and appeared in a problem from the IOI 2022 selection; maybe you're already familiar with it):

      Consider we walk along the segment from $$$(0, \epsilon)$$$ (inclusive) to $$$(a, b + \epsilon)$$$ (exclusive) with sufficiently small $$$\epsilon$$$, during which we write a $$$0$$$ whenever we cross a vertical grid line and a $$$1$$$ when crossing a horizontal grid line. Denote this string by $$$S_{a, b}$$$, e.g., $$$S_{2, 3} = 01011$$$.

      Then, $$$S_{a, b}$$$ can be obtained by replacing each $$$0$$$ in $$$S_{a, b - a}$$$ with $$$01$$$ if $$$a \leq b$$$, or replacing each $$$1$$$ in $$$S_{a - b, b}$$$ with $$$01$$$ when $$$a \geq b$$$. Now, if $$$0$$$ and $$$1$$$ in $$$S_{a, b}$$$ each represent a matrix $$$M_0$$$ and $$$M_1$$$, then the product of $$$M_{T_i}$$$ across $$$T = S_{a, b}$$$ can be computed in $$$O(\log (a + b))$$$ time, using this recursive construction of $$$S_{a, b}$$$.

      I believe that Archiver can be solved using insights from this technique, though: say, we do DP with divide and conquer, and the problem is to complete transitions from $$$[l, m]$$$ to $$$[m + 1, r]$$$ in $$$O(r - l)$$$ (perhaps with a log factor) time. This can be done in linear time because we can simulate the reverse process (i.e., replacing each $$$01$$$ with a $$$0$$$, given that each $$$0$$$ is followed by a $$$1$$$, or vice versa) in the region around $$$m$$$. The operation is deterministic done until some moment the string around $$$m$$$ becomes something like $$$00101011$$$ or $$$1101010100$$$. From this moment, any valid interval containing $$$m$$$ would be almost a prefix of $$$[l, m]$$$ or a suffix of $$$[m, r]$$$, which is much easier to handle.

      On the other hand, I'm unsure whether this is necessary for Archiver (as there exists a geometric solution to https://codeforces.com/gym/103861/problem/K, whose intended solution also uses what I just mentioned).

      (Sorry for my poor English as I'm used to writing CP terms in Chinese...)

      → Reply
»
4 months ago, # |
  Vote: I like it +44 Vote: I do not like it

ECNA/NENA judge here and author of one of the incorrect judge submissions---the Kotlin submission with the incorrect assertion on the upper bound on the number of lattice points.

First of all, thank you for your thorough investigation and my sincere apologies that we fell short in preparing this problem. It is not good enough and I do take it to heart. My motivation for getting involved with helping out in judging was an ICPC contest where two problems were completely broken. So it hurts to hear that problems I helped to prepare are not set appropriately. I will reflect on this to determine what can be done better next time around. One thing I can say immediately is that I wrote that incorrect docstring comment in my kotlin implementation on the upper bound on the number of lattice points and it is a reminder that when judging I should not be content with any non-trivial assertion without formal proof. My assertion there is obviously wrong and I thank you for your simple example demonstrating this. I cannot speak to where the other judges went wrong. I guess we somehow all made a similar incorrect assumption? This is unfortunate.

Regarding the impact on the contest, given that the test data is only incomplete (not incorrect), I think we are lucky in how it worked out on the scoreboard. There was only one team that got AC on the problem (the first place MIT team) and if they had not got AC, the ranking would not have been different. Moreover, this AC submission came after the scoreboard freeze. So as far as I can see, no team benefited from implementing a too slow solution that should not have passed (as all 4 independent judge solutions did) while some other teams, such as Purdue, rightly identified the difficulty and ruled out the simpler approach used by the judges. If we had crafted more complete test data for the specified input constraints (and improved our judge solutions) the effect would have been that at most one judgement in the contest would have changed---possibly changing the first place MIT team's AC to a WA or TLE. But this would have been inconsequential to the rankings. So I think we got very lucky here. Although please correct me if my analysis of the impact on the scoreboard is overlooking something.

Again, my apologies for the incompleteness of the test data. I will be reflecting on what we can do better to avoid this with the resources available. Especially since this issue was not isolated to Problem C... I regret to say that Problem F also suffered from unfortunately incomplete test data; there were submissions during the contest to Problem F that got AC that should have been judged as WA.

→ Reply
  • »
    »
    4 months ago, # ^ |
    ← Rev. 2   Vote: I like it +8 Vote: I do not like it

    Thanks for your comments, and I understand the difficulties that occurred during problem setting.

    Not sure if this is practical for NA, but according to my experience of working for East-Asia Continent regionals, it is usually helpful to get testers of different skill levels to try the problems on their own (often by virtually participating in the contest) before showing them the intended solution. Sometimes, after this, the problem setters would try to hack the testers' accepted solutions. This, as far as I'm concerned, is a necessary procedure for problem-setting in Asia-East. (I don't know if it's true but I heard that what testers in NA care about is mostly to write solutions in different languages, so that every language can pass within the TL). Of course, I believe it also helps by writing formally described and proven tutorials besides passable codes.

    Some personal experience: our first submission to $$$C$$$ is $$$\Theta(V^3)$$$ without careful implementations. We continued to submit after getting AC, aiming to correct our $$$O(n \log V)$$$ code (and figured it out near the end of the competition).

    → Reply
    • »
      »
      »
      3 months ago, # ^ |
        Vote: I like it 0 Vote: I do not like it

      I would not characterise writing solutions in different languages as what testers in NA care about most. It is one element and some effort is made to get at least one passing java/kotlin submission while trying to get prevent worse complexity solutions in C++. But I wouldn't say that it is where most effort is spent. Although that will vary by problem as to how easy or difficult that is to achieve.

      Thanks for sharing your personal experience on problem C. That is impressive to get the $$$O(n \log V)$$$ within the contest!

      → Reply
  • »
    »
    3 months ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    I can certainly help out with testing next time :)

    → Reply
    • »
      »
      »
      3 months ago, # ^ |
        Vote: I like it 0 Vote: I do not like it

      That would be greatly appreciated I am sure! I will reach out by email

      → Reply
»
3 months ago, # |
  Vote: I like it 0 Vote: I do not like it

I also agree with you

→ Reply
»
3 months ago, # |
  Vote: I like it 0 Vote: I do not like it

Can you explain more detail please?

→ Reply
»
3 months ago, # |
  Vote: I like it 0 Vote: I do not like it

I also agree with you

→ Reply
»
3 months ago, # |
  Vote: I like it 0 Vote: I do not like it

I also agree with you

→ Reply
»
3 months ago, # |
  Vote: I like it 0 Vote: I do not like it

I also agree with you

→ Reply