Hello CF community, I was trying to solve this problem 584B - Коля и Таня, I saw that my logic gives wrong answers but I don't know why, my friends' solutions was like find the total cases, subtract the invalid cases but I was thinking of finding the valid cases immediately, here's how I think:
Let's take $$$n=2$$$ for example:
I can either make $$$a_0, a_2, a_4$$$ valid or $$$a_1, a_3, a_5$$$ valid, I know that for every $$$3$$$ vertexes (which are to be valid) I have $$$3^3 - 7 = 20$$$ valid cases, as the invalid cases are:
1. ($$$1, 2, 3$$$)
2. ($$$1, 3, 2$$$)
3. ($$$2, 1, 3$$$)
4. ($$$2, 3, 4$$$)
5. ($$$3, 1, 2$$$)
6. ($$$3, 2, 1$$$)
7. ($$$2, 2, 2$$$)
and for the rest of the vertexes the values I can take are either $$$1, 2,$$$ or $$$3$$$, which means $$$3^{3n-3}$$$ options, so I have $$$n$$$ options ($$$a_0$$$, $$$a_1$$$ in case $$$n=2$$$) with $$$20$$$ valid cases, and for every options of this I have $$$3^{3n-3}$$$ options $$$ \rightarrow $$$ $$$(20\times 3^{3n-3})\cdot n$$$.
Can anyone tell me what's wrong?
→ Pay attention
→ Streams
→ Top rated
| # | User | Rating |
|---|---|---|
| 1 | tourist | 3880 |
| 2 | jiangly | 3669 |
| 3 | ecnerwala | 3654 |
| 4 | Benq | 3627 |
| 5 | orzdevinwang | 3612 |
| 6 | Geothermal | 3569 |
| 6 | cnnfls_csy | 3569 |
| 8 | jqdai0815 | 3532 |
| 9 | Radewoosh | 3522 |
| 10 | gyh20 | 3447 |
→ Top contributors
| # | User | Contrib. |
|---|---|---|
| 1 | awoo | 161 |
| 1 | maomao90 | 161 |
| 3 | adamant | 156 |
| 4 | maroonrk | 153 |
| 5 | -is-this-fft- | 148 |
| 5 | atcoder_official | 148 |
| 5 | SecondThread | 148 |
| 8 | Petr | 147 |
| 9 | nor | 144 |
| 10 | TheScrasse | 142 |
→ Find user
→ Recent actions
Hello CF community, I'm trying to solve this problem, the problem tells me that I have to calculate
in the numerator it will always be $$$\prod _{i = N-M+1}^{n} i$$$ and in the denominator will be $$$ \prod _{i=1}^{min(N, N-M)}i$$$ as the rest will cancel out
and this is my code: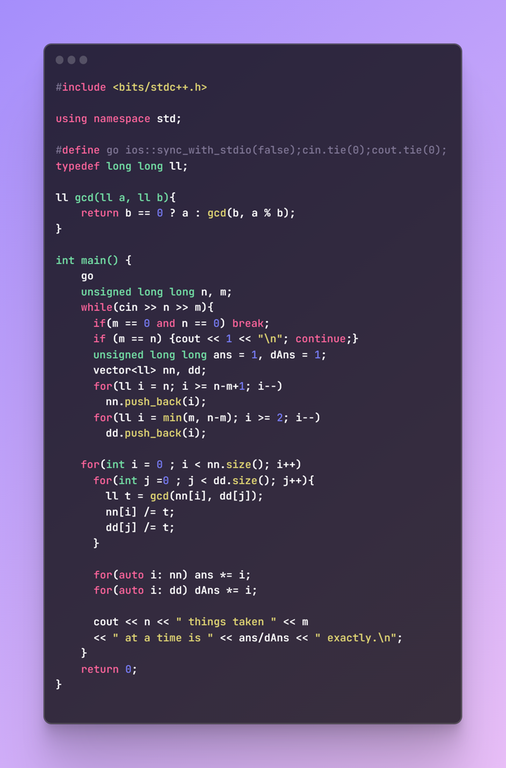
but it gives me WA, I'm not really sure why I'm getting this. Any ideas?
Hello CF community, I'm trying to solve this problem 810B - Summer sell-off, and here's my submission 216849580, Although the code gives AC for the first $$$15$$$ test, it gives a WA on the $$$16$$$-th test, I'm not able to identify the issue, any ideas?. I don't want another solution, I just want to know what's wrong in my solution.
Codeforces (c) Copyright 2010-2024 Mike Mirzayanov
The only programming contests Web 2.0 platform
Server time: Jul/27/2024 07:09:18 (k3).
Desktop version, switch to mobile version.
Supported by
User lists


| Name |
|---|









