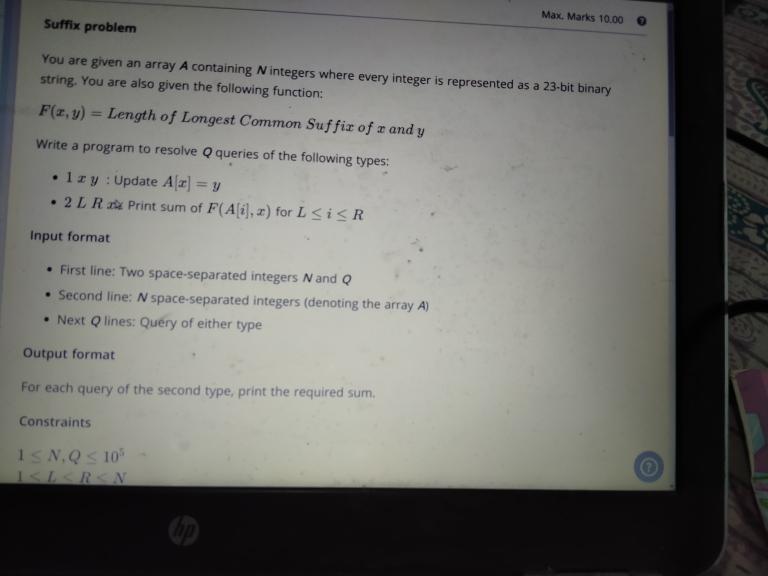
Can anyone explain their solution to any of the last 4 problems.
- Question 3 Apples and Oranges (Contest:16th Feb) Tono is super fond of eating oranges and apples alone, but not so fond of eating them together. Today, she finds that all the 'n' apples and the 'm' oranges that she has are kept in a straight line. As she does not like apples and oranges together, find the expected number of unwanted pairs (adjacent) of apples and oranges if all the arrangements of apples and oranges have equal probability.For example:"O A O A" have 3 unwanted pairs while "O O A A" has 1 unwanted pair.
- Question 4 Min query (contest 16th feb) You are given a rooted tree with N nodes and node 1 as root. Node i initially has a value A[i]. You have to process Q queries on it. Query can be of two type Type 1: Find the minimum element in the subtree of Node X. Type 2: Change all the elements in the subtree of Node X to thier value xor K.
- Question 5 Game of bits (contest 16th feb) F(1,x) = number of set bits in the binary representation of the number x F(k,x) = F(k-1, F(1, x)) ; k > 1 You have to find the number of x for 1 <= x <= N such that the smallest k for which F(k, x) = 1 is C. For example smallest k for x = 1 is 1 x = 2 is 1 x = 3 is 2 x = 4 is 1 x = 5 is 2
Question 6 Tricky Chapo! (Contest: 16th Feb) As always, Sid has come up with a new problem on Number Theory. Since it is too tricky to solve, can you help him. A bonus, you'll get a chapo for solving it right. Given an integer n, let F(n) be the product of all positive integers i less or equal than n such that n and i are co-prime. Now you're given an integer X, you need to find the sum of (F(i) modulo i) for all positive integers i less than or equal to X. If the answer is A, report the value of (A % 1000000007).
The contest has ended