I am attaching a picture about the question. Kindly refer to the picture. 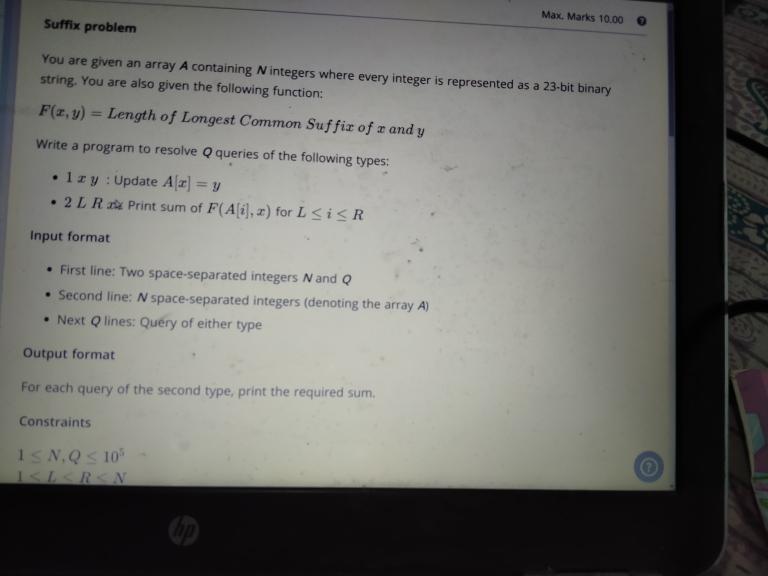
→ Pay attention
→ Streams
→ Top rated
| # | User | Rating |
|---|---|---|
| 1 | tourist | 3947 |
| 2 | jiangly | 3734 |
| 3 | Radewoosh | 3646 |
| 4 | jqdai0815 | 3620 |
| 4 | Benq | 3620 |
| 6 | orzdevinwang | 3612 |
| 7 | ecnerwala | 3581 |
| 8 | Geothermal | 3569 |
| 8 | cnnfls_csy | 3569 |
| 10 | ksun48 | 3479 |
→ Top contributors
| # | User | Contrib. |
|---|---|---|
| 1 | awoo | 162 |
| 2 | maomao90 | 160 |
| 3 | nor | 156 |
| 4 | cry | 155 |
| 4 | adamant | 155 |
| 4 | atcoder_official | 155 |
| 4 | -is-this-fft- | 155 |
| 8 | maroonrk | 153 |
| 9 | Petr | 146 |
| 10 | djm03178 | 144 |
→ Find user
→ Recent actions
↑
↓
Codeforces (c) Copyright 2010-2024 Mike Mirzayanov
The only programming contests Web 2.0 platform
Server time: Aug/24/2024 13:19:29 (h2).
Desktop version, switch to mobile version.
Supported by
User lists


| Name |
|---|










Sample test cases?
You didn't tell us whether the test is finished or not. We shouldn't help you if the test is not finished yet.
It's finished bro.
Reverse all strings, so task becomes about prefix instead of suffix. Create segment tree, where each node have a trie that contains all strings from this node's corresponding segment (each string will be in $$$log~n$$$ tries, so memory will be $$$23 \cdot n~log~n$$$). With trie it's easy to count necessary sum of all string nested in this trie in $$$O(23)$$$, so overall query's complexity will be $$$O(23 \cdot log~n)$$$.
You can do it with a single trie
can you please explain
Basically what you and lemelisk said in the comment below, I'm not sure if it's better, just seems slightly easier to implement
create a trie with reversed strings and store indices of strings in each node in sorted order then query for reversed string, you can find out for each each prefix of reversed string how many strings from given range match this prefix
For updates you will need to store indices in BSTs that supports query "how many elements is smaller than given value". But that a nice alternative to segment tree's solution and it even has lower memory consumption complexity.
I solved it using map and policy based data structure My solution