The editorial is updated.
447A - DZY Loves Hash
We just need an array to store the numbers inserted and check whether a conflict happens. It's easy.
447B - DZY Loves Strings
Firstly the optimal way is to insert letter with maximal wi. Let  {wi}. If we insert this character into the k'th position, the extra value we could get is equal to
{wi}. If we insert this character into the k'th position, the extra value we could get is equal to 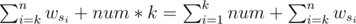 . Because of wsi ≤ num, when k = n + 1, we can get the largest extra value.
. Because of wsi ≤ num, when k = n + 1, we can get the largest extra value.
So if we insert the k letters at the end of S, we will get the largest possible value.
446A - DZY Loves Sequences
We can first calculate li for each 1 ≤ i ≤ n, satisfying ai - li + 1 < ai - li + 2 < ... < ai, which li is maximal.
Then calculate ri, satisfying ai < ai + 1 < ... < ai + ri - 1, which ri is also maximal.
Update the answer 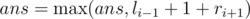 , when ai - 1 + 1 < ai + 1.
, when ai - 1 + 1 < ai + 1.
It's easy to solve this problem in O(n).
446B - DZY Loves Modification
If p = 0, apperently the best choice is choosing the row or column which can give greatest pleasure value each time.
Ignore p first,then we can get a greatest number ans. Then if we choose rows for i times, choose columns for k - i times, ans should subtract (k - i) × i × p.
So we could enumerate i form 0 to k and calculate ansi - (k - i) * i * p each time, max {ansi - (k - i) * i * p} is the maximum possible pleasure value DZY could get.
Let ai be the maximum pleasure value we can get after choosing i rows and bi be the maximum pleasure value we can get after choosing i columns. Then ansi = ai + bk - i. We can use two priority queues to calculate ai and bi quickly.
446C - DZY Loves Fibonacci Numbers
As we know, 
Fortunately, we find that 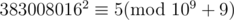
So, 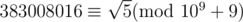
With multiplicative inverse, we find,
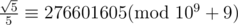
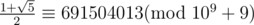
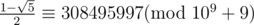
Now, 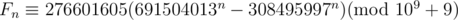
As you see, we can just maintain the sum of a Geometric progression 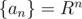
This is a simple problem which can be solved with segment tree in 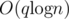 .
.
446D - DZY Loves Games
Define important room as the trap room. Let w(u, v) be equal to the probability that DZY starts at u (u is a important room or u=1) and v is the next important room DZY arrived. For each u, we can calculate w(u, v) in O(n3) by gauss elimination.
Let Ai be equal to the i'th important room DZY arrived. So Ak - 1 = n, specially A0 = 1. Let ans be the probability for DZY to open the bonus round. Easily we can know 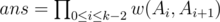 . So we can calculate ans in
. So we can calculate ans in 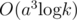 (a is equal to the number of important rooms) by matrix multiplication.
(a is equal to the number of important rooms) by matrix multiplication.
So we can solve the problem in  . we should optimize this algorithm.
. we should optimize this algorithm.
We can find that each time we do gauss elimination, the variable matrix is unchanged. So we can do gauss elimination once to do preprocessing in O(n3). Then for each time calculating w(u, v), the only thing to do is substitute the constants. In this way we can calculate w(u, v) in O(n3).
In this way, we can solve this problem in 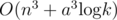
446E - DZY Loves Bridges
Let n = 2m. For convenience, we use indices 0, 1, ..., n - 1 here instead of 1, 2, ..., n, so we define a0 = an.
Obviously this problem requires matrix multiplication. We define row vector 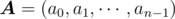 , and matrix
, and matrix 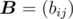 , where bii = 1,
, where bii = 1, 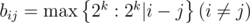 . The answer is row vector
. The answer is row vector  .
.
Since n can be up to 3 × 107, we need a more efficient way to calculate. Let 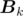 denote the matrix
denote the matrix 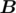 when m = k. For example,
when m = k. For example, 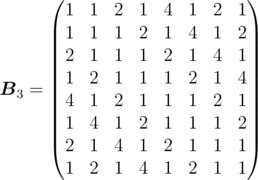
Define 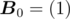 , then we can easily find that
, then we can easily find that
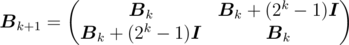
where 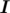 denotes the identity matrix.
denotes the identity matrix.
For an n × n matrix 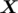 and a constant r, we can prove by induction that
and a constant r, we can prove by induction that 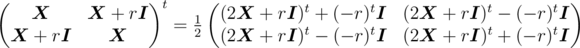
Let α1, α2 be two 1 × n vectors, then we have 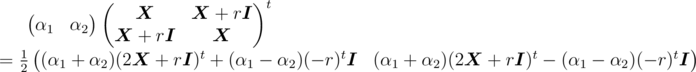
This result seems useful. Suppose we want to find 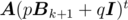 , where
, where 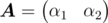 , we have
, we have
 so we just need to find
so we just need to find 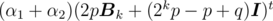 , which is a self-similar problem. By recursion, it can be solved in time T(n) = T(n / 2) + O(n) = O(n).
, which is a self-similar problem. By recursion, it can be solved in time T(n) = T(n / 2) + O(n) = O(n).










