The editorial is updated.
447A - DZY Loves Hash
We just need an array to store the numbers inserted and check whether a conflict happens. It's easy.
447B - DZY Loves Strings
Firstly the optimal way is to insert letter with maximal wi. Let  {wi}. If we insert this character into the k'th position, the extra value we could get is equal to
{wi}. If we insert this character into the k'th position, the extra value we could get is equal to 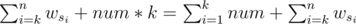 . Because of wsi ≤ num, when k = n + 1, we can get the largest extra value.
. Because of wsi ≤ num, when k = n + 1, we can get the largest extra value.
So if we insert the k letters at the end of S, we will get the largest possible value.
446A - DZY Loves Sequences
We can first calculate li for each 1 ≤ i ≤ n, satisfying ai - li + 1 < ai - li + 2 < ... < ai, which li is maximal.
Then calculate ri, satisfying ai < ai + 1 < ... < ai + ri - 1, which ri is also maximal.
Update the answer 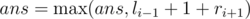 , when ai - 1 + 1 < ai + 1.
, when ai - 1 + 1 < ai + 1.
It's easy to solve this problem in O(n).
446B - DZY Loves Modification
If p = 0, apperently the best choice is choosing the row or column which can give greatest pleasure value each time.
Ignore p first,then we can get a greatest number ans. Then if we choose rows for i times, choose columns for k - i times, ans should subtract (k - i) × i × p.
So we could enumerate i form 0 to k and calculate ansi - (k - i) * i * p each time, max {ansi - (k - i) * i * p} is the maximum possible pleasure value DZY could get.
Let ai be the maximum pleasure value we can get after choosing i rows and bi be the maximum pleasure value we can get after choosing i columns. Then ansi = ai + bk - i. We can use two priority queues to calculate ai and bi quickly.
446C - DZY Loves Fibonacci Numbers
As we know, 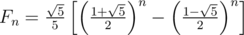
Fortunately, we find that 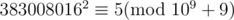
So, 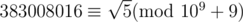
With multiplicative inverse, we find,
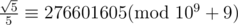
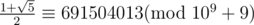
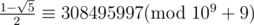
Now, 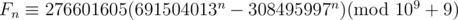
As you see, we can just maintain the sum of a Geometric progression 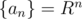
This is a simple problem which can be solved with segment tree in 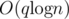 .
.
446D - DZY Loves Games
Define important room as the trap room. Let w(u, v) be equal to the probability that DZY starts at u (u is a important room or u=1) and v is the next important room DZY arrived. For each u, we can calculate w(u, v) in O(n3) by gauss elimination.
Let Ai be equal to the i'th important room DZY arrived. So Ak - 1 = n, specially A0 = 1. Let ans be the probability for DZY to open the bonus round. Easily we can know 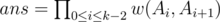 . So we can calculate ans in
. So we can calculate ans in 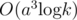 (a is equal to the number of important rooms) by matrix multiplication.
(a is equal to the number of important rooms) by matrix multiplication.
So we can solve the problem in 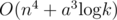 . we should optimize this algorithm.
. we should optimize this algorithm.
We can find that each time we do gauss elimination, the variable matrix is unchanged. So we can do gauss elimination once to do preprocessing in O(n3). Then for each time calculating w(u, v), the only thing to do is substitute the constants. In this way we can calculate w(u, v) in O(n3).
In this way, we can solve this problem in 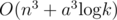
446E - DZY Loves Bridges
Let n = 2m. For convenience, we use indices 0, 1, ..., n - 1 here instead of 1, 2, ..., n, so we define a0 = an.
Obviously this problem requires matrix multiplication. We define row vector 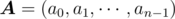 , and matrix
, and matrix 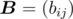 , where bii = 1,
, where bii = 1, 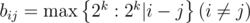 . The answer is row vector
. The answer is row vector 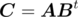 .
.
Since n can be up to 3 × 107, we need a more efficient way to calculate. Let 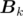 denote the matrix
denote the matrix  when m = k. For example,
when m = k. For example, 
Define  , then we can easily find that
, then we can easily find that
where 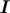 denotes the identity matrix.
denotes the identity matrix.
For an n × n matrix 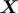 and a constant r, we can prove by induction that
and a constant r, we can prove by induction that 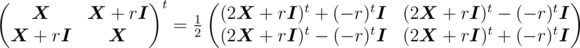
Let α1, α2 be two 1 × n vectors, then we have 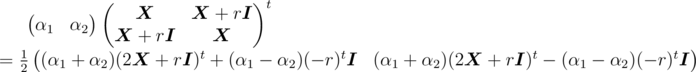
This result seems useful. Suppose we want to find 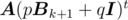 , where
, where 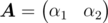 , we have
, we have
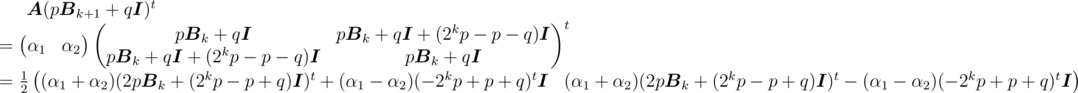 so we just need to find
so we just need to find 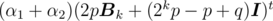 , which is a self-similar problem. By recursion, it can be solved in time T(n) = T(n / 2) + O(n) = O(n).
, which is a self-similar problem. By recursion, it can be solved in time T(n) = T(n / 2) + O(n) = O(n).











I think I found this editorial first!
Well done!
wow so fast Editorial.. such a hard round..
nobody solved Div-1 E. did u have to go and make the explanation so scary? :D
well……it is very common that no one solve a Chinse Round Div1E…… :D
I have a small query in 446A — DZY Loves Sequences question.
For the input :
3 5 1 2
The output should be 2 because the value should be strictly > 1 right ?
But in the test cases, it is given 3. Why?
For example 3 5 8 2
Change 5 to 0, or some negative integers ...
negative numbers are still integers.
You can change 5 to 0.
Problem statement says that the replaced number can be any integer not positive integer.
So, this sequence can be transformed into 0 1 2 and thus the answer is 3.
Replaced number is ANY integer, ah! No wonder I was getting WA repeatedly.
I looked at the range of inputted integers (1<=ai<=10^9) and assumed that the replaced integer falls in that range as well.
Is there anybody who solved Div1C in that way?
I didn't code, but I came up with that.
I solved it in the way the same as the editorial. my submission..7085786 and I have found use Segment Tree to maintain Matrix can get ac too. for example:7084920
Another way to solve Div1 C would be to use a sparse table. Let dp[i][l] be the sum of fibonacci numbers from range i to i+(2^l)-1. This can be precalculated in nlog(n). Sum for any range l-r can now be calculated in log(n).
This is followed by segmented tree with lazy propagataion for each query. Time complexity for each test case is q*log(n)^2.
This is the simplest/easiest solution I could think of.
did you solve it in that way? I would like to see your code.
its better to build an array of fibonacci sum from 1 to i, O(N) memory instead of O(N logN).
I implemented a segment tree with lazy updates but I always got TLE. (7087584
Sorry I misunderstood the problem which messed up my thinking. Forget about what I said.
No, your solution should work. It's just that you don't need a sparse table (but you can work with it) and the hard part of the solution is the lazy propagated segment tree.
Xellos, can you tell me why my solution is too slow?
Instead of trying to decipher a Java code (it's an alien language to me :D), I'd take a guess that your lazy updates aren't implemented well and actually take O(interval size) and not O(1) for updating a vertex containing that interval. Your code takes 3 seconds on N = 104, from which you can guess that something's extremely wrong.
I gonna check that, my implementatigor AC in spoj (Horrible queries) but I may made a mistake while editing it.
thanks.
Or weak cases in that problem. Or something. Anyway, if it takes 4 seconds on 10x smaller inputs than max, it can't be ok asymptotically.
Uh... the editorial for C is way too much magic. There are simpler solutions, if we just use general Fibonacii sequences (starting with a, b). Then, using matrix multiplication, we can compute the coefficients ca, cb of the k-th element of this sequence (aca + bcb) and sa, sb of the sum of the first k elements (asa + bsb). The rest is just a standard lazy-loading interval tree (e.g. segment tree with lazy propagation), where we just remember that we want to add to the whole interval of vertex v sequences with sums starting with v.a, v.b, the sum in this interval, and are able to compute the changes in sum and what the k-th elements of this sequence will be.
Code: 7092191. Works comfortably in less than a second.
Btw:
We can do this without matrix multiplication:
1) F(a, b, k) = a * fk - 2 + b * fk - 1 -- k-th element of general Fibonacii sequences starting with a, b, where fi — i-th Fibonacci numbers (starting from 1, 1).
2) sum of first k members of general Fibonacci sequence Fi equals to Fk + 2 - F2.
So we only need to precalculate Fibonacci numbers.
Yeah, I know. Still, I think using matrix multiplication is kind of closer to a programmer's mindset and writing it takes about as much time as checking if you've got the exactly correct formulas (which I didn't, that's why I didn't even bother writing them :D).
Can you explain, please, solution with lazy segment tree? I can't understand how we should recalculate a[l] .. a[r] with O(log(n)) time, I know how to lazy add a one number to every element in segment with O(log(n)), but i can't understand how to add different numbers to elements in segment with O(log(n)).
Check my code for exact formulas; the idea is that if we add to the same interval a Fibonacci sequence starting with a1, b1 and another sequence starting with a2, b2, then it's the same as adding a sequence starting with a1 + a2, b1 + b2, and that's the same as adding (for a matrix A, whose powers I compute as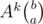 (it's a vector, not a binomial coefficient) to the k-th element of this interval. This also allows us to know what this sequence looks like from the c-th (not 0-th) element: it's just a Fibonacci sequence starting with
(it's a vector, not a binomial coefficient) to the k-th element of this interval. This also allows us to know what this sequence looks like from the c-th (not 0-th) element: it's just a Fibonacci sequence starting with 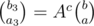 . Using this property, we can convert a sequence (given by its first 2 elements) that's added to an interval into 2 sequences (also given by first 2 elements) that are added to 2 subintervals, which forms the basis of lazy propagation. Using precalculated
. Using this property, we can convert a sequence (given by its first 2 elements) that's added to an interval into 2 sequences (also given by first 2 elements) that are added to 2 subintervals, which forms the basis of lazy propagation. Using precalculated 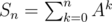 , we can easily calculate the sum of any Fibonacci sequence just based on its first 2 elements.
, we can easily calculate the sum of any Fibonacci sequence just based on its first 2 elements.
pw[]) the bottom element ofThanks a lot. I think that i understood your solution :)
Amazing solution, thanks a lot :P
why can't we just keep the cumulative sum modulo in the fibonacci array ?
I mean like Ai = (Ai-1+Ai-2)mod p . and then each query we add (Ar-Al+1)%p to the segment tree. ?
I'm not sure what you mean, and I think if you didn't just write "add [constant] to the segment tree", I'd understand it better. Maybe your idea is the same as what I wrote, just with Fibonacci numbers instead of matrices (whose elements are Fibonacci numbers, anyway).
No , I meant that I generate all the Fibonacci numbers modulo from 1 to 3000005. so , I have got this Fibonacci array fib , where fib[i] = (fib[i-1]+fib[i-2]) % 100000009. now I create another array cumulative Fibonacci , cumfib , where cumfib[i] = (cumfib[i-1] + fib[i])%1000009
Now , when we got a query l,r on the segment tree for values l...r , we just add cumfib[r]-cumfib[l] to the interval l...r of the tree. Will this work ?
You're wrong. Suppose you had an array of size 2 and an "add" query on the interval [1,2]. Your cumfib[] should be 2 (as F1 + F2), so you'd add 2 to the interval [1,2]. But if you then had to find the sum from interval [1,1], how would you do that? You only know that you added 2 to [1,2], but not what sequences formed it.
You're probably missing the whole concept of segment trees with interval updates and queries.
yeah , I understand now... thanks! but can you please explain your soln a bit more? I mean what are a,b and ca,cb ?
a, b are the first and second element of the sequence and ca, cb, sa, sb are just some coefficients (obtained by matrix multiplication, I don't want to just rewrite the formulas from my code, but you can try yourself that they produce the desired results... or just google something about how Fibonacci numbers work with matrix multiplication). There are 2 main and well known concepts here: using matrices to compute Fibonacci numbers and lazy-loading interval tree (lazy propagation segment tree), the rest is mostly about rewriting the formulas into the code correctly.
My solution here http://codeforces.com/contest/446/submission/7094142 is without matrix operations. It just uses standard identities for summing fibonacci numbers.
Deleted, wrong place (a few comments too high) and time (3 at night) to post...
Hi Xellos, I think this approach might work if we propagate to children more carefully!! I tried my best to implement but ,stuck with a bug Please take a look at my submission here:14316365
Xellos You know what you are simply awesome. Your code , your explanation everything. you are an asset to this community... Thanks for your life saving short and effective editorial for this awesome problem.
yeah ... really big thanks from me too.... Just awesome ..
Is it possible to solve it using square-root decomposition? I tried it and it is giving memory limit exceed as it should. The space complexity of square-root decomposition is O(nsqrt(n)). Can we improve on it and solve using this method?
Solved it using square root decomposition with $$$O(n\sqrt{n})$$$ time and $$$O(n)$$$ memory. The submission is here, 155232894
The simpler approach for Div. 1 C using square root decomposition:
Let's divide the array into $$$\sqrt{n}$$$ smaller blocks of size $$$\sqrt{n}$$$. For each query, we will iterate through the list of the blocks. Let $$$sum[i]$$$ be the sum of elements of the $$$i$$$-th block.
For the first type of query,
If the $$$i$$$-th block is completely outside of the update range, just skip it.
If the $$$i$$$-th block is completely inside the update range and we need to add $$$x$$$-th and $$$y$$$-th fibonacci numbers with the first and the last element of the block respectively, update the value of $$$sum[i]$$$ with the sum of $$$x$$$-th to $$$y$$$-th fibonacci numbers (precalculate the prefix fibonacci sum). Store the value which will be added with the first two elements of the block (it will be used later).
If the $$$i$$$-th block partially intersects with the update range (at most two such blocks exist of this type), manually update each element of the block (which is inside the update range) and the value of $$$sum[i]$$$.
For the second type of query,
If the $$$i$$$-th block is completely outside of the query range, just skip it.
If the $$$i$$$-th block is completely inside the query range, add $$$sum[i]$$$ with the answer.
If the $$$i$$$-th block partially intersects with the update range, first update each value of the block iterating over the block (use the stored value which will be added with the first two elements of the block to update the next values). Then manually add the value of each element that is inside the query range.
Complexity $$$O(q\sqrt{n})$$$ for time & $$$O(n)$$$ for space.
My submission: 155232894
"As you see, we can just maintain the sum of a Geometric progression .
This is a simple problem which can be solved with segment tree in O(q log n)."
Hm, I came up with that reduction and with maintaining the sum of a geometric progression, but I definitely won't call that maintaining easy. Btw that solution exists, because square root of 5 mod 1e9 + 9 exists, but it can still be done by some standard operations on matrices (assuming we already know how to maintain sum of a geo progression) even if 5 is a quadratic nonresidue.
Incorrect, deleted.
Wasn't that comment meant to be a reply to Xellos' comment above?
Yeah, may be :)
This was nice (AC before System Test) :
+1 for Proofathon
In Div1C, Fn=sqrt(5)/5*(((1+sqrt(5))/2)^n - (((1-sqrt(5))/2)^n)) so Fn should be 276601605*(691504013^n - 308495997^n).
In div. 1 C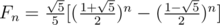 so Fn should be 276601605 * (691504013n - 308495997n).
so Fn should be 276601605 * (691504013n - 308495997n).
Thank you for decoration. I did not find how to use tex markup here.
You write math the same way you'd do it in any TeX document: put the formulas in
$.Put your formula inside the $$
Thank you author of this editorial for making that mistake :)! I just won 20zł (zł is currency in Poland) with Marcin_smu thanks to that.
He asked me which one of those two possible values of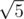 he should choose (of course if there is at least one then there are exactly two of them). I replied that it doesn't matter, because only property of
he should choose (of course if there is at least one then there are exactly two of them). I replied that it doesn't matter, because only property of 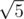 mod 109 + 9 is that its square is 5. He replied that if we will take second value instead of first, we will get negated sequence and offered me a bet. I looked at that formula in editorial and it convinced me even more, because I noticed that it is very probable that he thought like that because of that typo in editorial and agreed to the bet. And it was exactly as I suspected :D.
mod 109 + 9 is that its square is 5. He replied that if we will take second value instead of first, we will get negated sequence and offered me a bet. I looked at that formula in editorial and it convinced me even more, because I noticed that it is very probable that he thought like that because of that typo in editorial and agreed to the bet. And it was exactly as I suspected :D.
That was a bit confusing @@. So we can choose both values of sqrt(5) ?
Yyy, yes, I just explained that. We don't need anywhere exact value of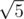 . It's not important that its decimal representation is sth like 2.2 and it's not important that mod 109 + 9 it can be 383(...) but one thing which is important is that its square is 5.
. It's not important that its decimal representation is sth like 2.2 and it's not important that mod 109 + 9 it can be 383(...) but one thing which is important is that its square is 5.
About the answer to 446B, can somebody please explain this to me:
"Ignore p first,then we can get a greatest number ans. Then if we choose rows for i times, choose columns for k - i times, ans should subtract (k - i) × i × p."
What does it mean to ignore p first? Isn't it important what rows and columns we are choosing? Why?
The effect of p is constant on all rows and columns ... It just depends on how many row operations you make out of the k operations.
For Div2. C. how can we calculate Li and Ri for all i in linear time?
u can do this using dynamic programming.
if u want the exact implementation, u can see my solution 7077771.
Thanks!
How can we came up with such solution of Div 2C problem? What is first step for such problems? Maybe that is easy but it seems tricky magic for me
Can someone explain this issue, please?
First of all , you know you can change only one number. So why not try each number for 1 to n and see if I can change this what is the value.
Now suppose you are at index i. Now the thing is , you need to know how far the decreasing goes at the left of i. for example , 12 2 3 5 1 9 , you see for i= 4 , we get 5,3,2 that is 3 length, Similarly you have to catch at right which is only 9. And now to see if you can change the value. the difference between i-1 and i+1 i.e 5 and 9 is 4 , so you can insert a number such as 6,7 or 8 there and make the sequence increasing . Now the length of the sequence is (2,3,5)->l[i] + (9)->r[i] + 1. so you take maximum of all this and you get the ans.
Now , how to calculate l[i] and r[i] ? you see , you iterate through 1 to n , now for each i , if A[i] > A[i-1] , we can increase the sequence, so A[i] = A[i-1]+1. else we start a new sequence and A[i] = 1. similar for r[i] but iterate from n to 1. Hope it clears.
Thank you. It's clear right now. I used the similar idea in my solution but I used one iteration through 1 to n.
Can someone please explain DIV2-D DZY loves modification? The editorial is so short and brief I can't find a clue what's going on.
We can consider the rows and columns separated. It's easy to get the largest value of choosing k rows and the largest value of choosing k columns. Then consider if we choose a row after choosing a columns. The answer should be subtract by a * p. Then for a operation sequence of choosing rows for i times and columns for k - i times. If we swap two operations, the total number which should be subtract doesn't change. So we can calculate the total number should be subtract is i * (k - i) * p. So we can enumerate i and solve this problem.
Test cases for Div1B/Div2D are weak.
Solution 7093794 uses int instead of long long for row/column sums (in order to fit into TL with O(k * (n + m))).
For test
it gives answer 8418438592 because of overflow. It is clearly wrong, because every operation on such array will give <=0 additional happines (and correct answer for this test is -48747930000).
upd. problem statement says ar[i][j]>0, my first example is not valid. We may change matrix of 0's to matrix of 1's, and for this test we'll have 9406338592 instead of -48746942100.
upd2. i've read some random solutions from contest. gchebanov, flashmt have this bug (and most probably few others).
I'm sorry for our mistake. T^T
I wonder why there is no rejudge? It's not an ACM contest, so it didn't actually change anything for these guys.
D: Am I tight that if all (except the first one) rooms are with traps than solution works in just O(n^3 log k)? My O(n^3 log k) was too slow:(
The number of the trap rooms is no more than 100.
Oh, I didn't notice that:(, sorry
Hey. I misunderstood condition second task decided to try the greedy algorithm tried passed. I have a question for the problem in Example abc 3 1 2 2 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 if the answer to take letters, could receive only «abcbbc»??? or could even «abcbbb»? thanks for the earlier
In this case both strings are valid. Note that wb = wc = 2.
You know, resizing is possible if you put the image in html tags.
But these formulas are worthy even of nope.avi
I haven't read that, but I will probably enjoy that problem, but sometimes I wonder why they put such tasks in contest which lasts 2 hours. It is clearly wasting interesting problem, because nobody will be even close to solving it :(.
hahaha) that's my reaction)
Surprisingly enough, the solution is very easy to code. Maybe one could derive these formulas in an hour or two, but there is no way one could have that much time left after solving the 4 previous problems.
Welcome to China.
Fortunately, we find that 3830080162 = 5(mod109 + 9)
How did we find this number ?
Firstly:
1) Wolframalpha
or
2) Bruteforce (note that program finding that number doesn't have to output answer in 2s).
Secondly:
Hardcode
Why do we need this observation for Fibonacci problem? i simply precomputed first 300 000 Fibonacci numbers in an array.
In order to reduce the problem to a sum of geometric series, as apparently it makes it easier to solve. My solution doesn't use that either, here's roughly what I did:
We need to be able to find the sum Sk = A1... Ak (the answer to the second query is Sr - Sl - 1)
First, we precompute partial sums for the initial array at the beginning
Then, we need to include the Fibonacci segments that fully lie within range (1, k) — this is done with a simple segment tree once we have precomputed FSk = F1... Fk
Now, we need to include segments that partially lie within our range. For this, we extend the segments to the left until the beginning of our array (Fibonacci sequence can be extended to the left using Fk - 1 = Fk + 1 - Fk), and use two segment trees to find the sum of the elements that appear at the first and second positions in our array. Since Fibonacci sequences are additive (assuming Fa, b is a sequence that begins with a, b, we have Fa, b + Fc, d = Fa + c, b + d), we now need to find the sum of the first k elements of a sequence beginning with those two numbers, which can be done by precomputing coefficients for the first two elements. Don't forget to subtract the sum of the negative Fibonacci elements from the resulting sequence (these values can be included in the first interval tree).
But when we have fixed size static values we don't need this optimization. I used an array with the prefix sums of the Fibonacci numbers up to 300010 and I can find the sum of any interval in constant time.
I did not finish my problem because I spend too long trying to challenge, but I believe it should work. I used bucketing in 548 buckets of size 548. Each query would only perform in the order of 548 operations which should be fast enough I think,
As I said, it is definitely possible to solve the problem directly, its just a different solution from the one mentioned in the editorial.
I'm not sure what you do with buckets — for buckets fully covered by the "add" query, I suppose you simply maintain the first two elements, and for end buckets you add the values directly to the original array?
Exactly.
I just tried writing a solution with buckets, I'm getting TLE on the maximum test (300000 N/M and all queries span almost the entire array takes about 5-6 seconds). My submission is 7103071, I don't see how it can be improved without using interval trees.
Nice :-) My draft was way longer. 5-6 seconds it's motivating because it seems it can be optimized enough. I would try to avoid ',' operator.
Its great for squeezing several small operations inside an if/for without using {}, which sometimes makes it more readable (though with the way I used it here it probably doesn't really help with readability). Problem is, the small optimizations like not using division inside the loop are probably done by the compiler anyway. Changing
BUCKETto 512 should auto-optimize the modulo with & but it doesn't make it much faster.You may try some other solution with working time.
working time.
Lets divide queries by blocks of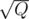 size (or even
size (or even 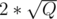 for a little bit faster solution). Then for every update query you just remember "i'll have to do that update later", and for sum query you first take old value of partial sums, and then for every update that you still have to do — intersect it with your sum query range and add required fibonacci partial sum to your answer. At the end of every block just do all updates that you need in O(N) (moving from left to right over your array) and update partial sums.
for a little bit faster solution). Then for every update query you just remember "i'll have to do that update later", and for sum query you first take old value of partial sums, and then for every update that you still have to do — intersect it with your sum query range and add required fibonacci partial sum to your answer. At the end of every block just do all updates that you need in O(N) (moving from left to right over your array) and update partial sums.
This solution works 2-3 seconds and passes TL without any problems. Here is mine: 7087032
It's really a hard round.(a math round again?) congratulations to the winners and thanks to DZY!
It seems that tests for Div1 D are weak, for test
this AC solution 7089186 gives 0.5 which is wrong. Other AC solutions, for example this 7086133, gives 0.3333333.
Could somebody explain more clearly the author's solution for Div1B?
I had the following idea: Store the sums for rows and columns in two heaps. Every time I choose a row, that row's sum will decrease by n * p and every column's sum will decrease by p.
For each of the k steps I choose the maximum from the heaps. Suppose the maximum value is a column. I add its value to the answer, update it, and substract p from every line. The substraction from every line is done in O(1) using an auxiliary variable (substract_row in my code).
I get WA on test 4. My code is here: http://codeforces.com/contest/447/submission/7102900.
Your solution is greedy — it is not optimal to always choose the row/column with the largest sum.
The correct solution splits the problem into two parts. First, we try to solve it for different values of K using only rows, then only columns (both can be done greedily, like you suggested), and save the results.
Then we choose all values of R from 0 to K and try to combine the solutions that use R rows and K - R columns. The key observation is that the relative order of rows and columns doesn't matter — in any case, for each row-column pair whichever comes first will reduce the result of the other one by exactly p, so the answer will be
AnsRow[R] + AnsCol[K-R] + R * (K - R) * p.It is OK to take X best row moves and Y best column moves using greedy approach, if you have fixed X and Y. But for given K greedy approach may give not the best partition of K into X and Y. Here is counterexample:
Author's solution calculates 1, 2, 3,... k best moves on rows/columns, and then try all possibilities: do only k row moves, do k-1 row moves and 1 column move, do k-2 row moves and 2 column moves and so on.
Thank you both! The test case explained very well what I was doing wrong. I finally got accepted. :)
Just thought I'd mention, it seems you forgot to multiply the character weight by the character position in the string in the explanation for Div2.B.
may someone make a detailed explanation of the solution for problem Div1 D?
First, we need to reduce the graph. For each room A and a trap room B calculate the chance that the next trap room after A will be B. For a given B, we can make a list of equations for those values and solve them via Gauss elimination. For example, in the example case, let's find the probability that the room #3 will be next. P3(1) = P3(2), since there is nowhere else to go from room 1, and neither of those rooms are trapped. P3(2) = 2 / 3P3(1) + 1 / 3, because we can either go back to room 1 or forward to room 3. P3(3) = 1 / 2P3(2) + 1 / 2P3(4). P3(4) = 1 / 2. P3(5) = P3(4).
Once we have calculated these values, we can construct a new graph that contains only the first room and all trap rooms, and use the computed probabilities as the edges in the new graph. Now we need to calculate the chance that we will end up in room N after K-1 moves. This can be done with matrix multiplication: let V be a vector such that Vi is the probability that we are currently in room i, and let P be the matrix of probabilities we computed previously. Then, P·V is a vector of new probabilities after one step. Which means that to find the answer, we need to calculate Pk - 1·V. Raising a matrix to power of k can be done in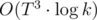 , where T is the number of trap rooms, which is not higher than 100 (plus one).
, where T is the number of trap rooms, which is not higher than 100 (plus one).
The last complication is that Gauss elimination is O(N3), and we need to run it up to 100 times, which is too slow. This is solved by noticing that the matrix on the left hand side is always the same, and only the right hand side values change. So we can use Gauss elimination once to find the inverse of that matrix, and then use it to find the probabilities for every right hand side vector in O(N2).
Hah, in course on Computational Math at my university I was taught that finding inverses of matrices is a crime on numerical correctness :P. What Gauss elimination gives us is a PLU = A representation of matrix A, where P is a matrix of permutation, L is a down-triangle matrix and U is an upper-triangle matrix. Then, when we want to solve equation Ax=b with fixed A and given b, we can do it by solving consecutively Pc = b, Ld = c, Ux = d :P. However I will be curious if there was ever a case such that finding inverse got bad numerical properties and such solution was demanded to fit answer into wanted precision :P.
It is probably not the best idea to find the inverse of a real-valued matrix but it seems to work in this case. You suggest not finding the full inverse, but instead leaving it at LU decomposition in order to improve precision?
I wonder if its possible to make a test that would really force some significant precision loss out of this.
My lecturer suggests (or even insists :P) not finding inverses and so I am, but I guess that for contest's purposes finding inverse will be sufficient in >=95% of cases, so profits resulting from that PLU factorization are probably too small to give a %&*^ about this :P.
Interesting.. I made a test with N=5, M=10^5, K=10^9, only the last room is trapped, and all edges are chosen randomly, and every accepted solution I tried printed something like 0.9992 (the correct answer is obviously 1).
Weak tests eh?
You don't really need to find the inverse, you can simply do GEM with a matrix as the right side of the augmented matrix (instead of just a vector).
I don't see how inverses could be so imprecise, though, since they can also be found using GEM.
"Because computing inverse is not numerically correct"
It does what we want just as well as GEM does, since we can compute inverses using GEM. How is that not numerically correct?
Is the inverse the probability from w to v? If is so,why is it?
what's the right hand side vector?
I need help with 446B. Here's my code: 7118091
My approach is the following.
I get WA on the 4th test, it's too big for me to analyse it (I can't even get access to the full example), nor I can get access to the full test data. Would this approach satisfy the time limits, and where is my mistake?
I_love_Tanya_Romanova explains why this approach does not give the optimal result some comments above yours. Also, he posted a small counterexample.
Can anyone please elaborate the reasoning behind the solution of DIV2 DZY Loves Sequences. The solution works but I don't understand why?
I have a problem in 446A — DZY Loves Sequences. I have found a tricky test data: 7, 1000000000,1 . According to the description, the segment sequence must be strictly increasing and thus we cannot change any number(1000000000 or 1). Thus the answer is 2. But I test my AC code and some other users' code, the output is 3. My submission ID is 7422755
Why we cant change 1 to 1000000001 ? In description we can change to any integer we want, not neccessarily <= 10^9 (although the constraint of input is between 1 and 10^9). Am i wrong?
Thanks, I did not look into the description carefully and I've got wrong idea.
In problem D, I don't know why you said "So we can solve the problem in O(n^4+a^3log(k)). we should optimize this algorithm." I think the complexity is already O(n^3+a^3log(k)).
DIV 2C(DZY Loves Sequences): should not output of test case 30: 1 2 42 3 4 be 3 instead of 4?
Sequence may be 1 2 42 43 4
I tried to solve 446C - DZY Loves Fibonacci Numbers using sqrt-decomposition technique but got TLE on case 10. Does anbody solved it using this technique ? Or is it solvable using this technique ?
here is my submission 12033435 .
Well, the presenter of these problems is just an eighteen-year old boy from China, hasn't gone to university yet. I know him and I am speechless. TAT -_-|| TAT I can just explain that, the one who almost participates in IOI, but finally dropped out from China Team, has a really really really deep hatred for the world. We are just the victim.
really?
Question about problem Div 2-E
can i solve it with segment tree and lazy propagation ?
if so ... how is the lazy propagation implemented here ??
yes you can, using general Fibonacii sequences starting with a,b as mention in this comment
and this is my implementation 17332378
446B — DZY Loves Modification: maintained two sets for row values and column values. in every iteration 1<=i<=k took the current maximum from row and colum set and picked the greater one. added it to answer and deleted the value from respective set and inserted it after substracting (p* (n or m) ) from it. also maintained two offset variables for row and column as deleting picking one row will effect all column values to decrease by p and vice versa. getting WA. my submision
Did you get any solution for this issue?
I used eigendecomposition for Div1-E. Fortunately there's a sparse set of eigenvectors (with total size $$$O(n \log n)$$$ and eigenvalues are also easy to compute. I wonder why the problemsetters needed to make this problem so brutal, like they purposely wanted $$$O(n \log n)$$$ solutions to fail. $$$m \le 18$$$ would have been challenging enough, without the need for insane constraints and I/O format.
How to implement div2 C using 2 pointers? I implemented it but it was failing on many cases.
Using your solution of Div1A, doesn't this testcase print 2 instead of 3?
The $$$l_i$$$ would be
and the $$$r_i$$$ would be
The only elements that satisfy $$$a_{i - 1} + 1 < a_{i + 1}$$$ are the first and the last if you interpret the element before the first and after the last as $$$-\infty$$$. And for those, $$$l_{i - 1} + 1 + r_{i + 1} = 2$$$ ($$$l_{i - 1} = 0$$$ when $$$i = 1$$$, and $$$r_{i + 1} = 0$$$ when $$$i = n$$$). So the answer is 2. But there is a subsegment of length 3: we could choose the last 3 elements
2 1 3and change the2to a0, and we would have the sequence0 1 3, which is strictly increasing.I know the contest was long time ago, but why is sqrt decomposition method giving TLE in div 1 C. The time limit is given to be 4s and the total number of operations are around 2e8. My code
Just use BS = 700.
Can some one explain solution D with fenwick trees. I have seen plenty of solutions with this code
//fenwick trees t1,t2,t3 //l,r are ranges add(t1,l,f[l]*s); add(t1,r,f[l]*s*(-1)); add(t2,l,f[l+1]*s*(-1)); add(t2,r,f[l+1]*s); add(t3,l,-1); add(t3,r,f[r-l+2]);l--; ll sum1 = get(t1, l)*f[l+4] + get(t2, l)*f[l+3] + get(t3, l); ll sum2 = get(t1, r)*f[r+4] + get(t2, r)*f[r+3] + get(t3, r); ll ans = sum2 - sum1;cout<<(ans+mod)%mod<<endl;
In problem Div1D, the preprocessing task author used to reduce complexity is called matrix inversion.
can anybody help me how to remove MLE in my code link to code thanks in advance!
In problem Div1C, Why can I take the square root in both sides?
$$$383008016^2 \equiv 5 (mod$$$ $$$ 1e9+9) $$$
to
$$$383008016 \equiv \sqrt{5} (mod$$$ $$$ 1e9+9) $$$
There is some modular arithmetic property to do this?
can anyone check the mistake in my solution?
https://codeforces.com/contest/446/submission/92973744
it is a clean code so you won't face difficulty.
if we ignore the time complexity.... the greedy approach at every step gives us the optimal solution or not.
dzy493941464