writer: boleyn.su
O(n):
Let mid = position of ^
Let value(x) = x if x is a digit , 0 otherwise.
Let sum = value(i-th char)*(i-mid)
If sum = 0 then answer = balance
Else if sum<0 then answer = left
Else answer = right
writer: oGhost
O(n^4):
Let f[i][j] = how many money i owes j
#It can be proved we only need to loop n times.
Loop n times do:
For i,j,k in [1..n]
If f[i][j]>0 and f[j][k]>0 then
Let delta = min (f[i][j], f[j][k])
Decrease f[i][j] and f[j][k] by delta
Increase f[i][k] by delta
Answer will be sum{f[i][j]}
O(m+n):
Let owe[i] = 0 for all i
#Suppose there is an agnecy to help people with debts.
#If you owe someone, you give money to the agency.
#If someone owes you, you get money from the agency.
For each ai, bi, ci
Increase owe[ai] by ci
Decrease owe[bi] by ci
Ansewr will be sum{owe[i]|owe[i]>0}
writer: oGhost
O(n):
Because permutation of 1, 6, 8, 9 can form integers that mod 7 equals 0, 1, 2, 3, 4, 5, 6.
So you can construct answer like this: nonzero digits + a permutation of 1, 6, 8, 9 + zeros.
writer: oGhost
O(n*m):
#We can get right[i][j] by O(n*m) dp.
Let right[i][j] = how many continuous 1s is on cell (j, i)'s right.
Let answer = 0
For all column i
Sort right[i] #You can use O(n) sorting algorithm
For j in [1..n]
If right[i][j]*(n-j+1) > answer then answer = right[i][j]*(n-j+1)
375C - Circling Round Treasures
writer: whd
#T = number of treasures, B = number of booms
O(n*m*2^(T+B)):
#State(i, j, ts, bs) means:
# 1. You are at cell (i, j)
# 2. If the i-th bit of ts is 0 i-th treasure cross even edges of current path, otherwise odd edges.
# 3. If the i-th bit of bs is 0 i-th boom cross even edges of current path, otherwise odd edges.
Let dis[i][j][ts][bs] = min step to go to reach state (i, j, ts, bs).
Then we can use bfs algorithm to calculate dis.
The answer will be max{value(ts) — dis[Si][Sj][ts][0]}
writer: whd
O(nlogn) or O(nlog^2n):
Use binary search tree and merge them by rank.
Use binary search tree that supports O(n) merging to get O(nlogn) solution.
O(n*sqrt(n)):
Dfs the tree to transform the problem to:
Given a[i], query [l,r] k.
To solve this problem:
Build sqrt(n) bucket, put query [l,r] into (l/sqrt(n)+1)-th bucket
For each bucket
For thoese queries whose r is also in the bucket (l/sqrt(n) equals r/sqrt(n)), a brute-froce O(n) solution exists.
For thoes queries whose r is not in the same bucket, let we sort them by l. We will get l[i[1]]<=l[i[2]]<=..<=l[i[k]]<=r[i[k]]<=r[i[k-1]]<=..<=r[i[1]](do not forget we get l[] and r[] by dfs the tree!). Solving them can be done in O(n) too.
Since we only have O(sqrt(n)) buckets, the total time is O(n*sqrt(n)).
writer: boleyn.su
This problem can be solved by integer programming:
min sum{c[i]*x[i]}
subject to
sum{A[i][j]*x[j]} >= 1 for all i
sum{x[i]} = R
x[i] = 0 or 1 for all i
where
c[i] = 1 if node i is black, 0 otherwise
A[i][j] = 1 if distance between i and j is no greater than X, 0 otherwise
R = number of red nodes.
As it is known, integer programming is NP-hard.
Thus, this cannot be the solution.
But we can prove the following linear programing's solution is same as the integer programming's.
min sum{c[i]*x[i]}
subject to
sum{A[i][j]*x[j]} >= 1 for all i
sum{x[i]} <= R
x[i] >= 0 for all i
where
c[i] = 1 if node i is black, 0 otherwise
A[i][j] = 1 if distance between i and j is no greater than X, 0 otherwise
R = number of red nodes.
And the known fastest algorithm to solve linear programming is O(n^3.5).
But in fact due to the property of this problem, using simplex algorithm to solve linear programming is even faster. I think it can be O(n^3), but I have no proof.
So just use simplex to solve the linear programming problem above.
The tutorial is not finished yet. More details will be added later.
UPD
Thanks to Codeforces users, a lot of details supposed to be added can be found in comments. I am adding something that is not clearly explained in the comments or something that I want to share with you.
Div1C:
There are few questions about this one. So I am explaining it more clearly.
#State(i, j, ts, bs) means:
# 1. You are at cell (i, j)
# 2. If the i-th bit of ts is 0 i-th treasure cross even edges of current path, otherwise odd edges.
# 3. If the i-th bit of bs is 0 i-th boom cross even edges of current path, otherwise odd edges.
Let dis[i][j][ts][bs] = min step to go to reach state (i, j, ts, bs).
Then we can use bfs algorithm to calculate dis.
About the bfs algorithm:
We know dis[Si][Sj][0][0] = 0.
For state(i, j, bs, ts) we can goto cell (i-1, j), (i+1, j), (i, j-1) and (i, j+1). Of course, we cannot go out of the map or go into a trap. So suppose we go from cell (i, j) to cell (ni, nj) and the new state is (ni, nj, nts, nbs). We can see if a treasure is crossing through the edge (i, j) - (ni, nj), if i-th treasure is, then the i-th bit of nts will be 1 xor i-th bit of ts, otherwise, the i-th bit of nts and ts will be same. The same for nbs.
We can reach state (ni, nj, nts, nbs) from (i, j, ts, bs) in one step, so we just need to start bfs from state(Si, Sj, 0, 0) to get the min dis of all state.
The answer will be max{value(ts) — dis[Si][Sj][ts][0]}
My submission: 5550863
Div1D:
To our surprise, there seems to be many different solutions to Div1D, which is very good. In fact, we thought about changing this problem so that only online algorithm will be accepted, but we didn't have much time to change it. I guess if we only accept online algorithm, the problem will be less interesting becasue we might not have so many different solutions. So, not changing it is a good decision.
However, it may(some solution is hard to change to solve the online-version, so I use 'may') be quite simple to solve the online-version of this problem if you have solved the offline-version. You just need to use persistent data structure when implementing binary search trees. You can get more detail from wiki.
Div1E:
The meaning of the integer programming:
We use x[i] to stand whether node i is red or not. So we have:
x[i] = 0 or 1 for all i
There is a beautiful tree, for each node, exists an red node whose distance to this node is no more than X. So we have:
sum{A[i][j]*x[j]} >= 1 for all i
There are only R red node. So we have:
sum{x[i]} = R
And we need to minimize the swap number, and in fact the swap number equals to number of nodes that changed from black to red. So we need to minimize:
sum{c[i]*x[i]}
After changing it to linear programming:
Firstly, it is obvious that the solution of the linear programming will not be worse than integer programming, because integer programming has stronger constraint.
So we only need to show the solution of the linear programming will not be better than integer programming.
To prove this, we need to show for an optimal solution, there will be an solution which is as good as it and all x[i] is either 0 or 1.
1. Because for "sum{A[i][j]*x[j]} >= 1 for all i", there is no need to make some x[i] > 1. It is obvious that if the solution has some x[i] > 1, we can increase x[i] for nodes that are red in the first place, so that there will not be any x[i] > 1 and this solution is as good as the old one.
2. We need to prove in an optimal solution, making some x[i] not being an integer will not get btter solution. It is really hard to decribe it. So just leave you a hint: use the property of trees to prove and consider leaves of the tree.
My submission: 5523033
There is a nice DP solution too, check this submission 5516578 by Touma_Kazusa.











If the i-th bit of bs is 0 i-th boom cross even edges of current path, otherwise even edges.
In the end "otherwise odd edges"?
Fixed. Thank you.
Edit: Nevermind. Just saw the improved solution later.
Can anyone explain author's Div1 B solution?
My solution (5511286) is also O(NM), but uses no sorting or dp at all.
so am i..but i get wa~
for (int j = 1; j < m; j++) ps[i][j] += ps[i][j — 1];
Is not this dynamic programming? :)
This is just calculation of prefix sums, rather common thing. To some extent it can be called dp, but as you can see there's no dp in the global idea of the solution.
I am not able to understand how to solve "375A — Divisible by Seven". I am still a beginner, so please someone explain the solution in more detail. I've seen that it is mentioned "The tutorial is not finished yet. More details will be added later" in the end of the tutorial. So, if it is not regarding this question, please include the solution to this question also. Thanks.
http://codeforces.com/contest/376/submission/5509530 you can see the solution i have submitted with this logic.
+1! i understood the solution. Thanks.
rforritz How did you make the DP[] array?? What was the logic behind it ??
I don't know how he did, but I used a calculator to find them out and it only took less than 5 mins. After all there are only 4! = 24 possibilities.
How about following
See this code.
rforritz Could u please explain your dp array please.I am not getting reason behind printing out dp[rem] after printing non zero digits.
But why are you doing rem = rem*10+i. ?? This is really mysterious
In problem 375B (Maximum Submatrix 2), won't sorting right[i] require O(m) time (using counting sort), since the values of right[i] may vary from 0 to m? That'd change the overall complexity of the algorithm described to O(m*(m+n)).
pretty much the same complexity anyway.
Yeah. That's true. I was (and still am) just trying to determine whether my understanding of the given solution is correct.
In the explanation of Div1 D this makes no sense to me:
l[i[1]]<=l[i[2]]<=..<=l[i[k]]<=r[i[k]]<=r[i[k-1]]<=..<=r[i[1]]
How do we know that r[i[k]]<=r[i[k-1]] ?? We sorted by l, so what if 2 queries overlap? This seems to be saying that all queries are nested.
do not forget we get l[] and r[] by dfs the tree!
what is l[i[k]]?? i don't understand the O(nsqrt(n)) soloution!
do you have an implementation? tnx
I think, that
i[1], i[2], ..., i[k]is a permutation of queries in one bucket after sorting them byl.Because we get
l[]andr[]bydfs()they can not overlap.And because every
r[i[j]]in other bucket, finally we getl[i[1]] <= l[i[2]] <= ....You can look at my submission, it a bit differs from editorial, but maybe it will help.
tnx for your answer i think i get it now but how does queries not overlapping improve the time complexity?? i think your submission is O(nsqrt(n)) even if queries could overlap, am i wrong?
Yes, my submission always works O(n·sqrt(n)), but if we iterate buckets, sort queries in each bucket and brute force all small (lenght < sqrt(n)) queries, after it, we can just expand our segment from smallest to largest in bucket, this implementation can be easier (just call
add(l[i + 1], ..., l[i] - 1)andadd(r[i] + 1, ..., r[i + 1])).thanks for sharing this! I am stucked at the point of calculating suffix sum(i have done it using segment tree) but your solution provide me the way! Thanks :)
We can get a simpler O(nlogn) solution for problem D by combining rng_58 / crx's solution and bakabakashyoshyo's solution.
Implementation:5516493
Can somebody explain why rng_58's solution works? I can't understand why executing clear_all and add_all for each child except the one with maximum subtree in the dfs of each vertex works in time?
We can focus on the number of "clears", that is, how many times each node is cleared.
Let size[u] be the size of subtree u. Suppose we are performing "dfs(u)" and w is a son of u, v is in the subtree of w. Then, if v is cleared in "dfs(u)", size[u] will be at least 2*size[w]. That is, every time v is cleared, the size of the subtree v belongs to will double. So each node v will be cleared at most O(logn) times and "clear" operation will be performed at most O(nlogn) times totally
And for each node, the number of "add"s = the number of "clear"s + 1, so "add" operation will also be performed at most O(nlogn) times.
"if v is cleared in "dfs(u)", size[u] will be at least 2*size[w]", It's reasonable in binary tree. Is it still true for trees with more than 2 forks? Since, the tree in the problem is not necessarily binary. What I am thinking of, if u have k subtrees, at most (k-1)/k * size(u) vertices will be cleared. That is each "clear" will increase the tree size to at least k/(k-1) the size of the subtree. when k=2, it will at least double the tree size.
let b be the largest son of u, it's obvious that size[b] >= size[w], then size[u] > size[b] + size[w] >= 2*size[w].
Note that here size[w] isn't the size of all the subtrees other than b, it's just the size of the subtree that node v currently belongs to.
I have the same doubt, on each step we clear all but the largest subtree. Does this imply the complexity is O((n + q) × lg(n))? Can someone explain.
For question "Divisible by Seven" IN the question it says
But solution says So you can construct answer like this: nonzero digits + a permutation of 1, 6, 8, 9 + zeros.
So which one is correct?Can someone explain it more clearly?
both are correct. Because it is mentioned in the question that It is guaranteed that the record of number a contains digits: 1, 6, 8, 9. Number a doesn't contain any leading zeroes. The decimal representation of number a contains at least 4 and at most 106 characters. The decimal representation of number a contains at least 4 characters and they are 1,6,8,9. Now according to the answer So you can construct answer like this: nonzero digits + a permutation of 1, 6, 8, 9 + zeros. even if nonzero digits are null a permutation of 1, 6, 8, 9 will be there and hence the answer will not contain leading zeroes. I think you also missed the point that a will at least contain 4 characters like me. So, you felt there is some ambiguity
Ok..i try to rephrase the solution in my own words like this. from the number given,i take all the non zero numbers and put them at the start.take try all permutation of 1689 which , when put at the end of the given starting part ,produces 0 mod 7.Then add remaining zeroes
All non zero digits+some permutation of 1689 such that the number(as a whole) produces 0 mod 7+ remaining zeroes.
is that correct?
Actually, i was also not able to understand the solution till i asked in comments and rforittz commented. I think you will understand better after seeing his solution, http://codeforces.com/contest/376/submission/5509530.
I used the O(m+n) method to solve Problem 376B, but got WA.
I saw accepted solutions of others where they added the abs() of the -ve values in the array and then divided the total by 2, but I didn't understand the logic behind it.
Please help!
Because abs (sum of all negative numbers in the array) = abs (sum of all positive numbers in the array)
for problem B Div2: My accepted solution gives output as 290 for this testcase
shouldn't the answer be 310?
for ur case if we do like this a[1]-=10,a[2]+=10; a[2]-=30,a[3]+=30; a[3]-=300,a[1]+=300; so final values are a[1]=290,a[2]=-20,a[3]=-270; here u see only a[1] is positive , meaning that it is the only value of dept that is valid in the system,negative values just mean that the corresponding people have to pay the dept , but only the positive values are going to decide the total dept to be paid after deleting the cycles...
no 290 is correct
Please Someone Clarify the idea of Div-1 A ( also Div-2 C) Divisible by Seven
And in this solution how DP[] array was made?
Suppose you have a number with x digits, since the problem says the number contains digits 1,6,8,9 we can remove these digits from the initial number... Let's imagine the number with the four digits removed is y. After getting y%7 we can have 7 possible values ,[0..6].
We want a number divisible by 7, so we want the entire number to be 0 modulo 7. So, for each possible value of y%7, we have to get one permutation of 1689 so that this permutation modulo 7 + y%7 = 0 (mod 7).
If you get the value modulo 7 of all the permutations of 1689, you'll notice that all of the seven values,[0..6], are possible. Therefore, there will always be a permutation so that y concatenated with it will end up on 0 modulo 7.
About the question: Probably the writer of this solution generated all of the 24 permutations and chose seven of them, each one giving a different value mod 7.
Thanks dcms2 for helping me big time understanding the solution :)
I can't understand the following part in DivI C:
Can anyone help me?
Well, how I see the solution more detailed:
First of all, let's fix the direction of the ray for each object, that will not pass through any other point on the grid. For example, the ray that comes by the vector (42, 43).
Then we do the following. Let's fix the state consisting of (i, j, treasures_mask, bombs_mask), where (i, j) is our current position, treasures_mask is the mask, where for each treasure it's bit is equal to the its ray crossing number oddity, and bombs_mask is the same for bombs. This state fully describes, what profit of collecting treasures we are going to get, if we have such state at the end of our journey (i. e. finally we need to return to the state (start_i, start_j, as_big_as_possible_mask_of_treasures, 00...00)).
From all ways to reach such state, we need to select the one that minimizes length of the path. So we can reduce our problem to the minimal-distance problem on unweighted graph of states. That can be done using BFS — the answer is maximal (cost(mask_of_treasures) - distance(the_state_that_gives_us_such_mask)) value between all possible terminal states.
UPD: Here is my code that implements exactly what I described (the only difference is that I merged two masks for bombs and treasures into one): 5518676
Nice, thanks.
In the div2 B task, why we need to increase a[i][k] by delta as author indicated? It seems to me I don't get idea, could anyone explain me author's solution.
you can use the second approach. which is much easier and faster.you can think like this way- for each person how much of his money is in the field. this value is the difference between the money he owes and the money other people owes him. if the value is positive then he has money in the field, sum it up with the final answer.
Here is my solution 5505331 hope this will help you
A owes B delta+x, B owes C delta+y, A owes C z
is equal to A owes B x, B owes C y, A owes z+delta
and you can see, the total is decreased by delta (delta+x+delta+y+z-x-y-z-delta=delta).
I finally found time to properly code my idea for Div1 D in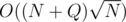 . It uses a lot of simple concepts in tree programming:
. It uses a lot of simple concepts in tree programming:
split the colours into heavy (frequent, occurences) and light (rare,
occurences) and light (rare, 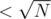 occurences) ones; calculate all the answers for light colours and queries with
occurences) ones; calculate all the answers for light colours and queries with 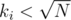 , and for every query, iterate over heavy colours and check how many times they appear in the subtree
, and for every query, iterate over heavy colours and check how many times they appear in the subtree
convert subtrees into intervals by pre-order DFS — vertex i gets an interval I[i] = [I[i].x, I[i].y); for every heavy colour c, build an array of prefix sums of array A, where A[I[i].x] = 1 if the colour of i is c and A[I[i].x] = 0 otherwise; the number of occurences of colour c in subtree of i is the sum of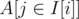 , which can be obtained from the prefix sums in O(1)
, which can be obtained from the prefix sums in O(1)
for light colours, we'll build another array B[j][i]: how many light colours appear exactly j times in the subtree of i, for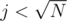 , and then convert it to prefix sums (not "exactly j", but "at most j") in-place
, and then convert it to prefix sums (not "exactly j", but "at most j") in-place
How to build B? Firstly, we can iterate over all light colours, over all vertices of the given colour, and put 1 in a BIT for every vertex of that colour (BIT[I[i].x] = 1 for vertex i); then we can count occurences of that colour in any subtree (interval I) in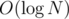 . Now, imagine that we're just doing a bruteforce solution: for every vertex i of the tree, we ask the BIT how many (a) colours there are in its subtree, and increment B[a][i].
. Now, imagine that we're just doing a bruteforce solution: for every vertex i of the tree, we ask the BIT how many (a) colours there are in its subtree, and increment B[a][i].
We can do this more efficiently by noting that if there are k vertices of colour c, then there are just O(k) vertices for which the a we get is different from the one we get for that vertex's parent. If we knew the lowest ancestor j of i for which a is different, we could just decrement B[a][j], increment B[a][i] and after doing that for all colours and all vertices where it's required, we could process the vertices i in reverse order of BFS from the root and keep adding B[j][i] to B[j][parent[i]], after which we end up with the same array B. Also note that we only need to do this for vertices where a changes — e.g. for all those of colour c and those which we note in this algorithm as lowest ancestors with different a; that can be done efficiently as long as we process them in reverse BFS order.
We also need to know how to quickly get the lowest ancestor with different a. We can use an LCA preprocessing table for that — it tells us the 2k-th ancestor of every vertex. We can try to get to the highest ancestor of i from that table with the same a by trying the highest possible k, decreasing k if that ancestor has different a and moving to the ancestor otherwise; note that after successfully moving to the ancestor, we don't have to consider higher k again, because if that was successful, it'd be successful before the jump as well, which is impossible. Checking a takes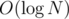 time and possible k go up to
time and possible k go up to  , so the time required for that is
, so the time required for that is 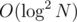 per vertex. (Beware of the case where no ancestor with different a exists.)
per vertex. (Beware of the case where no ancestor with different a exists.)
Since every vertex has just 1 colour, we only do the above O(N) times total, so this part of the algorithm takes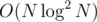 time. Then there's
time. Then there's 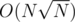 completing of arrays A and B to prefix sums and
completing of arrays A and B to prefix sums and 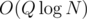 time for checking the prefix sums of A for every query; from prefix sums of B, we can get the part of the answer over all light colours in O(1).
time for checking the prefix sums of A for every query; from prefix sums of B, we can get the part of the answer over all light colours in O(1).
Code: 5520580
I had the same thought during the contest but could only come up with a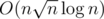 implementation for building B... Your idea brightens me a lot!
implementation for building B... Your idea brightens me a lot!
we can also use Mo s algorithim to solve this question by modifying the euler tour of the tree,and then problem is just not calculate number of values in [l,r] that have frequency >=k
I don't know if anyone is interested in knowing that, but I can hack my own solution to A :P. I chose first positions of 1, 6, 8, 9 and iterated over all their permutations and if that failed, I was iterating over all permutations of input until I found a solution — first phase was my first idea and I added second phase "for safety reasons" :D. This is an example of input which causes my code to gives TLE. 10000060000080000090000000000000000000077777777777777 And here is my code: http://codeforces.com/contest/375/submission/5503504 Swapping 1, 6, 8, 9 won't change residue of this number in dividing by 7 and so changing this number by next_permutation (for a large number of iterations) :P.
can someone plz give a detailed explanation for div 2 problem 4 ,,cant figure out the logic of the tutorial..thnx
A submatrix composed of some subrows, all of them starting and ending in the same column.
We'll pre-calculate one useful array: A[i][j] is the maximum number of consecutive 1-s to the right of cell (i, j), including (i, j). That can be counted by simple DP: for (i, j) containing a 0, A[i][j] = 0 and for (i, j) containing a 1, A[i][j] = A[i][j + 1] + 1, because we can take all consecutive 1-s to the right of cell (i, j + 1).
Imagine we chose that starting and ending column (l and r). To get the largest answer, we need to count how many subrows with that starting and ending column are composed of just 1-s. That's the same as counting all i for which A[i][l] ≥ r - l + 1.
We need to do this efficiently. We can iterate over all l, but not over all r. Still, if we listed and sorted all A[i][l] for given l, then we don't need to consider all r, just all A[i][l] and for the k-th largest of them, there are N - k + 1 larger/equal A[i][l]s. The sorting can be done in linear time (CountSort) and we only need to traverse the sorted array once for every l.
thnx @Xellos for such a nice explanation..
Can someone please explain how to solve Div1 D with treap? I saw some solutions with treap, but I don't unterstand it.
In Div1 B, I get TLE if I read the input using
cin(here), but get AC if I read it usingscanf(here). Reading isO(MN), so it should run fine, givenM, N <= 5000. I prefer usingcin. Why is it slower in this case and when should I watch out?Reading 25 million numbers can TLE if you're using slow i/o methods (cin without sync_with_stdio(), scanf on individual characters etc.).
Thanks. Tried using cin on individual characters with sync_with_stdio() and worked (5530346).
Can anyone explain me the logic behind the solution for 375B?
OH god, just find out the error in my thinking!
In Div 1 C , how can we pass from one state to another state in BFS ? Can somebody explain this or I must analyse codes ? Authors should write more detailed tutorial .
It's like a BFS on a graph. If you just wanted to find the shortest path from the start to cell (i, j), you'd use a BFS on the graph whose nodes are cells and edges go between adjacent cells. This time, you add one more information to nodes' decription: a bitmask saying which treasures/bombs are "inside" the path drawn so far, by the definition from the problem statement; the edges still go between adjacent free cells and have uniform cost.
That BFS just tells you the shortest path in which you include some subset of treasures and bombs; you can iterate over all subsets of treasures and choose the one that maximizes the total gain.
Thank you very much . I have one more question . Why BFS works and DFS doesn't work? When we add another information , which changes the distance between vertices , why BFS will still work ?
? In this graph you got (number of fields) * 2^(number of treasures and bombs) vertices, I don't understand, what do you mean by "changing distance between vertices". (i, j, 1, 0) is completely different vertex from (i, j, 0, 0).
PRO D div 1 "For thoes queries whose r is not in the same bucket, let we sort them by l. We will get l[i[1]]<=l[i[2]]<=..<=l[i[k]]<=r[i[k]]<=r[i[k-1]]<=..<=r[i[1]](do not forget we get l[] and r[] by dfs the tree!). Solving them can be done in O(n) too."Can anybody tell me how to solve it in O(n)?
Oh I see...
Can someone please explain me solution to Division 2,Problem D. It is said that the rows can be rearranged. In my understanding it is something like : Row 1 and row3 can be interchanged. but by sorting the matrix how does we achieve that.
Can someone please explain that.
Let input matrix is
now when you are at column 1 make a array ca with the values of column 1 of Consecutive sum from right matrix for column 1 ca = [0,2,2,0] . for column 5 ca will be [2,2,0,2] ( I hope you get the idea )
Now follow this algo
Now try to think why we are making ca and sorting ca instead of sorting the whole matrix :)
The submission you linked as a DP solution of Div1E is a submission of Acme to Div1C :P.
fixed, thank you.
Can anyone explain me the tutorial of Div1 D, that says: "For thoes queries whose r is not in the same bucket, let we sort them by l. We will get l[i[1]]<=l[i[2]]<=..<=l[i[k]]<=r[i[k]]<=r[i[k-1]]<=..<=r[i[1]](do not forget we get l[] and r[] by dfs the tree!). Solving them can be done in O(n) too." How to solve it in O(n) time?
you calculate l[i[k]] to r[i[k]] first and then l[i[k-1]] to r[i[k-1]] and then l[i[k-2]] to l[i[k-2]] and so on.
Oh, I understood! Thanks a lot!
i am having problem with div 2 ques d .. i understand the authors solution but all AC solution give 4 as ans for this test case: 4 3 100 011 000 111
ans = 4
Should'nt 3 be the ans ? are we allowed to move rows together or we are not looking contiguous rows and columns ? Can any one please explain me the ques if my understanding of ques is wrong
4 3 100 011 000 111
best answer is to swap 3rd and 4th row: 100 011 111 000 then (2,2) to (3,3) is 2*2=4.
so it means row swap was allowed ? I did'nt see it mentioned anywhere in the problem statement .. are column swaps also allowed ?
Even if you didn't see it, it was there. Right in the first line.
You are allowed to rearrange its rows.Rearrange = swap all you want.
There's nothing mentioned about columns, so you can't swap columns.
DIV1E is similar to this problem : http://acm.hdu.edu.cn/showproblem.php?pid=4735
What is the O(n) sorting algorithm in the solution for 375B — Maximum Submatrix ?
use the counting sort
I didn't know this algorithm. This is very cool! Thanks!
i was about to code div1 D with nlogN . just saw author's complexity, way awesome idea with easy implementation
Can anyone explain the O(N logN )solution of DIV1 D. It is not explained properly in editorial . How to use Binary search tree in this question. Thanks in advance :)
In div1 E, I am unable to prove that any optimal linear programming solution can be converted to an integer solution. Can someone help?
There's an alternative solution to problem $$$D$$$, which I believe runs in $$$\mathcal{O} \left( N (\log_2 n)^2 \right)$$$. I'm not entirely sure of name of the technique: it's somewhat similar to small to large merging; I've heard the word 'sack' or 'dsu on trees' to describe it.
I'll start with the (slow) small-large merging idea. For each subtree of each node, we document three things:
The number of occurrences of each color.
The set of colors with a given number of occurrences.
A segment tree on the size of the set of colors of a given number of occurences. Think of this is a segment tree on an array which tells us how many colors appear $$$i$$$ times.
Merging is now quite simple: simply update (1), (2), and (3) straightforwardly. To process queries, when we're at a subtree, answer queries of that subtree (offline).
However, this will probably TLE because maintaining a segment tree of size up to $$$10^5$$$ at each node is unneeded. To fix this, we can do basically the same thing, except the 'sack'/'dsu on tree' version. In short, we need to be able to merge and remove subtrees, and we merge the smaller subtrees into the global smaller one, and remove some of them if needed.
153192706
question is why the problem author of 'Lever' expected that everyone will know physics ?