Introduction
I have no school right now, and there's no tutorials on Tree Isomorphism on Codeforces, so I decided to write one :).
What is a tree isomorphism?
Maybe you recognize the word isomorphic: in the context of abstract algebra when two objects are effectively the same, but are labelled differently. We can extend this to trees as well: two trees are isomorphic if they are the same, but may have different node labels. For example,
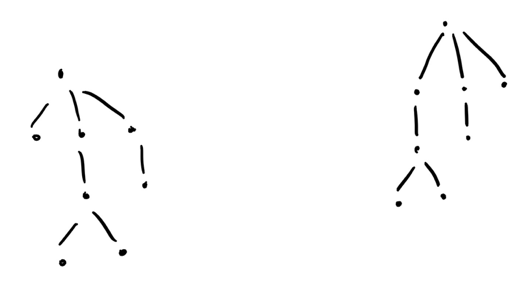 are isomorphic because we can relabel the nodes. If you want a more rigorous definition, then two trees $$$T_1 = (V_1, E_1)$$$ and $$$T_2 = (V_2, E_2)$$$ are isomorphic iff there exists a $$$\phi$$$ for which $$$\phi(E_1) = E_2$$$ and a $$$\phi^{-1}$$$ for which $$$\phi^{-1} (E_2) = E_1$$$.
are isomorphic because we can relabel the nodes. If you want a more rigorous definition, then two trees $$$T_1 = (V_1, E_1)$$$ and $$$T_2 = (V_2, E_2)$$$ are isomorphic iff there exists a $$$\phi$$$ for which $$$\phi(E_1) = E_2$$$ and a $$$\phi^{-1}$$$ for which $$$\phi^{-1} (E_2) = E_1$$$.
What is the problem?
We want to determine if two unrooted trees are isomorphic in $$$\mathcal{O}(N \log N)$$$ time.
If we can solve the problem for rooted trees, can we solve it for unrooted trees?
Yes. We can transform our original problem of checking if two trees are isomorphic into checking if two rooted trees are isomorphic easily. How? We can find the centroids of our first tree and our centroids of our second tree, and then root them at their centroids. So now, we have transformed our unrooted case into a rooted case.
Heuristics
You can skip this, if you'd like. I'm just going to list out some ideas for tree isomorphism checking. All of the following ideas won't solve the problem, but some of them work decently well.
Idea 1: Find the degrees of all nodes and check if $$$\text{oc}_{T1}[i] = \text{oc}_{T2}[i]$$$, where $$$\text{oc}_{T}[i]$$$ is the number of vertices of degree $$$i$$$. If $$$\text{oc}_{T1}[i] = \text{oc}_{T2}[i] \forall i$$$ does not hold, then we know that the trees are not isomorphic.
Idea 2: Root the trees at their centroids. $$$\text{oc}_{T1}[i] = \text{oc}_{T2}[i]$$$, where $$$\text{oc}_{T}[i]$$$ is the number of vertices with subtree size $$$i$$$. If $$$\text{oc}_{T1}[i] = \text{oc}_{T2}[i] \forall i$$$ does not hold, then we know that the trees are not isomorphic.
Idea 3: If the diameters of the tree are not the same, then they cannot be isomorphic.
Idea 4: We know that for fixed $$$k$$$, the number of paths of length $$$k$$$ must be the same in both trees.
If we merge all of the ideas together, we will get a pretty good heuristic and will be able to identify with pretty good accuracy if a tree is isomorphic to another tree. But that's not good enough.
The idea
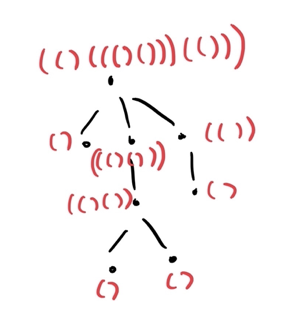
The idea is to parenthesize our tree. We can recursively, say that:
where $$$+$$$ denotes string concatenation. But obviously, the string parenthesization for rooted trees do not always yield the same result, even for isomorphic trees:

So what can we do? It turns out, we can just "order" the parenthesization. That is, concactenate in increasing or decreasing order of the string parenthesization.
How would it look like if we did that?
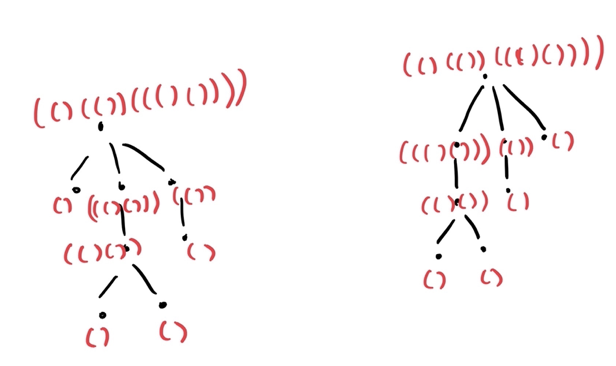
So, in short, the idea is to parenthesize the tree and then concactenate in some fixed order (one easy way is in increasing order of the strings).
But that's $$$\mathcal{O}(N^2)$$$, since we're dealing with a lot of potentially large strings. No problem! We can replace each opening parenthesis with a $$$1$$$ and each closing parenthesis with a 0. For example, $$$(()())$$$ would become $$$110100$$$. We can then convert the binary string to a number, by using it's binary representation. In the case that the number is too large, we can take it modulo some large prime $$$p$$$.
The end.










There is a way to avoid using hashing too. Compress the corresponding parentheses strings into unique integers, and check for each level separately. Note that there can be a total of $$$O(n)$$$ unique integers, so if you use radix sort, you can do this in $$$O(n)$$$. This is a good reference imo.
Edit: This is an implementation of this idea, hopefully it's clearer now.
Interesting!
norz
You don't need a notion of bracket sequences to check rooted trees for isomorphism.
You can do it like this — let's assign each rooted tree a unique number. Knowing the assigned number for a rooted tree is the same as knowing a multiset of assigned numbers of the subtrees of its root children.
If we've already seen the multiset before, we extract its number from a map, otherwise we assign it the first unassigned number. It is implemented like this:
It is $$$O(n \log n)$$$ rather than $$$n$$$, but I guess the radix sort idea above could still apply?
Another problem to test rooted tree isomorphism algorithms: 102354J - Tree Automorphisms.
P. S. If you don't sort vector
xinhashify, you'll still get a meaningful compression — with this approach you get to check if two rooted trees are isomorphic as plane trees.My implementation in particular doesn't use any bracket sequence (rather, it only relies on the fact that for a given level, we assign each unique subtree with root at that level a unique integer; uniqueness of subtrees is defined up to isomorphism). My initial idea was similar to yours: map each vector to a unique integer; however, it is more efficient to only care about the current level and do a radix-sort style compression for assigning vertex representations to the current level.
[deleted comment]
There is a mistake in the 3rd Right sided Image, you forgot to count one node . BTW Nice Editorial , and thanks I didnt knew anything about this.
This tree isomorphism problem appeared in Latin America ICPC Regionals a week ago. I am the author of it, I thought this post would help many teams to solve it, but sadly no ACs during contest. The problem is not as straight forward as checking if 2 trees are isomorphic though.
The problem is pretty straightforward, it's just a huge implementation problem in a contest with too many problems.