Good morning Codeforces!
Today's post regards a well-known, but surprisingly hard to learn topic, Euler Tour Trees.
Prerequisites:
- Basic tree knowledge, e.g. general vocabulary
- Balanced Binary Search Tree Knowledge (e.g Treaps/Splay trees). In my opinion, learning treaps is the easiest, and SecondThread has a great video/problemset on treaps, so go check it out here! The BBST must store parent pointers, so make sure your implementation supports it.
Disclaimer
This idea will definitely not show up in easy problems, and is pretty uncommon. Nevertheless, it's a cool concept and it can be used to “cheese” somewhat difficult problems, and I haven't found any resources that describe it well.
Brief Description of Operations
A Euler Tour Tree is a representation of a dynamic forest of trees. This means that, as long as the graph never contains any cycles, you can support the following operations in $$$\mathcal{O}(\log{} n)$$$ per operation:
- Adding an edge to the forest
- Removing an edge from the forest
In addition, you can perform various operations like:
- Rerooting a tree
- Check if two nodes are connected
- Modifying an entire subtree (e.g. increasing every node in a subtree by some number)
- Query some subtree aggregate (e.g. finding the sum of a subtree)
Definition of an Euler Tour:
The Euler Tour of a tree is defined in various ways, depending on the source. However, I've found that one specific way is generally better in this context. The idea is to store the tree as a list of directed edges in a DFS order.
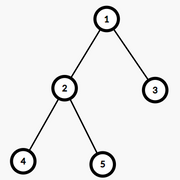
For example, the Euler Tour of this tree would be $$$[(1, 2), (2, 4), (4, 2), (2, 5), (5, 2), (2, 1), (1, 3), (3, 1)]$$$. This is because, while doing a DFS on this tree, you would start off by going from node $$$1$$$ to node $$$2$$$, from node $$$2$$$ to node $$$4$$$, from node $$$4$$$ back to node $$$2$$$, etc.
General Structure
The main idea of Euler Tour Trees is to store the Euler Tour of the tree (hence the name) in some kind of balanced binary search tree (BBST). The split/merge operations offered by BBST's will prove to be extremely useful while implementing the add edge and delete edge operations.
There are a couple of helpful properties in an Euler Tour that we will need:
- Every edge is stored exactly twice, once for each direction. This implies that there are $$$2(n-1)$$$ edges in a tour.
- Any cyclic shift of the Euler Tour is still an Euler Tour, but with a different root. This is because the tour is effectively a cycle, and starting a cycle from anywhere is still a cycle.
However, there is one issue that arises: a tree of size $$$1$$$ has an Euler Tour of size $$$0$$$. This is especially an issue when we're using Euler Tour trees, and we're representing a forest of trees (so a degenerate case is very possible). To deal with this, we'll add an extra self-loop $$$(c, c)$$$, for every node $$$c$$$, in the Euler Tour such that the loop occurs right after we enter its corresponding node. This provides a way to support storing values on the nodes as well, not just the edges, when calculating our aggregate operations.
The Operations
Here I'll describe how each of the different operations we're trying to support change the Euler Tour, and how we can reflect those changes in our data structure.
Important note: For all future queries, to locate an edge $$$(a, b)$$$ in the BBST's, you can store a map from "edge" to pointer in the BBST.
Reroot
The reroot operation will be used in the implementation of the future operations, so I will describe it first. The function $$$\text{reroot}(c)$$$ does the following: modify the structure so that it represents the Euler Tour such that you start the DFS at the node $$$c$$$. Recall that any cyclic shift of the Euler Tour is still a valid Euler Tour, so all that's required is finding how much to cyclically shift the edges by (the actual cyclic shift operation can be implemented in $$$\mathcal{O}(\log{} n)$$$ with a BBST). The self-loops that we included make this extra convenient; shifting the tour such that the edge $$$(a, a)$$$ is the first in the list will reroot the tree exactly as intended.
Add Edge
There are three steps when adding an edge between $$$(a, b)$$$:
- Call $$$\text{reroot}(a)$$$, so that $$$(a, a)$$$ is the first edge in $$$a$$$'s Euler Tour.
- Perform the “reverse” of $$$\text{reroot}(b)$$$, such that $$$(b, b)$$$ is the last edge in $$$b$$$'s Euler Tour.
- Merge the two BBST's together (with $$$a$$$'s going before $$$b$$$). Make sure to add the edge $$$(a, b)$$$ in between $$$a$$$ and $$$b$$$ and the edge $$$(b, a)$$$ after $$$b$$$.
Remove Edge
There are 3 steps when removing an edge between $$$(a, b)$$$:
- Cyclically shift the edge $$$(a, b)$$$ to the front of the tour.
- Remove the edge $$$(a, b)$$$ (now at the front), from the BBST.
- Locate and remove the edge $$$(b, a)$$$ from the BBST.
After performing these three operations, the tour will be split into two independent parts (both of which are valid tours of the subtrees)
Subtree Aggregates
To maintain subtree aggregates, one must store subtree aggregates of the values on the edges in the BBST. These will easily get updated while performing the add/remove edge operations. The use of self-loops makes storing weights on vertices extremely simple: just store the values on the self-loop.
Weights can also be updated, by just finding and updating the corresponding edge in the BBST.
Connectivity Checking
This query checks if two nodes $$$a$$$ and $$$b$$$ are in the same component. This can be done simply by just checking if the self loops $$$(a, a)$$$ and $$$(b, b)$$$ are present in the same BBST (e.g. checking if the root of the BBST is the same).
Sample Problems
Thanks for reading the blog! Let me know if you have any suggestions about additions/changes to the blog, or additional sample problems.











Worth noting that if relax a bit ability to change tree structure: remove reroot and replace operation add edge to operation change parent of vertex, you can support additional operations: lca and path sum (or simply just distance between two vertices). For this, however, you need to maintain different euler tour: the one that used in LCA via sparse table.
PurpleCrayon please teach me how to be as good as you :orz:
... maybe adding some code to each topics u describe could be more helpful...
It is my first time coding ETT but here is my attempt:
yosupo vertex add submission
yosupo subtree add submission
If you wanted to use treap instead, you exchange splay with treap template, then change get() and ind().
Thanks for the blog!
Is there any use case where euler tour tree might be better than link cut tree (speed, memory usage, ease of implementation, or an operation not supported by link cut tree)?
easier to implement subtree queries (although at that point I just copy my old template)
There are two main reasons I would use it:
Also, ETT's are used for general online dynamic connectivity, but that's (hopefully) unrelated to CP.
Is it possible to never use(or never learn) link cut trees after learning Euler tour tree, similar to Kruskal and Prim?
LCT's can perform operations that ETT can't (e.g. path queries along with all of the dynamic tree operations). The way I think about it is this: LCT's deal with paths, and ETT's deal with subtrees (this isn't strictly correct, since LCT's can maintain subtree info, but it's usually true.
Try solving this with kruskal's :clown:.
It is good to at least have awareness of alternate methods when they exist, as it leads to better understanding and are sometimes necessary.
Am I right that you can't support both subtree aggregate and add/remove arbitrary edges knowing only subtree root and whole tree root vertices (no matter can whole tree root be changed or stay fixed during all operations)? I think, in your sample problems it's possible only because of additional information which edge came from your parent and that seems rather restricted case.
This is just poor man's LCT.