Hello! In the previous post I've introduced two kinds of dynamic programming: Regular and Process Simulation. In it I've told how to solve DP problems using Process Simulation, please read it if you missed in order to understand the difference. Now I want to talk about tricks that help me solve DP problems with Regular approach.
While with the Process Simulation approach we had to invent some process that would build us the desired objects, in the Regular approach we're going to deal with the objects directly. Each state of the DP (i.e., a set of values for each parameter) will correspond to some class of the desired objects, and the corresponding value in the DP table will contain some information about that class, which is in fact equivalent to the Subtask formulation I've introduced in the previous post.
In this post I'll focus on how to come up with transitions for the Regular DP, if you are already decided on the parameters. The general plan is:
Determine, what is a considered object in the problem. Preferably display it visually.
Break the considered objects into classes and try to cover each class with a set of transitions to the lesser subtasks of the problem.
First cover what can be covered in an obvious way, and then focus specifically on what remains.
An Example
informatics.msk.ru: ? and * Template You have two strings called "templates" consisting of Latin letters and signs '*' and '?'. You consider a string to fit the template if it can be obtained from the template by changing every '?' to some letter and every '*' to some string of letters (possibly empty). Find the length of the shortest string that fits both templates.
Again, if you really want, it is possible to solve this problem using Process Simulation, but I think this solution will be quite unnatural. So let's proceed with the Subtask approach, or more precisely the Objects Classification approach.
Let's introduce some parameters to this question. A common way to do it in such problems would be to ask the same question about some two prefixes of the templates. That is, "what is the length of the shortest string that fits both of the templates, but if we only consider the first i symbols of the first and the first j symbols of the second template?". Every state of our DP will correspond to such class of strings and the corresponding value in the DP table will store the length of the shortest of such strings.
Now suppose we find the answer for each such question in such order that when we are handling the state dp[i][j], we already know the answer for all smaller pairs of prefixes (we know all the dp[i'][j'], where i' <= i and j' <= j except for the dp[i][j] itself). How can this knowledge help us find the value for the current state? The answer is, we need to look at the current group of objects and to further split it into types. Let's consider three cases:
If none of the prefixes' last symbols is a '*'. Then, obviously, the last symbol of the answer string shall correspond to both of those symbols. Which means, if they are two different letters then the set of answers is empty (in which case we store inf as the shortest answer's length). Otherwise, without its last symbol, the answer string shall fit for the prefix of length i - 1 of the first template and the prefix of length j - 1 of the second template. Which means there is a one-to-one correspondence between the set of answers for the state dp[i][j] and the set of answers for the state dp[i - 1][j - 1]. And the shortest answer for dp[i][j] is larger than the answer for dp[i - 1][j - 1] by one, i.e. dp[i][j] = dp[i - 1][j - 1] + 1.
If both of the prefixes' last symbols are '*'. Then we can see that among all the answers the shortest one will be such that at least one of the two '*' corresponds to an empty string within it (because otherwise we can throw away some of the last letters of the answer and make it shorter, while still valid). Thus, we can split the answers/objects, corresponding to the state dp[i][j] in three groups: the ones where the '*' of the first template's prefix is changed to an empty string, the ones where the '*' of the second template's prefix is changed to an empty string, and the ones that are surely not the shortest. We know the shortest answer in the first group (dp[i - 1][j]), we know the shortest answer in the second group (dp[i][j - 1]) and we don't care about the third group. Thus, in this case dp[i][j] = min(dp[i - 1][j], dp[i][j - 1]).
Note: attentive readers may have noticed that what we consider an object in this problem is actually not just a string corresponding to two templates, but a combination of such a string and such correspondence (i.e., to which characters exactly are the '*' changed to form that string).
If only one of the prefixes' last symbols is a '*'. This is the most interesting case, where it is not obvious how can we know the answer given the answer for smaller subtasks. In such cases I recommend to forget about the rest and just ask yourself anew, what are the objects that we are looking for? Let's say that the first template's prefix is s[0]s[1]...s[i - 1], s[i - 1] = '*' and the second template's prefix ist[0]t[1]...t[j - 1], t[j - 1] != '*'. In this case we specifically want to find a string a[0]a[1]...a[n - 1] such that a[n - 1] is equal to t[j - 1] (or to any letter if t[j - 1] = '?') and a[0]a[1]...a[n - 2] fits the second template's prefix of length j - 1, and on the other hand with some prefix – possibly the whole string – fitting to the first template's prefix of length i - 1.
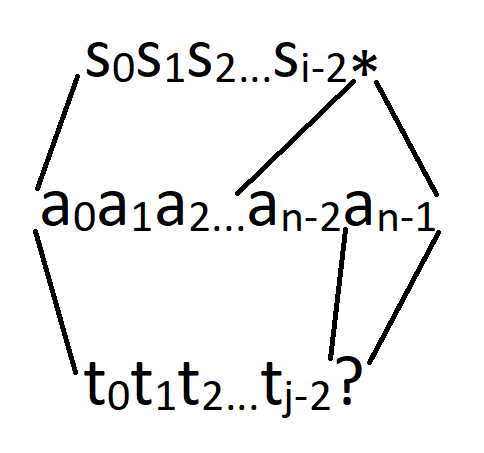
First take care of the obvious
The first part of the statement is good: "a[0]a[1]...a[n - 1] fits the second template's prefix of length j - 1" means that we can address to some state dp[...][j - 1], but what to do with the second part? We can first try to take care of the obvious cases: when the '*' in the first template corresponds to an empty string within the answer – in this case the length of the shortest such answer is just dp[i - 1][j].
And what remains to handle is only the case where '*' corresponds to at least one character, i.e. a[n - 1]. But in this case a[0]a[1]...a[n - 2] fits not only the second template's prefix of length j - 1, but also the first template's prefix of length i, moreover, there is a one-to-one correspondence between the objects that we are left to handle and the objects corresponding to the state dp[i][j - 1], each of the needed strings can be obtained by taking some of the strings corresponding to dp[i][j - 1] and adding the letter t[j - 1] (or, let's say, letter 'a' if t[j - 1] is a '?'). This means that the final formula for this case is dp[i][j] = min(dp[i - 1][j], dp[i][j - 1] + 1).
Implementation
The base states of the DP are those when i = 0 or j = 0, in this case dp[i][j] equals either 0 if every symbol in the prefixes is a '*' or inf otherwise. The time complexity is obviously O(|s| * |t|).
Another Example
607B - Zuma There is a sequence of numbers, you can delete a consecutive segment of this sequence if it is a palindrome. Find the minimum amount of such steps to delete the whole sequence.
Given the constraints, we can assume that the parameters are l and r, where dp[l][r] is the answer for this problem if we only had the half-interval of the sequence from l inclusively to r non-inclusively. Now we need to think, how can we find this value knowing all the values for the interior intervals. First of all, we need to determine what an object is in this case. Of course, by object we mean a set of actions that lead to removal of the whole string. Sometimes it's helpful to draw the object visually.
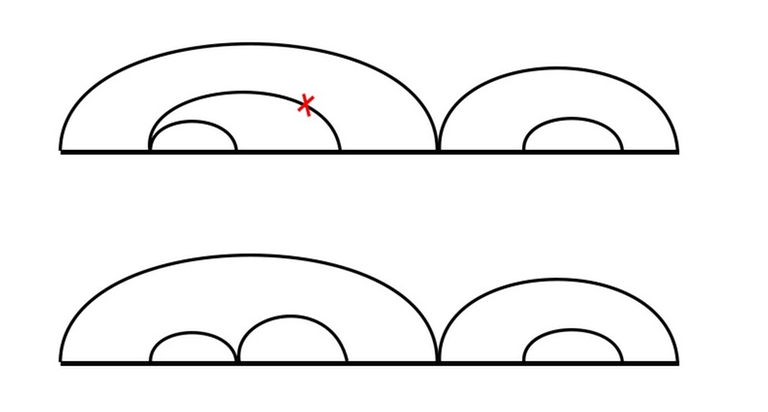
Let's draw an arc over the part of the sequence we are deleting. The arc will contain other arcs corresponding to previous removals of inner parts. Let's agree to not draw an arc from l to r if there is already an arc from l to r' (r' < r), in this case we could just as well draw it from r' to r (as the rest is deleted anyway). We do the similar if there is already an arc from l' to r (l < l'). This way we can ensure that the leftmost and the rightmost elements under the arc are deleted with the very action corresponding to the arc.
Let's follow our own advice and first take care of the obvious cases. What we can do is just apply all the transitions dp[l][r] = min(dp[l][r], dp[l][mid] + dp[mid][r]) (where l < mid < r), i.e. try to split the interval into two in all possible ways and remove them separately in an optimal way, fortunately the constraints allow us to do that.

The objects we didn't cover are the ones that can't be split in two independent parts, that is the ones with an arc covering the whole sequence, or the ones where the leftmost and the rightmost elements are deleted on the very last step. First of all, this implies that the leftmost and the rightmost elements are equal, as we can only delete palindromes. If they are not equal then we have already covered all the cases with the transitions we've made. Otherwise, we still need to find the shortest set of actions that ends with simultaneous removal of the leftmost and the rightmost elements of the interval. The last action is fixed and doesn't depend on us. A general advise: if something doesn't depend on you, try to acknowledge it and digress from it.
Let's re-formulate what objects we are looking for, but now without mentioning the last action: a set of stipulated actions on the segment of a sequence that don't affect the leftmost and the rightmost elements and leads to the sequence's segment becoming a palindrome (so that we can then make the last action: delete the whole segment). In other words we want to know what is the minimal amount of steps to make a half-interval [l + 1, r - 1) become a palindrome. But this is of course just dp[l + 1][r - 1] - 1, because every object corresponding to dp[l + 1][r - 1] is essentially a set of actions that lead to the segment becoming a palindrome and then one more action to delete it. So the final transition that we need to apply in case if c[l] = c[r - 1] is dp[l][r] = min(dp[l][r], dp[l + 1][r - 1]) (do the same set of actions, but in the end instead of the removing [l + 1, r - 1) remove [l, r)).
Note: our logic breaks if r - l = 2, in this case dp[l + 1][r - 1] = 0, so we can't replace the last action in the set. In this case dp[l][r] = 1 (if c[l] = c[r - 1]).
Implementation
The base states of the DP are those when r - l = 1, in this case dp[l][r] equals 1. The time complexity is O(n^3).
Conclusion
I hope I gave you some insight into how to easily come up with the transitions for a Subtask DP. If you enjoyed this post, please leave a like :)
If you want to know more, I remind that I do private lessons on competitive programming, the price is $25/h. Contact me on Telegram, Discord: rembocoder#3782, or in CF private messages.










