1678A - Tokitsukaze and All Zero Sequence
Idea: tokitsukaze
Prepare: tokitsukaze
We observe that when there is $$$0$$$ in the sequence, it is optimal to choose $$$0$$$ and any number other than $$$0$$$ for each operation.
Therefore, when there is $$$0$$$ in the sequence, let $$$cnt$$$ be the number of $$$0$$$s, the answer is $$$n - cnt$$$.
Otherwise, when $$$0$$$ does not exist in the sequence, there are two situations:
When there exist two equal numbers in the sequence, we can perform the operation $$$1$$$ time to convert it into the situation of having $$$0$$$ in the sequence. So the answer must be $$$n$$$.
When all numbers in the sequence are distinct, we can perform the operation $$$2$$$ times to convert it into the situation of having $$$0$$$ in the sequence. So the answer must be $$$n + 1$$$.
#include <bits/stdc++.h>
using namespace std;
int main(){
int t;
scanf("%i",&t);
while(t--){
int n;
scanf("%i",&n);
vector<int> a(n);
for(int i=0;i<n;i++)
scanf("%i",&a[i]);
sort(a.begin(),a.end());
int zero=count(a.begin(),a.end(),0);
if(zero>0)
printf("%i\n",n-zero);
else{
bool same=false;
for(int i=1;i<n;i++)
if(a[i]==a[i-1])
same=true;
if(same)printf("%i\n",n);
else printf("%i\n",n+1);
}
}
return 0;
}
1678B1 - Tokitsukaze and Good 01-String (easy version) and 1678B2 - Tokitsukaze and Good 01-String (hard version)
Idea: qsmcgogo-B1, 74TrAkToR-B2
Prepare: tokitsukaze
Obviously, the operation is, for each pair of adjacent and unequal characters, change both of them to $$$0$$$ or $$$1$$$. In other words, the string is divided into many adjacent binaries with length of $$$2$$$. If the binary is "01" or "10", it needs $$$1$$$ operation, otherwise the operation is not required.
If you want to minimize the number of "contiguous segments", a simple greedy way is to change each "binary requiring operation" (i.e. $$$01$$$ or $$$10$$$) into the form of the previous or next "binary requiring no operation" (i.e. $$$11$$$ or $$$00$$$). For example: "0010" change to "0000" and "1101" change to "1111". In this way, this "binary requiring operation" has no contribution to the final number of contiguous segments. We only need to count the number of contiguous "11" and "00" binaries.
In particular, if all binaries are "01" or "10", the final contribution to the number of final contiguous segments is $$$1$$$ in total.
Obviously, the operation is, for each pair of adjacent and unequal characters, change both of them to $$$0$$$ or $$$1$$$. In other words, the string is divided into many adjacent binaries with length of $$$2$$$.
Consider the recursion from the front to the back, it can be observed that the previously maintained prefix must end with "00" or "11". Therefore, it's necessary to convert each divided binary into "00" or "11" by enumerating the cost of changing the current binary into "00" and "11". Maintain the minimum number of operations in the process of DP, try to make the current string consistent with the end of the prefix subsegment.
$$$dp[n][2]$$$, set the first dimension as the maintained length of prefix and the second dimension as the suffix state of the prefix.
Then the DP transfer equation is:
where $$$c_k$$$ represents the cost of converting the current binary to "kk".
#include <bits/stdc++.h>
using namespace std;
using LL = long long;
int main() {
ios::sync_with_stdio(false);
cin.tie(nullptr);
int t;
for (cin >> t; t; t -= 1) {
int n, L = -1, x = 0, y = 0;
string s;
cin >> n >> s;
for (int i = 0; i < n; i += 2) {
if (s[i] != s[i + 1]) x += 1;
else {
if (L != s[i]) y += 1;
L = s[i];
}
}
cout << x << " " << max(y, 1) << "\n";
}
}
#include<bits/stdc++.h>
#define fre(z) freopen(z".in","r",stdin),freopen(z".out","w",stdout)
#define lowit(x) (x&-x)
#define range(x) begin(x), end(x)
#define sz(x) (int)(x).size()
#define pb push_back
#define sto \
std::ios::sync_with_stdio(false); \
std::cin.tie(nullptr); \
std::cout.tie(nullptr);
using namespace std;
typedef long long ll;
typedef pair<ll,ll> PII;
inline ll read(){
ll x=0;char ch;bool f=true;
for(ch=getchar();!isdigit(ch);ch=getchar())if(ch=='-')f^=f;
for(;isdigit(ch);ch=getchar())x=(x<<3)+(x<<1)+(ch^48);
return f?x:-x;
}
//#define LOCAL_DEFINE
#define DEBUG(x) cerr<<(#x)<<'='<<(x)<<endl
const int N=2e5+7;
const int INF=1e9;
char s[N];
int c[N];
PII dp[N][2];
void solve(){
int n=read();
scanf("%s",s+1);
for(int i=1;i<=n;i++)s[i]-='0';
for(int i=1;i<=n/2;i++)c[i]=s[i*2]+s[i*2-1]*2;
for(int i=1;i<=n/2;i++)for(int j=0;j<2;j++)dp[i][j]={INF,INF};
for(int i=1;i<=n/2;i++)for(int j=0;j<2;j++){
int cc=c[i],dd=j?3:0,cnt=((dd%2)^(cc%2))+((dd/2)^(cc/2));
for(int k=0;k<2;k++)
dp[i][j]=min(dp[i][j],{dp[i-1][k].first+cnt,dp[i-1][k].second+(j!=k)});
}
PII ans=min(dp[n/2][0],dp[n/2][1]);
cout<<ans.first<<" "<<ans.second+1<<"\n";
}
int main(){
#ifdef ONLINE_JUDGE
#else
//fre("1");
#endif
ll T=1;
T=read();
for(int i=1;i<=T;i++)solve();
#ifdef LOCAL_DEFINE
cerr << "Time elapsed: " << 1.0 * clock() / CLOCKS_PER_SEC << " s.\n";
#endif
return 0;
}
1677A - Tokitsukaze and Strange Inequality
Idea: tokitsukaze
Prepare: tokitsukaze
We can calculate the answer in two steps.
The first step, for each $$$b$$$, let $$$f_b$$$ represents the number of $$$p_d$$$ where $$$p_b > p_d$$$ in the interval $$$[b+1,n]$$$. We can calculate $$$f$$$ in $$$\mathcal{O}(n^2)$$$.
The second step, calculate the answer. First we enumerate $$$c$$$ from $$$1$$$ to $$$n$$$, and then enumerate $$$a$$$ from $$$1$$$ to $$$c-1$$$. When $$$p_a < p_c$$$, add $$$f_b$$$ in the interval $$$[a+1,c-1]$$$ to the answer. Before enumerating $$$a $$$, we can calculate the prefix sum of $$$f$$$ first, so we can add the $$$f_b$$$ in the interval to the answer in $$$\mathcal{O}(1)$$$. The time complexity of this step is $$$\mathcal{O}(n^2)$$$. However, this will add the result of $$$d$$$ in the interval $$$[a+1,c-1]$$$ to the answer, which is illegal because $$$c < d$$$ is required. So we need to maintain $$$f$$$ while enumerating $$$c$$$: enumerate $$$b$$$ from $$$1$$$ to $$$c-1$$$, if $$$p_b > p_c$$$, $$$f_b$$$ minus $$$1$$$. $$$p_c$$$ is actually regarded as $$$p_d$$$, that is, subtract the case where $$$c$$$ is equal to $$$d$$$, so as to subtract the illegal case. The time complexity of this step is also $$$\mathcal{O}(n^2)$$$.
Time complexity:$$$\mathcal{O}(n^2)$$$.
By the way, use Fenwick Tree or Segment Tree can also pass, the time complexity is $$$\mathcal{O}(n^2 log\ n)$$$
#include <bits/stdc++.h>
using namespace std;
/************* debug begin *************/
string to_string(string s){return '"'+s+'"';}
string to_string(const char* s){return to_string((string)s);}
string to_string(const bool& b){return(b?"true":"false");}
template<class T>string to_string(T x){ostringstream sout;sout<<x;return sout.str();}
template<class A,class B>string to_string(pair<A,B> p){return "("+to_string(p.first)+", "+to_string(p.second)+")";}
template<class A>string to_string(const vector<A> v){
int f=1;string res="{";for(const auto x:v){if(!f)res+= ", ";f=0;res+=to_string(x);}res+="}";
return res;
}
void debug_out(){puts("");}
template<class T,class... U>void debug_out(const T& h,const U&... t){cout<<" "<<to_string(h);debug_out(t...);}
#ifdef tokitsukaze
#define debug(...) cout<<"["<<#__VA_ARGS__<<"]:",debug_out(__VA_ARGS__);
#else
#define debug(...) 233;
#endif
/************* debug end *************/
#define mem(a,b) memset((a),(b),sizeof(a))
#define MP make_pair
#define pb push_back
#define fi first
#define se second
#define sz(x) (int)x.size()
#define all(x) x.begin(),x.end()
#define sqr(x) (x)*(x)
using namespace __gnu_cxx;
typedef long long ll;
typedef unsigned long long ull;
typedef pair<int,int> PII;
typedef pair<ll,ll> PLL;
typedef pair<int,ll> PIL;
typedef pair<ll,int> PLI;
typedef vector<int> VI;
typedef vector<ll> VL;
typedef vector<PII > VPII;
/************* define end *************/
void println(VI x){for(int i=0;i<sz(x);i++) printf("%d%c",x[i]," \n"[i==sz(x)-1]);}
void println(VL x){for(int i=0;i<sz(x);i++) printf("%lld%c",x[i]," \n"[i==sz(x)-1]);}
void println(int *x,int l,int r){for(int i=l;i<=r;i++) printf("%d%c",x[i]," \n"[i==r]);}
void println(ll *x,int l,int r){for(int i=l;i<=r;i++) printf("%lld%c",x[i]," \n"[i==r]);}
/*************** IO end ***************/
void go();
int main(){
#ifdef tokitsukaze
freopen("TEST.txt","r",stdin);
#endif
go();return 0;
}
const int INF=0x3f3f3f3f;
const ll LLINF=0x3f3f3f3f3f3f3f3fLL;
const double PI=acos(-1.0);
const double eps=1e-6;
const int MAX=1e5+10;
const ll mod=998244353;
/********************************* head *********************************/
int a[MAX];
ll f[MAX],bitf[MAX];
void go()
{
int n,i,j,k,l,T;
ll ans;
scanf("%d",&T);
while(T--)
{
scanf("%d",&n);
for(i=1;i<=n;i++) scanf("%d",&a[i]);
mem(f,0);
for(j=1;j<=n;j++)
{
for(l=j+1;l<=n;l++)
{
if(a[j]>a[l]) f[j]++;
}
}
ans=0;
for(k=1;k<=n;k++)
{
for(j=1;j<k;j++)
{
if(a[j]>a[k]) f[j]--;
}
bitf[0]=0;
for(i=1;i<=k;i++) bitf[i]=bitf[i-1]+f[i];
for(i=1;i<k;i++)
{
if(a[i]<a[k]) ans+=bitf[k-1]-bitf[i];
}
}
printf("%lld\n",ans);
}
}
1677B - Tokitsukaze and Meeting
Idea: funer
Prepare: tokitsukaze, funer
Obviously, we can calculate the answers of rows and columns separately.
For the answers of columns, we can observe that since there are only $$$n \cdot m$$$ students in total, no students will leave, and every time a new student entering the meeting hall, all columns will move one step to the right circularly, so the answer will not decrease. If the $$$i$$$-th student is a serious student, for all the previous students with subscript $$$j$$$ where $$$0 < j < i$$$, and $$$j \% m = i \% m$$$ are naughty students, the answer in the column will increase by $$$1$$$.
For the answer of rows, we can transfer it from the answer of $$$i-m$$$, which is equivalent to adding a new row to the answer of $$$i-m$$$. Suppose the last serious student is the $$$j$$$-th student. If $$$i-j<m$$$, the answer will increase by $$$1$$$, otherwise the answer will be the same as that of when the $$$i-m$$$ student enters the meeting hall.
#include<bits/stdc++.h>
using namespace std;
int rownum[1000100];
int col[1000100];
int n,m;
void init(){
for(int i = 0;i <= max(n,m);i++) {
rownum[i] = col[i] = 0;
}
}
void solve(){
scanf("%d%d",&n,&m);
init();
int las = -n*m;
int colnum = 0;
char tmp;
for(int i = 0;i < n*m;i++) {
scanf(" %c",&tmp);
tmp -= '0';
if(tmp == 1) {
las = i;
if(col[i%m] == 0) {
col[i%m] = 1;
colnum++;
}
}
if(i - las < m) {
rownum[i%m]++;
}
if(i!=0) printf(" ");
printf("%d",rownum[i%m] + colnum);
}
printf("\n");
}
int main(){
int T;
scanf("%d",&T);
while(T--) {
solve();
}
}
1677C - Tokitsukaze and Two Colorful Tapes
Idea: qsmcgogo, winterzz1
Prepare: winterzz1
First, find the cycle directly, take out all the cycles, and then fill each cycle in the order: maximum, minimum, maximum, minimum $$$ \ldots $$$.
Note that when you encounter an odd cycle, the last one should be empty and fill in the middle value.
For example, in a ternary cycle, if the first and the second position are filled with $$$1$$$ and $$$9$$$, it can be observed that the contribution of the ternary cycle to the answer remains unchanged no matter which number between $$$2 \sim 8$$$ is filled in the middle. So this situation can be left out first, and finally fill in whatever number is left. The same to the cycles with odd sizes such as self cycles and five membered cycles, because the last number does not provide any contribution. In this way, you can directly construct a solution with the maximum $$$score$$$.
We notice that if we take out the numbers that has already been filled in each cycle and put them into a new cycled array $$$h$$$, in fact, the numbers providing contribution are only at the "peak" and "valley" points of the array. We define "peak" as the point with subscript $$$i$$$ where $$$h_{i}>h_{i-1}$$$ and $$$h_{i}>h_{i+1}$$$, and "valley" is the point with subscript $$$i$$$ where $$$h_{i}<h_{i-1}$$$ and $$$h_{i}<h_{i+1}$$$. Obviously, each "peak" will provide contribution of $$$2 \cdot h_{i}$$$, each "valley" will provide contribution of $$$-2 \cdot h_{i}$$$. For the points which are neither "peak"s nor "valley"s, they do not provide any contribution.
In order to maximize the score, we make the larger number in the permutation "peak" and the smaller number "valley". There are $$$\left \lfloor \frac{CircleSize}{2} \right \rfloor$$$ "peak"s and "valley"s for a circle with a length of $$$Circlesize$$$.
So the expression of the final answer can be derived from the summation formula of the arithmetic sequence:
Let $$$c=\sum \left \lfloor \frac{CircleSize}{2} \right \rfloor$$$, $$$N$$$ represents the size of the permutation, $$$score=2c \cdot (N-c)$$$.
#include <bits/stdc++.h>
using namespace std;
const int MAXN = 100005;
int n,col[2][MAXN],col_to_pos_1[MAXN];
long long output;
bool vis_0[MAXN];
int T,cnt;
long long c;
void dfs(int pos)
{
if(vis_0[pos])return;
vis_0[pos]=true;
++cnt;
dfs(col_to_pos_1[col[0][pos]]);
}
int main(int argc, char const *argv[])
{
scanf("%d",&T);
while(T--)
{
scanf("%d",&n);
for(int i=1;i<=n;++i)
{
vis_0[i]=false;
}
for(int i=1;i<=n;++i)
{
scanf("%d",&col[0][i]);
}
for(int i=1;i<=n;++i)
{
scanf("%d",&col[1][i]);
col_to_pos_1[col[1][i]]=i;
}
c=0;
for(int i=1;i<=n;++i)
{
cnt=0;
dfs(i);
c+=cnt/2;
}
printf("%lld\n", (c*(n-c))<<1);
}
return 0;
}
1677D - Tokitsukaze and Permutations
Idea: dark_light, FreshP_0325
Prepare: dark_light
Consider finding out the relationship between sequence $$$v$$$ and permutation $$$p$$$. It can be observed that the permutation $$$p$$$ have bijective relationship with sequence $$$c$$$. That is to say, sequence $$$c$$$ will only correspond to one permutation $$$p$$$, as it can be proved:
Let $$$S={1,2,\ldots,n}$$$, and find that the last number can be determined through $$$c_n$$$, because there is no number after this position. We observe that $$$p_n$$$ is the $$$(c_n+1)$$$ largest number in $$$S$$$, then delete $$$p_n$$$ from $$$S$$$, we can get $$$p_{n - 1}$$$. So repeat the process, we can get the whole permutation.
Consider counting $$$v$$$, we observe that each bubble sort will first make $$$v_i=\max(v_{i}-1,0)$$$, then the whole $$$v$$$ moves left, $$$v_1$$$ is directly covered, $$$v_n$$$ is set to $$$0$$$. Because each valued $$$v_i$$$ is preceded by a number larger than the current position, then it will definitely be exchanged and moved forward, $$$v_i$$$ minus $$$1$$$.
For example, if the current $$$v=[0,0,2,1,1]$$$, after once bubble sort, $$$v=[0,1,0,0,0]$$$.
To avoid confusion, the $$$V$$$ array below is the $$$v$$$ in the input. It's easy to count after knowing the above conclusion.
For the position $$$i(i\le k)$$$, it can be observed that after $$$k$$$ times of bubble sort , it is directly covered, so just multiply the answer by $$$\prod_{i=1}^k i$$$.
For the position $$$i(k\lt i \le n)$$$, if $$$V_{i-k}\ne -1$$$, then obviously $$$v_i$$$ is uniquely determined; If $$$V_{i-k}=-1$$$, then $$$v_i$$$ has $$$i$$$ possible values, multiply the answer by $$$i$$$; If $$$V_{i-k}=0$$$, then $$$v_i-k\le 0$$$, multiply the answer by $$$k+1$$$.
Note that for the position $$$i(i\ge n-k+1)$$$, $$$V_i$$$ should be $$$0$$$ or $$$-1$$$, otherwise the answer must be $$$0 $$$.
Complexity:$$$\mathcal{O}(n)$$$.
#include<cstdio>
#include<iostream>
#include<cstring>
#include<algorithm>
#include<queue>
#include<map>
#include<ctime>
#include<cmath>
#include<unordered_map>
using namespace std;
#define LL long long
#define pp pair<int,pair<int,int>>
#define mp make_pair
#define fi first
#define se second.first
#define th second.second
namespace IO{
const int sz=1<<22;
char a[sz+5],b[sz+5],*p1=a,*p2=a,*t=b,p[105];
inline char gc(){
return p1==p2?(p2=(p1=a)+fread(a,1,sz,stdin),p1==p2?EOF:*p1++):*p1++;
}
template<class T> void gi(T& x){
x=0; int f=1;char c=gc();
if(c=='-')f=-1;
for(;c<'0'||c>'9';c=gc())if(c=='-')f=-1;
for(;c>='0'&&c<='9';c=gc())
x=x*10+(c-'0');
x=x*f;
}
inline void flush(){fwrite(b,1,t-b,stdout),t=b; }
inline void pc(char x){*t++=x; if(t-b==sz) flush(); }
template<class T> void pi(T x,char c='\n'){
if(x==0) pc('0'); int t=0;
for(;x;x/=10) p[++t]=x%10+'0';
for(;t;--t) pc(p[t]); pc(c);
}
struct F{~F(){flush();}}f;
}
using IO::gi;
using IO::pi;
using IO::pc;
int t,n,a[1000005],ans,k;
const int mod=998244353;
signed main(){
srand(time(0));
gi(t);
while(t--){
gi(n),gi(k);
bool f=0;
for(int i=1;i<=n;i++)gi(a[i]),f|=(a[i]>i-1);
if(f){
pi(0,'\n');
continue;
}
ans=1;
for(int i=1;i<=k;i++)ans=1ll*ans*i%mod;
for(int i=n-k+1;i<=n;i++){
if(a[i]!=-1&&a[i]){
pi(0,'\n');
f=1;
break;
}
}
if(f)continue;
for(int i=k+1;i<=n;i++){
int limit=i-1;
if(a[i-k]==-1){
ans=1ll*ans*i%mod;
}else{
if(a[i-k]){
limit=a[i-k]+k;
if(limit>i-1)f=1;
}
else {
limit=min(limit,k),ans=1ll*ans*(limit+1)%mod;
}
}
}
if(f)ans=0;
pi(ans,'\n');
}
return 0;
}
1677E - Tokitsukaze and Beautiful Subsegments
Idea: Frank_DD
Prepare: Frank_DD
Let's sort the queries $$$[l,r]$$$ with $$$r$$$ in ascending order.
Let's move $$$R$$$ from $$$1$$$ to $$$n$$$, and answer queries $$$[l,r]$$$ when $$$r=R$$$.
Use segment tree to solve this problem, each leaf node $$$[ul,ul]$$$ in the segment tree maintenance the number that how many intervals $$$[ul,R]$$$ are beautiful, then answering queries is to get sum.
Use monotone stack to maintain the maximum number. When moving $$$R$$$ one step right, the monotone stack will pop some and push one.
Let's think about the number $$$x$$$ in monotone stack, which means the maximum number of the intervals $$$[lp,R]$$$ ($$$l1 \le lp \le l2$$$) is $$$x$$$. If there exist a $$$ll$$$ in $$$[l1,l2]$$$ which satisfies $$$a_{ll}*a_R=x$$$, then before $$$x$$$ is poped, intervals $$$[l,rr]$$$ are beautiful($$$l \in [l1,l2]$$$,$$$l \le ll$$$ ,$$$R \le rr$$$).
So we can assume that $$$x$$$ will not be poped when it is pushed in the monotone stack, and do something like difference algorithm in the segment tree, by using the current $$$R$$$ as the time stamp. Each node in the segment tree has to maintain $$$a*R+b$$$,which like a linear function.
So when moving $$$R$$$ right step, let's enumerate the factor of $$$a_R$$$ to update old intervals in monotone stack, enumerate the multiple of $$$a_R$$$ to update the new interval in monotone stack and update the intervals which are poped.
Time complexity: $$$\mathcal{O}(nlognlogn+qlogn)$$$.
#include<bits/stdc++.h>
using namespace std;
const int N=2e5+5;
typedef pair<int,int> pp;
int n,m,ti,top,a[N],d[N],p[N],bz[N],bo[N];
long long ans[1000005];
vector<pp>q[1000005];
vector<int>w[N];
struct dd
{
long long x,y,tg,len;
}tr[N*4];
void make(int x,int l,int r)
{
tr[x].len=r-l+1;
if (l==r) return;
int mid=l+r>>1;
make(x<<1,l,mid),make(x<<1|1,mid+1,r);
}
void down(int x)
{
if (tr[x].x==tr[x].len)
{
tr[x<<1].x=tr[x<<1].len;
tr[x<<1|1].x=tr[x<<1|1].len;
}
if (tr[x].x==0)
{
tr[x<<1].x=0;
tr[x<<1|1].x=0;
}
tr[x<<1].tg+=tr[x].tg;
tr[x<<1].y+=tr[x].tg*tr[x<<1].len;
tr[x<<1|1].tg+=tr[x].tg;
tr[x<<1|1].y+=tr[x].tg*tr[x<<1|1].len;
tr[x].tg=0;
}
void up(int x)
{
tr[x].x=tr[x<<1].x+tr[x<<1|1].x;
tr[x].y=tr[x<<1].y+tr[x<<1|1].y;
}
void clear(int x,int l,int r,int ll,int rr)
{
if (l>=ll && r<=rr)
{
tr[x].tg+=ti;
tr[x].y+=ti*tr[x].len;
tr[x].x=0;
return;
}
down(x);
int mid=l+r>>1;
if (ll<=mid) clear(x<<1,l,mid,ll,rr);
if (rr>mid) clear(x<<1|1,mid+1,r,ll,rr);
up(x);
}
void add(int x,int l,int r,int ll,int rr)
{
if (l>=ll && r<=rr)
{
tr[x].tg-=ti;
tr[x].x=tr[x].len;
tr[x].y-=ti*tr[x].len;
return;
}
down(x);
int mid=l+r>>1;
if (ll<=mid) add(x<<1,l,mid,ll,rr);
if (rr>mid) add(x<<1|1,mid+1,r,ll,rr);
up(x);
}
long long find(int x,int l,int r,int ll,int rr)
{
if (l>=ll && r<=rr) return tr[x].y+ti*tr[x].x;
down(x);
int mid=l+r>>1;
long long ans=0;
if (ll<=mid) ans+=find(x<<1,l,mid,ll,rr);
if (rr>mid) ans+=find(x<<1|1,mid+1,r,ll,rr);
return ans;
}
int main()
{
//freopen("a.in","r",stdin);
//freopen("1.out","w",stdout);
scanf("%d%d",&n,&m);
for (int i=1;i<=n;i++) scanf("%d",&a[i]),bz[a[i]]=i;
for (int i=1;i<=m;i++)
{
int l,r;
scanf("%d%d",&l,&r);
q[r].emplace_back(l,i);
}
for (int i=1;i<=n;i++)
for (int j=i;j<=n;j+=i)
w[j].emplace_back(i);
make(1,1,n);
for (int i=1;i<=n;i++)
{
while (top && a[d[top]]<a[i])
{
if (p[top]>d[top-1]) clear(1,1,n,d[top-1]+1,p[top]);
bo[d[top]]=0;
top--;
}
for (int j=a[i];j<=n;j+=a[i])
if (bo[bz[j]])
{
int pt=bo[bz[j]];
int l=d[pt-1]+1,r=d[pt];
int e=bz[j/a[i]];
if (e<l || e>=i) continue;
e=min(e,r);
if (e<=p[pt]) continue;
// if (l<=p[pt]) clear(1,1,n,l,p[pt]);
add(1,1,n,p[pt]+1,e);
p[pt]=e;
}
d[++top]=i;
bo[i]=top;
p[top]=d[top-1];
for (auto j:w[a[i]])
{
int l=d[top-1]+1,r=i;
int e1=bz[j],e2=bz[a[i]/j];
if (e2<=e1) continue;
if (e1<l || e2>i) continue;
if (e1<=p[top]) continue;
// if (l<=p[top]) clear(1,1,n,l,p[top]);
add(1,1,n,p[top]+1,e1);
p[top]=e1;
}
ti++;
for (auto t:q[i]) ans[t.second]=find(1,1,n,t.first,i);
}
for (int i=1;i<=m;i++) printf("%lld\n",ans[i]);
return 0;
}
Idea: dark_light
Prepare: dark_light
First, consider how to calculate the contribution of a legal path. It can be found that the contribution of a legal path is equivalent to the following formula, where $$$b_i$$$ indicates the number of the $$$i$$$-th gems on the path.
This formula seems impossible to calculate, but it can be observed that there is a chain structure behind it. Consider dynamic programming, try to calculate the $$$1\sim (i+1)$$$-th gems' answer by only considering the $$$1\sim i$$$-th gems' answer. Consider maintenance these:
$$$dp_{n,1}=\sum_{i_1=0}^{b_1}\sum_{i_2=0}^{b_2}\ldots \sum_{i_n=0}^{b_n}(\sum_{j=1}^n (P^{i_j}i_j^k)\times\sum_{j=1}^n [i_j\ne 0])$$$
$$$dp_{n,2}=\sum_{i_1=0}^{b_1}\sum_{i_2=0}^{b_2}\ldots \sum_{i_n=0}^{b_n}\sum_{j=1}^n (P^{i_j}i_j^k)$$$
$$$dp_{n,3}=\sum_{i_1=0}^{b_1}\sum_{i_2=0}^{b_2}\ldots \sum_{i_n=0}^{b_n} \sum_{j=1}^n [i_j\ne 0]$$$
$$$dp_{n,4}=\sum_{i_1=0}^{b_1}\sum_{i_2=0}^{b_2}\ldots \sum_{i_n=0}^{b_n} 1$$$
It can be observed that if we enumerate how many the $$$(n + 1)$$$-th gem are selected, this can actually be transferred, for example:
$$$dp_{n+1,1}=\sum_{p=0}^{b_{n+1}}\sum_{i_1=0}^{b_1}\sum_{i_2=0}^{b_2}\ldots \sum_{i_n=0}^{b_n}((\sum_{j=1}^n P^{i_j}i_j^k+P^p p^k)\times (\sum_{j=1}^n [i_j\ne 0])+[p\ne 0])$$$
Then spread.
$$$A=\sum_{p=0}^{b_{n+1}}\sum_{i_1=0}^{b_1}\sum_{i_2=0}^{b_2}\ldots \sum_{i_n=0}^{b_n}(\sum_{j=1}^n P^{i_j}i_j^k \times \sum_{j=1}^n [i_j\ne 0])=(1+b_{n+1})dp_{n,1}$$$
$$$B=\sum_{p=0}^{b_{n+1}}\sum_{i_1=0}^{b_1}\sum_{i_2=0}^{b_2}\ldots \sum_{i_n=0}^{b_n}\sum_{j=1}^n P^{i_j}i_j^k[p\ne 0]=b_{n+1}dp_{n,2}$$$
$$$C=\sum_{p=0}^{b_{n+1}}\sum_{i_1=0}^{b_1}\sum_{i_2=0}^{b_2}\ldots \sum_{i_n=0}^{b_n}P^p p^k\times \sum_{j=1}^n [i_j\ne 0]=dp_{n,3} \times \sum_{p=0}^{b_{n+1}}P^p p^k=dp_{n,3} \times \sum_{p=1}^{b_{n+1}}P^p p^k$$$
$$$D=\sum_{p=0}^{b_{n+1}}\sum_{i_1=0}^{b_1}\sum_{i_2=0}^{b_2}\ldots \sum_{i_n=0}^{b_n}(P^p p^k)\times [p\ne 0]=dp_{n,4}\times\sum_{p=1}^{b_{n+1}}P^p p^k$$$
Now it can be transferred. The main problem is how to calculate $$$\sum_{i=1}^n i^kx^i$$$ quickly, ensuring that $$$x\gt 1$$$.
Let $$$h_{k,n}$$$ represent $$$\sum_{i=1}^n i^k x^i$$$.
Calculate the sum according to the proportional sequence, $$$h_{0,n}=\dfrac{x^{n+1}-x}{x-1}$$$.
Finally we get
According to this recurrence formula, we can get
When $$$k$$$ is constant, there exist a $$$k$$$-degree polynomial $$$g_k(x)$$$ about $$$n$$$, making $$$h_{k,n}=x^{n+1}g_k(n)-xg_k(0)$$$. This conclusion can be proved by mathematical induction.
Consider how to use interpolation to get this polynomial, we only need to find $$$g_k(0)\sim g_k(k)$$$.
Consider difference method, $$$h_{k,n}-h_{k,n-1}=x^{n+1}g_k(n)-x^ng_k(n-1)=n^kx^n$$$.
So $$$xg_k(n)-g_k(n-1)=n^k$$$. But we still can't get $$$C$$$. There is a conclusion: the $$$(n + 1)$$$-th difference of the $$$n$$$-degree polynomial $$$f(x)$$$ is $$$0$$$. That is to say, $$$\sum_{i=0}^{n+1}(-1)^{n+1-i}\binom{n+1}{i}f(i)=0$$$.
So we can get $$$g_k(0)$$$, then use polynomial fast interpolation, and then polynomial multipoint evaluation to get the value of every point we need.
It can be observed that the DP transfer can be replaced by matrix, so there are matrices each position, the problem is equivalent to get the sum of the matrix products of all intervals. It's easy to solve. You can solve it in the way you like.
Overall complexity: $$$\mathcal{O}(k\log^2k+n)$$$.
#include<cmath>
#include<queue>
#include<cstdio>
#include<cstring>
#include<assert.h>
#include<iostream>
#include<algorithm>
using namespace std;
#define LL long long
#define int long long
const int MAXN=4e5+5;
const int MAXNN=1e5+5;
int n,k,P,fac[MAXN],ifac[MAXN],Inv[MAXN],rev[MAXN],x[MAXN],y[MAXN],K[MAXN],B[MAXN],g[MAXN],F[MAXN],Q[MAXN],val[MAXN];
int a[MAXNN],b[MAXNN],W[21][MAXN*2];
const int mod=998244353;
vector<int>G[MAXNN];
inline int mul(int a,int b){return 1ll*a*b%mod;}
inline int dec(int a,int b){return ((a-b)%mod+mod)%mod;}
inline int add(int a,int b){return ((a+b)%mod+mod)%mod;}
inline int qkpow(int a,int b){
int ans=1,base=a;
while(b){
if(b&1)ans=mul(ans,base);
base=mul(base,base);
b>>=1;
}
return ans;
}
namespace IO{
const int sz=1<<22;
char a[sz+5],b[sz+5],*p1=a,*p2=a,*t=b,p[105];
inline char gc(){
return p1==p2?(p2=(p1=a)+fread(a,1,sz,stdin),p1==p2?EOF:*p1++):*p1++;
}
template<class T> void gi(T& x){
x=0; char c=gc();
for(;c<'0'||c>'9';c=gc());
for(;c>='0'&&c<='9';c=gc())
x=x*10+(c-'0');
}
inline void flush(){fwrite(b,1,t-b,stdout),t=b; }
inline void pc(char x){*t++=x; if(t-b==sz) flush(); }
template<class T> void pi(T x,char c='\n'){
if(x==0) pc('0'); int t=0;
for(;x;x/=10) p[++t]=x%10+'0';
for(;t;--t) pc(p[t]); pc(c);
}
struct F{~F(){flush();}}f;
}
using IO::gi;
using IO::pi;
using IO::pc;
const int S=4;
struct Matrix{
int a[4][4];
Matrix(){memset(a,0,sizeof a);}
void clear(){memset(a,0,sizeof a);}
void init(){for(int i=0;i<S;i++)a[i][i]=1;}
int* operator [] (int x){return a[x];}
Matrix friend operator +(Matrix A,Matrix B){
Matrix ret=Matrix();
for(int i=0;i<S;i++)
for(int j=0;j<=i;j++)
ret[i][j]=add(A[i][j],B[i][j]);
return ret;
}
Matrix friend operator -(Matrix A,Matrix B){
Matrix ret=Matrix();
for(int i=0;i<S;i++)
for(int j=0;j<=i;j++)
ret[i][j]=dec(A[i][j],B[i][j]);
return ret;
}
Matrix friend operator *(Matrix A,Matrix B){
Matrix ret=Matrix();
for(int k=0;k<S;k++)
for(int j=0;j<=k;j++)
if(B[k][j])
for(int i=k;i<S;i++)
ret[i][j]=1ll*(ret[i][j]+1ll*A[i][k]*B[k][j])%mod;
return ret;
}
Matrix friend operator *(Matrix A,int x){
Matrix ret=Matrix();
for(int i=0;i<S;i++)
for(int j=0;j<=i;j++)
ret[i][j]=1ll*A[i][j]*x%mod;
return ret;
}
}d[MAXNN],dp[MAXNN],ans;
Matrix operator += (Matrix &p,Matrix q){return p=p+q;}
Matrix operator -= (Matrix &p,Matrix q){return p=p-q;}
Matrix operator *= (Matrix &p,Matrix q){return p=p*q;}
inline int C(int n,int m){
if(n<m||m<0)return 0;
return 1ll*fac[n]*ifac[m]%mod*ifac[n-m]%mod;
}
void init(){
fac[0]=ifac[0]=Inv[0]=Inv[1]=1;
for(int i=1;i<MAXN;i++)fac[i]=1ll*fac[i-1]*i%mod;
ifac[MAXN-1]=qkpow(fac[MAXN-1],mod-2);
for(int i=MAXN-2;i>=1;i--)ifac[i]=1ll*ifac[i+1]*(i+1)%mod;
for(int i=2;i<MAXN;i++)Inv[i]=1ll*(mod-mod/i)*Inv[mod%i]%mod;
int wn;
for(int i=0,x=1;x<MAXN;i++,x<<=1){
W[i][x]=1;
wn=qkpow(3,(mod-1)/(x<<1));
for(int j=1;j<x;j++)W[i][x+j]=1ll*wn*W[i][x+j-1]%mod;
wn=qkpow(wn,mod-2);
for(int j=1;j<x;j++)W[i][x-j]=1ll*wn*W[i][x-j+1]%mod;
}
}
inline void NTT(int *a,int type,int n){
for(int i=0;i<n;i++)if(i<rev[i])swap(a[i],a[rev[i]]);
LL x,y;
for(int i=1,cnt=0;i<n;cnt++,i<<=1){
for(int j=0;j<n;j+=(i<<1)){
for(int t=0,k=j;k<j+i;k++,t+=type){
x=a[k],y=1ll*W[cnt][i+t]*a[k+i];
a[k]=(x+y)%mod;
a[k+i]=(x-y)%mod;
}
}
}
if(type==-1)for(int i=0;i<n;i++)a[i]=mul(a[i],Inv[n]);
}
void Polyinv(int *a,int *b,int len){
static int c[MAXN];
if(len==1){
b[0]=qkpow(a[0],mod-2);
return ;
}
Polyinv(a,b,(len+1)>>1);
int l=0,m=(len<<1),n=1;
for(;n<=m;n<<=1,l++);
for(int i=0;i<n;i++)rev[i]=(rev[i>>1]>>1)|((i&1)<<(l-1));
for(int i=0;i<len;i++)c[i]=a[i];
for(int i=len;i<n;i++)c[i]=0;
NTT(c,1,n),NTT(b,1,n);
for(int i=0;i<n;i++)b[i]=1ll*(2-1ll*b[i]*c[i])%mod*b[i]%mod;
NTT(b,-1,n);
for(int i=len;i<n;i++)b[i]=0;
}
inline void Polydao(int *Aa,int *Bb,int len){
Bb[len-1]=0;
for(int i=1;i<len;i++)Bb[i-1]=1ll*i*Aa[i]%mod;
}
int init_NTT(int L){
int l=0,m=L,n=1;
for(;n<=m;n<<=1,l++);
for(int i=0;i<n;i++)rev[i]=(rev[i>>1]>>1)|((i&1)<<(l-1));
return n;
}
void MUL(int *a,int *b,int *c,int n,int m,int lim){
static int t1[MAXN],t2[MAXN],t3[MAXN];
for(int i=0;i<n;i++)t1[i]=a[i];
for(int i=0;i<m;i++)t2[i]=b[i];
for(int i=n;i<lim;i++)t1[i]=0;
for(int i=m;i<lim;i++)t2[i]=0;
NTT(t1,1,lim),NTT(t2,1,lim);
for(int i=0;i<lim;i++)t3[i]=1ll*t1[i]*t2[i]%mod;
NTT(t3,-1,lim);
for(int i=0;i<n+m-1;i++)c[i]=t3[i];
}
namespace Evaluation{
#define ls(p) p<<1
#define rs(p) p<<1|1
int *T1[MAXN],*T2[MAXN],T3[MAXN],T4[MAXN],flow[MAXN*32],*now=flow;
void clear(){now=flow;}
inline void MUL2(int *a,int *b,int *c,int n,int m,int lim){
static int t1[MAXN],t2[MAXN],t3[MAXN];
for(int i=0;i<n;i++)t1[i]=a[i];
for(int i=0;i<m;i++)t2[i]=b[i];
reverse(t2,t2+m);
for(int i=n;i<lim;i++)t1[i]=0;
for(int i=m;i<lim;i++)t2[i]=0;
NTT(t1,1,lim),NTT(t2,1,lim);
for(int i=0;i<lim;i++)t3[i]=1ll*t1[i]*t2[i]%mod;
NTT(t3,-1,lim);
for(int i=m-1;i<n;i++)c[i-m+1]=t3[i];
}
void pre(int *Q,int p,int l,int r){
T1[p]=now,now+=r-l+2;
T2[p]=now,now+=r-l+2;
for(int i=0;i<=r-l+1;i++)T1[p][i]=T2[p][i]=0;
if(l==r){
T1[p][0]=1;
T1[p][1]=(mod-Q[l])%mod;
return ;
}
int mid=(l+r)>>1;
pre(Q,ls(p),l,mid);
pre(Q,rs(p),mid+1,r);
if(r-l+1<=256){
for(int i=0;i<=mid-l+1;i++)
for(int j=0;j<=r-mid;j++)
T1[p][i+j]=add(T1[p][i+j],1ll*T1[ls(p)][i]*T1[rs(p)][j]%mod);
}else{
int lim=init_NTT(r-l+1);
MUL(T1[ls(p)],T1[rs(p)],T1[p],mid-l+2,r-mid+1,lim);
}
}
void Solve(int *S,int p,int l,int r){
if(l==r){
S[l]=T2[p][0];
return ;
}
int mid=(l+r)>>1;
int lim=init_NTT(r-l+1);
MUL2(T2[p],T1[rs(p)],T2[ls(p)],r-l+1,r-mid+1,lim);
MUL2(T2[p],T1[ls(p)],T2[rs(p)],r-l+1,mid-l+2,lim);
Solve(S,ls(p),l,mid);
Solve(S,rs(p),mid+1,r);
}
//opt0/1 区分多点求值/快速插值
void evaluation(int *F,int *Q,int *S,int n,int m,int opt){
clear();
static int AF[MAXN];
n=max(n,m+1),m=max(m,n-1);
pre(Q,1,1,m);
if(opt){
for(int i=0;i<n;i++)AF[i]=T1[1][i];
reverse(AF,AF+n);
Polydao(AF,AF,n+1);
}
Polyinv(T1[1],T3,m+1);
reverse(T3,T3+m+1);
int lim=init_NTT(n+m+1);
if(!opt)MUL(F,T3,T4,n,m+1,lim);
else MUL(AF,T3,T4,n,m+1,lim);
for(int i=n;i<n+m;i++)T2[1][i-n]=T4[i];
Solve(S,1,1,m);
for(int i=1;i<=m;i++)S[i]=(1ll*S[i]*Q[i]%mod+(!opt?F[0]:AF[0]))%mod;
for(int i=0;i<=n+m+1;i++)T3[i]=T4[i]=0;
}
};
namespace Lagrange_Interpolation{
#define ls(p) p<<1
#define rs(p) p<<1|1
int S[MAXN],*T[MAXN],flow[MAXN*32],*now=flow,tmp1[MAXN],tmp2[MAXN],e1[MAXN],e2[MAXN];
void solve(int p,int l,int r){
T[p]=now,now+=r-l+2;
if(l==r){
T[p][0]=S[l];
return ;
}
int mid=(l+r)>>1;
solve(ls(p),l,mid);
solve(rs(p),mid+1,r);
for(int i=0;i<mid-l+1;i++)tmp1[i]=T[ls(p)][i];
for(int i=0;i<r-mid;i++)tmp2[i]=T[rs(p)][i];
for(int i=0;i<r-mid+1;i++)e1[i]=Evaluation::T1[rs(p)][i];
reverse(e1,e1+r-mid+1);
for(int i=0;i<mid-l+2;i++)e2[i]=Evaluation::T1[ls(p)][i];
reverse(e2,e2+mid-l+2);
int lim=init_NTT(r-l+1);
MUL(tmp1,e1,e1,mid-l+1,r-mid+1,lim);
MUL(tmp2,e2,e2,r-mid,mid-l+2,lim);
for(int i=0;i<=r-l;i++)T[p][i]=add(e1[i],e2[i]);
}
void Interpolation(int *x,int *y,int *ans,int n){
Evaluation::evaluation(x,x,S,n+1,n,1);
for(int i=1;i<=n;i++)S[i]=1ll*y[i]*qkpow(S[i],mod-2)%mod;
solve(1,1,n);
for(int i=0;i<n;i++)ans[i]=T[1][i];
}
}
void Pre(int P){
int invP=qkpow(P,mod-2),kk=0,bb=0;
K[0]=1,B[0]=0;
for(int i=1;i<=k+1;i++){
K[i]=1ll*K[i-1]*invP%mod;
B[i]=1ll*(B[i-1]+qkpow(i,k))*invP%mod;
int Num=C(k+1,i);
if(i&1)kk=dec(kk,1ll*Num*K[i]%mod),bb=dec(bb,1ll*Num*B[i]%mod);
else kk=add(kk,1ll*Num*K[i]%mod),bb=add(bb,1ll*Num*B[i]%mod);
}
kk=(kk+1),kk=(kk==mod?0:kk);
g[0]=1ll*(mod-bb)*qkpow(kk,mod-2)%mod;
for(int i=1;i<=k;i++)g[i]=add(1ll*g[0]*K[i]%mod,B[i]);
for(int i=1;i<=k+1;i++)x[i]=i-1,y[i]=(g[i-1]+mod)%mod;
Lagrange_Interpolation::Interpolation(x,y,F,k+1);
for(int i=0;i<=k;i++)F[i]=(F[i]+mod)%mod;
// cout<<endl;
for(int i=1;i<=n;i++)Q[i]=b[i];
Evaluation::evaluation(F,Q,val,k+1,n,0);
for(int i=1;i<=n;i++)val[i]=(val[i]+mod)%mod;
}
inline void makeit(int Id,int y,Matrix& S){
//[S1S2,S1,S2,product of b]
int X=dec(1ll*qkpow(P,y+1)*val[Id]%mod,1ll*P*g[0]%mod);
S.a[0][0]=add(y,1),S.a[1][0]=y,S.a[2][0]=X,S.a[3][0]=X;
S.a[1][1]=add(y,1),S.a[3][1]=X;
S.a[2][2]=add(y,1),S.a[3][2]=y;
S.a[3][3]=add(y,1);
}
signed main(){
gi(n),gi(k),gi(P);
init();
for(int i=1;i<=n;i++)gi(b[i]);
Pre(P);
for(int i=1;i<=n;i++)makeit(i,b[i],d[i]);
dp[1]=d[1];
for(int i=2;i<=n;i++)dp[i]=dp[i-1]*d[i]+d[i];
for(int i=1;i<=n;i++)ans+=dp[i];
pi(ans.a[3][0],'\n');
return 0;
}










Thanks for the fast editorial! <3
-- Excuse me, what is the worst problem did you solved ever? -- Cf #789 B2. -- (surprising)
Although the problem was a bit difficult, but just because you missed some observation does not mean that problem was bad.
Remember:
Typical cyan attitude.
B2 was not a bad problem though...
in div1D I thought that we choose k indices where we swap $$$p_i$$$ and $$$p_{i+1}$$$ (((
Certainly not the most comfortable round for Div2, but I liked problem C. Thanks for a great editorial btw.
Obligatory to say this, since many people are talking about it:
Div1A in $$$\mathcal O(n^2 \log n)$$$ (with a BIT/Fenwick Tree) fits within the time limit, even though I think $$$n \leq 5000$$$ was chosen to specifically cut out these solutions.
Yeah, that's straight up bad prep. Either they should have made a lower limit, or made these solutions fail.
Mine ordered set solution fails but others Fenwick tree solution passes that's a bit unfair
ordered_set is much slower than Fenwick
Then how to decide between Fenwick and ordered set
Always choose fenwick over ordered_set if you can use both
My Custom Implemented Order Statistics Passed in ~561 ms : https://codeforces.com/contest/1678/submission/156411337
Checkout my blog as well ;) -> Blog
ordered set does work, you might have been doing redundant operations https://codeforces.com/contest/1678/submission/156385249
Editorial mentions that n^2 logn solutions can pass too, so ig they didn't intend to cut them?
It is hard to cut them. Who use n^2 logn solutions also will lose time.
I'm a bit surprised since my n^2logn solution using only upper_bounds(which are probably faster than/ not much slower than BIT) got TLE.
Yeah, I also assumed that upper_bound should be faster
But now that I think about it rationally, BIT has much fewer operations, particularly by half fewer conditional jumps which are damn expensive. So it is only natural that bit is much faster
mine too got TLE ...
"was chosen to specifically cut out these solutions."
Well, what is the point of cutting logn solutions? It doesn't even make the general idea much different
Actually problem F can be solved when $$$k \leq 10^6$$$, my solution has complexity $$$O(k\log k + n\log^2 n)$$$.
Our goal is to compute the coefficient of some polynomial $$$S(n)$$$ satisfying
We have
Therefore we have
we write $$$S(x+1) = \mathrm{e}^{\mathrm D} S(x)$$$ formally, here $$$\mathrm D$$$ is the differential operator, then we have
thus
we only need to compute the multiplicative inverse of $$$p\mathrm{e}^x - 1$$$, which can be done in $$$O(k\log k)$$$.
Here's an alternative phrasing of this concept, which inlines the differential operator a little bit.
Fix a polynomial $$$A(x) = a_0 + a_1 x^1 + a_2 x^2 + \cdots + a_k x^k$$$. Now, let $$$t$$$ be a formal variable, and note that for any $$$n$$$, $$$e^{nt} = \sum_{i \ge 0} \frac{1}{i!} n^i t^i$$$. In particular, this contains all powers of $$$n$$$, so we multiply this by a polynomial to get linear combinations of powers of $$$n$$$ (i.e. polynomials). In particular,
Where $$$[t^k]$$$ denotes taking the coefficient of $$$t^k$$$. Let $$$\hat{A}(t) = k! a_k t^0 + (k-1)! a_{k-1} t^1 + \cdots + 0! a_0 t^k$$$, so that $$$A(n) = [t^k] \hat{A}(t) e^{nt}$$$.
Now, consider the sum $$$\sum_{i=0}^{n-1} p^i A(i)$$$. We can use the above form to get
(This is valid because $$$[t^k]$$$ is a linear operator.) Note that $$$\sum_{i=0}^{n-1} p^i e^{it}$$$ is a geometric sum! Thus, we get
We can split this term into
Note that this only depends on the first $$$k+1$$$ coefficients of $$$\hat{A}(t) / (pe^{t} - 1)$$$, and the left hand term can be viewed as a different polynomial evaluated at $$$n$$$. The rest of the solution is the same.
One final note: if $$$p = 1$$$, then $$$e^t - 1$$$ does not have a generating function inverse, as it has constant term $$$0$$$. In this case, we can instead use
since $(e^t-1)/t$ has nonzero constant term. The generating function $$$((e^t-1)/t)^{-1}$$$ is thus the key thing to compute to find sums of powers; this is in fact the EGF of the Bernoulli numbers.
ayy fast editorial :)
We can solve 1677A - Tokitsukaze and Strange Inequality in more straightforward manner. 156343295
This is actually very good solution, i understood it better than the editorial itself.
Sorry for being late, but can you please explain this solution?
It's quite late already, but let me try:
He's going through all possible A-C pairs by the 2 for loops and is storing B-D pairs count in DP.
ii = C; jj = A; dp[jj] = pairs of B-D for the current A(=jj);
if the number standing on index jj is less than on the number on ii, it means this pair is a valid A-C pair and he's adding all valid B-D pairs(=Cnt) for the current jj(=A). He has stored sum of all B-D pairs from ii down to jj(=from C down to A). Index A(=jj) isn't included, since he adds it after the summation.
'Cnt+=dp[jj]' adds all valid B-D pairs into the current sum(=Cnt) for this A-C. And then he increases dp[jj] IF the value aa[jj] is greater than aa[ii], which basically is 'if(a[b]>a[d])'. This line ensures we have correct amount of valid B-D pairs in the dp.
I hope this makes sense, although it's been quite a while since you asked.
This solution is extremally elegant, it's just so good and clever, haven't seen something like this for quite a while, wp.
Thanks for nice debugging template.
I'm very sorry for question 1F in div1. This question is not only the same as the question( https://judge.yosupo.jp/problem/sum_of_exponential_times_polynomial) (I haven't seen it before), but it's really a garbage question. I'm very sorry for affecting the experience of div1 participants. I won't have such a problem next time.
My English is a little poor and may not be smooth.
There is no need to say "something is garbage" because it has appeared before.
Personally, I didn't solve the libchecker task, and I do learn something new from the task (especially from the comment from Elegia). So I really appreciate the task.
On the other hand, I just don't quite like the "wrapping" part of task. Next time you can try to come up with something more interesting. :)
Thank you for your comments. I agree with you. If possible, I will try to think of something more interesting.
C was leaked on telegram. Link to the solution — https://ide.geeksforgeeks.org/cf163b70-3b16-4e83-a880-a9b2756fcf78. Please ban those who have cheated.
tokitsukaze MikeMirzayanov
dp states for problem B is wrong, please correct to
Solution link
Thank you for pointing out.
I did Problem C in O(n^2 logn) using binary search, got TLE. But the editorial says it will pass. How is this possible? My solution link : https://codeforces.com/contest/1678/submission/156353215
My solution is also O(n^2 logn) and it passes comfortably: I did it by brute-forcing b and c here
Well theoretically it should not pass as the # of operations: O(5000*5000*13) = 3.25 * 10^8. And we can process 10^8 operations in 1 sec.
You assumed it takes exactly 1e8 operations in a second. I've seen somewhere I can't remember that its something like 4e8 or so(not sure but i'm sure 1e8 is just used as a rough estimate)... Also, stuff like compiler optimizations etc might happen.
Function overhead + Higher constant?
If you prefer command line, checkout CF Doctor for more flexibility and faster feedback.
If you are/were getting a WA/RE verdict on problems from this contest, you can get the smallest possible counter example for your submission on cfstress.com. To do that, click on the relevant problem's link below, add your submission ID, and edit the table (or edit compressed parameters) to increase/decrease the constraints.
Divison 2
Divison 1
If you are not able to find a counter example even after changing the parameters, reply to this thread (only till the next 7 days), with links to your submission and ticket(s).
Hey! Getting the error "Constraints were violated." even with default values. Not sure what's wrong? Problem Div2D. Ticket 6965.
Hi codefforces I inspected the logs and your submission throws a compilation error when using C++17. (NOTE: C++20 support is officially not added yet).
(You can confirm this by clicking on "View Logs" in the ticket status page, there you won't find any line denoting "Found failing test", indicating an early failure.
I'll improve the error message shortly (and add C++20 support soon).
I temporarily enabled C++20 support, and ran your submission again. Here's the failing testcase: Ticket 6975
P.S: I know, I know. I also promised you another feature a couple of days back that I'm yet to work on. How come you're always the unlucky one to encounter these bugs? xD.
Got it, thanks. Hahaha I'm a chaos monkey by coincidence. Btw it's satisfaction seeing cfstress grow day by day. Like a tree. Cheers!
I think the most important observation for B1 & B2 is that we can just look at each digit-pair's index to determine whether we need to change it: specifically, if we have an "01" or "10" at an even position, we must change it, because finally every segment will be of even length so each such "01" or "10" must reside in a single segment instead of at the boundary of two segments.
Unfortunately I missed this observation during the contest and failed to solve B2... and solved B1 using a more complicated solution.
Thanks for the good round!!! Thanks for the editorial!!!
Why is it written in editorial that n*n*logn should pass in Div2C?
a problem can be solved by many methods,we should not think one problem only to one solution
But I got TLE on n*n*logn :(
May I have a look about your solution?
This 156351799 solution was getting TLE.
I read through your code and noticed that there are a lot of copy-like or sort-like parts in your code, which will greatly increase the running time of your code by a constant multiple (roughly counted as 6 times). $$$O(n^2logn)$$$ is not an optimal solution in the first place, and will probably fail in the case of large constants. But your idea is roughly correct, you can try to maintain the steps of the array sorting section to maintain the previous and next values through the value field by O(n^2), thus avoiding the log
Thanks for your reply. Got it!
by the wall , you can use int instead of ll except the final answer
https://paste.ubuntu.com/p/Z4mNJ6r2Rc/
this is my friend's code
For Div. 2 C, this solution can also pass. Let
suffix_count[i][v]be the number of elements inp[i..n]that is smaller thanv. Similarly we haveprefix_count[i][v]. Those two arrays can be calculated inO(n^2): first enumeratevthen enumerateiand maintain the suffix/prefix total. Then you just enumerate all1 < b < c < n, and for each pair ofbandcjust addsuffix_count[c + 1][p[b]] * prefix_count[b - 1][p[c]]to the answer.I implemented exactly this (but with different two iterations)
156328504
I read the first question wrong and wasted more than one hour in it. It feels frustrating :(
Wait till you encounter a contest where you spend one hour to finish reading what Petya is up to.
Why does 156322948 this solution pass and 156357149 gives MLE. Both have O(n2) space complexity I think.
Used int instead of long long and it passed ;_;
For me I was using array during contest it was showing MLE. But now with same size vector it passed
Today's Div2c is similar to click here
Can anyone explain more about the tutorial of div1 E? What's the difference algorithm and the a*R+b part?
Yeah I couldn't figure that out either, but here's an alternate solution.
First, for each $$$x \in [1, n]$$$, precalculate:
There are $$$O(n \log n)$$$ triples $$$(a, b, c)$$$ where $$$1 \le a < b \le c \le n$$$ and $$$a \cdot b = c$$$. For each such triple we can find their positions in $$$p$$$; if they are all in $$$c$$$'s active range, then there is some $$$l_1, l_2, r_1, r_2$$$ where all segments $$$[l, r]$$$ where $$$l \in [l_1, l_2]$$$ and $$$r \in [r_1, r_2]$$$ are beautiful. You can imagine a $$$n \times n$$$ grid of cells where the $$$x$$$ and $$$y$$$ axes represent $$$l$$$ and $$$r$$$ respectively; this would translate to marking a rectangular region of the cells. Then the answer for each query $$$[l, r]$$$ is the number of marked cells in the region $$$x \in [l, r]$$$ and $$$y \le r$$$. (It turns out for later analysis that it's easier to count unmarked cells and subtract it from the area of the region)
To speed this up, one might think of a 2D lazy segment tree with "region add" and "count zeros in region" (via minimum and frequency of minimum). But this is complicated, requiring an implicit storage strategy to cut down on space, and more importantly, may be too slow with total time complexity $$$O(n \log^3 n + q \log^2 n)$$$.
Instead, we use only a 1D lazy segment tree and do a sweep line over the $$$y$$$ axis. Region add becomes two range adds, one positive and one negative. To implement "count zeros in region", we solve the queries offline, at time $$$y = r_i$$$. But we also need to implement a "tick" operation when advancing $$$y$$$, whose basic description is "if range minimum is $$$0$$$, add its frequency to a historic sum $$$zeros$$$"
For a lazy segment tree to work, all possible range update operations, and compositions thereof, must be unified into a single small data structure that is cheap (preferably $$$O(1)$$$) to copy, compose, and apply, so we somehow need to summarize an arbitrary sequence of range adds and ticks into such a data structure.
Multiple range adds are easy, just add their deltas. Multiple ticks are also pretty easy, just store the number of ticks elapsed, then perform them all at once using multiplication. However, range adds and ticks do not commute with each other, so it's not sufficient to merely store these counts separately.
Turns out though, we only care about the ticks that happen when the range minimum is zero, and this can only happen when the delta (prefix sum of range adds) is at the minimum value. So any sequence of update operations can be summarized by a triple of values:
Final time complexity is $$$O(n \log^2 n + q \log n)$$$.
I have a similar solution 157331395 with the following differences:
When generating rectangles for $$$c$$$, we can do a small tweak so no two rectangles intersect with each other, this will make the count easier. We use $$$(x1, y1, x2, y2), x1 \le x2, y1 \le y2$$$ to represent a rectangle.
We do a sweep line over the $$$x$$$ axis, move $$$X$$$ from $$$1$$$ to $$$n$$$, we use two 1D segment trees:
$$$F$$$: Count the cover of rectangles that are fully inside the current region, i.e. the rectangle's $$$x2 \le X$$$. Let $$$F_y = $$$ the number of covered cells $$$(x, y), 1 \le x \le X$$$. We just use the traditional "range add, query sum" segment tree.
$$$G$$$: Count the cover of rectangles that are partially inside the current region, i.e. $$$x1 \le X \lt x2$$$. Each leaf node $$$G_y$$$ maintains:
1. $$$x$$$: $$$x1$$$ of the rectangle covering column $$$y$$$, or 0 if it is not covered.
2. $$$cnt$$$: 1 if column $$$y$$$ is covered, or 0 if it is not covered.
Non-leaf nodes maintain the sum of $$$x$$$ and sum of $$$cnt$$$. It is a modification of "range set, query sum" segment tree. We need to add an extra field to indicate if the column is covered.
For every rectangle whose $$$x1 = X$$$, add it to $$$G$$$. For every rectangle whose $$$x2 = X$$$, remove it from $$$G$$$ and add it to $$$F$$$.
To calculate the number of covered cells inside rectangle region (1, 1, X, Y): Let $$$g$$$ = $$$G$$$.query(1, $$$Y$$$). The count = $$$g$$$.$$$cnt * (X+1) - g$$$.$$$x + F$$$.query(1. $$$Y$$$)
There is an easier way to do so:
Let's say we want to find the "rectangles" for $$$p_i$$$. The active region of $$$p_i$$$ (maximal neighbourhood of $$$p_i$$$ having no number greater than itself) can be visualized as something like:
(Each pair of cells at positions $$$x$$$ and $$$y$$$ with same colors has $$$p_x.p_y = p_i$$$)
Let the active region of $$$p_i$$$ be $$$[L, R]$$$. Now notice that any valid (beautiful) range $$$[l, r] $$$which has its maximum as $$$p_i$$$ must have atleast one of these same color pairs completely within it. Now it's easy to see that any such maximal set of valid ranges having maximum as $$$p_i$$$ can also be generated if we completely ignore those pairs of colored cells which have another pair lying completely within them (for example in given image, yellow and blue can be removed).
So we can ignore such "colors", and finally we are left with a set of pairs (two cells with same color constitute a pair) in which for any two pairs $$$(l_i, r_i)$$$ and $$$(l_j, r_j)$$$ if $$$l_i < l_j$$$ then $$$r_i < r_j$$$.
The example shown above becomes:
Now we can divide such a region into a $$$O(colors)$$$-sized set $$$S$$$ of quartets $$$(l_1, r_1, l_2, r_2)$$$ such that for any beautiful range $$$[l, r]$$$ having maximum as $$$P_i$$$, there exists one and only one element in $$$S$$$ $$$(a, b, c, d)$$$ such that $$$a \leq l \leq b$$$ and $$$c \leq r \leq d$$$.
How to do so? Just sort the set of colored pairs by their first element. The quartet corresponding to the $$$i$$$'th colored pair is $$$(L, l_i, r_i, (r_{i + 1} - 1))$$$ (for last pair, $$$(r_{i + 1} - 1) = R$$$).
Our example becomes: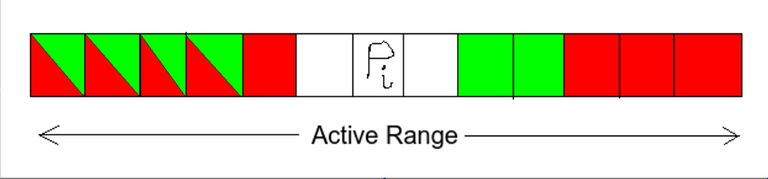
(for each color, a valid range is that which has left border in left group of some colored cells, and right border in right group of cells with same color)
Implementation: link
Hi can someone tell me why this code times out on Div2.C. I am new to segment trees but I knew there was a way to use it to find the number of elements less than x within a given range, so I took the code online and tried it but it times out. Any help is appreciated. Thank you https://codeforces.com/contest/1678/submission/156367158
I might be wrong but I think it is just because of constants. Segment tree already has very big constants and your implementation uses vectors which adds more constants and is not necessary. Try to use a Fenwick tree instead which is strictly O(logN).
you need O(n^2) to pass this problem.
Participating in div2 contest was pretty hard for me because of B2 being so strange. Anyway, I upsolved this contest and I have 1 question: How D2F (D1D) is supposed to be D2F? It seems pretty like D2D for me, and I spent much more time on D2D/D2E, than on D2F
Can someone please help me understand what the variable y means in the greedy solution for problem B2? I've been trying to wrap my head around the greedy solution, but I'm just not getting it.
sjfsb
I cannot understand why I have to check if it is impossible to make original permutations in div1 D. In statement, you said that the unclear value sequence was originated from some value sequence that Tokitsukaze made. So I think the unclear value sequence of the problem must have at least one correct original permutation.
Div-2 C is kind of hard to understand from the tutorial. Anyone else having problem too?
div-2, Problem B, this problem is an example of how valuable a good observation is!
Problem E $$$2c * (N - c)$$$ is obtained from the following: We choose the largest $$$c$$$ numbers from 1 ~ N with positive contribution and smallest $$$c$$$ numbers from 1 ~ N with negative contribution. The answer is twice the sum.
$$$2 * [-(1 + 2 + ... + c) + (N - c + 1) + (N - c + 2) + ... + N]$$$
$$$= 2 * [-(c + 1) * c / 2 + (2 * N - c + 1) * c / 2]$$$
$$$= c * (2 * N - 2 * c)$$$
$$$= 2c * (N - c)$$$
In div1. C, can someone give formal proof for why alternating between maximum and minimum, maximizes the beauty?
Could't solve B2. It seems like a greedy problem but instead it's dp, and I didn't even think of dp:(
Can anyone explain how was the below formula in the problem Tokitsukaze and Two Colorful Tapes Div 1 C derived:
c=∑⌊CircleSize / 2⌋, N represents the size of the permutation, score=2c⋅(N−c).
I understood the part of valleys and peaks. But I can not seem to connect that with this formula which is said to be derived from the summation formula of the arithmetic sequence.
So I finally found out how we can get the score value from the summation formula of the arithmetic sequence. Here if we consider all the cycles then it will be a series of positive peak values and a series of negative valley values. So we need to take the highest peak with the lowest valley. So it would be like this:
(2*h_maxpeak — 2* h_minvalley),(2*h(maxpeak-1) — 2*h_(minvalley+1)),...._
This is how the series will go. If we have odd cycles then the last terms will get reduced. So if we consider n=10. This is how the series will go:
(Sorry for picture . I am not that adept yet to write equations in spoiler. Any help or resource on how to write equations in codeforces will be appreciated)
Please feel free to correct me if I have made any mistakes
bro I did not get it.Can u pls tell me again?
in question B1 can someone explain me this test case 110011000
your test case is wrong since n is guaranteed to be even and len(110011000)=9 which is odd ,read the problem again.
For div1 B I need help understanding the part of the tutorial about the rows
I tried doing div2 C with segment tree in n^2logn, but it tle's 157247666
Ladies and gentlemen, we got him!
I'm talking about div1F: the coefficients don't need to be interpolated, we have a direct (but not closed-form) formula.
Consider the Mellin operator $$$\mathsf{O} = x \frac{\mathrm{d}}{\mathrm{d}x}$$$. We want to find $$$h_{k,n} = \mathsf{O}^k \frac{Px-(Px)^{n+1}}{1-Px}$$$ for $$$x=1$$$ (yes, starting the sum from $$$1$$$ even for $$$k=0$$$). This operator follows the general Leibniz rule:
with proof by induction: it follows the Leibniz rule trivially for $k=0$ and
We need to express $D_k = \left. \mathsf{O}^k Px (1-Px)^{-1} \right|_{x=1}$. Ansatz $$$D_k = f_k(x) (1-Px)^{-k-1}$$$ gives a recurrence
which together with $f_0(x)=Px$ says $$$f_k$$$ is a polynomial with degree $$$k+1$$$ (proof by induction); denoting its coefficients by $$$f_{k,j} P^j$$$, we have
which is the formula for Eulerian numbers (shifted so indices start at $1$ and $$$f_{k,0}=0$$$). In short, $$$D_k = P A_k(P) (1-P)^{-k-1}$$$ where $$$A_k(x)$$$ is the $$$k$$$-th Eulerian polynomial. Btw, this is in Wikipedia too (with a mistake, unsurprisingly for Wikipedia).
How do we calculate $A_k(P)$ for $$$k \le K$$$? Eulerian polynomials have been studied extensively. We can use the formula $$$A_k(P) - \sum_{j\lt k} {k \choose j} A_j(P) (P-1)^{k-1-j} = 0$$$ for $$$k \gt 0$$$, which can be rewritten to
and this gives us a way to express the generating function $G(y) = \sum_k \frac{A_k(P)y^k}{k!(1-P)^{k+1}}$ as
so all we need to do is invert a polynomial.
Next, we can define a generating function of $h_{k,n}/k!$ for fixed $$$n$$$:
so what we're looking for is the $K$-th coefficient (multiplied by $$$K!$$$) of $$$\frac{1}{e^{-z}-P}\sum C_i (P-P^{n_i+1}e^{n_iz})$$$ where $$$C_i$$$ are the coefficients mentioned at the start of the editorial and computed in $$$O(N)$$$. I don't think this can be computed easily, multipoint evaluation seems better — but at least we got rid of interpolation.
For problem 1677A my submission has O(n^2) time complexity but it receives a TLE. Can anyone explain why?
you code complexity is O(n^4) not O(n^2) as you run nested loop on the two vectors which they contain O(n^2) elements so total complexity is O(n^4) ,try another approach.
Thanks!
can someone explain me the answer for rows in the problem 1677B — Tokitsukaze and Meeting
whoever wrote the editorial for div1c Tokitsukaze and Two Colorful Tapes is really a terrible writer
I didnt get the dp solution in b2 especially how did he got the cost calculating formula , can somebody help
``mySubmission
Thanks for the Chinese version of the tutorial.
I thought of a weird solution for C but it uses 3 ordered sets... The names a,b,c,d refers to indices in sync with the context of the question. I maintain an ordered set that initially contains all the elements but as we keep on erasing all the elements till the index c (as c moves forward) this set then represents the potential candidates for d since we can just use order of key for element(b) and get to know the number of possible options for this current b...
Now, at the same time we have an 'a' as well that is behind b (think of 2 for loops one decides b and the other decides c). Also, the elements in (b,c] are to be kept in another ordered set and [0,b) are to be kept in another ordered set and similarly use find by order for current ele(c) on the ordered set that contains ele in range [0,b). Deciding b and c using for loops is O(n^2) while find by order and similar operations take o(logn). Would this TLE???