Problem source: (Codedrift June, Interviewbit)
Given an integer array X with size A. Initially all the elements of this array are 0. Given another integer array Y with the same size A, all the elements here are also 0. You have to handle three types of queries:
1 L R — Flip all elements from 0 to 1 and 1 to 0 in range L to R (inclusive) in array X
2 P — For every element i in [1, A], do: Y[i] += X[i] * P
3 J — Find Y[j]
A <= 10^5 and Q <= 10^5
Would really be great if you could provide approach or hint. Contest is over. Here's the link to contest.











The problem is very similar to this.
It is not over yet.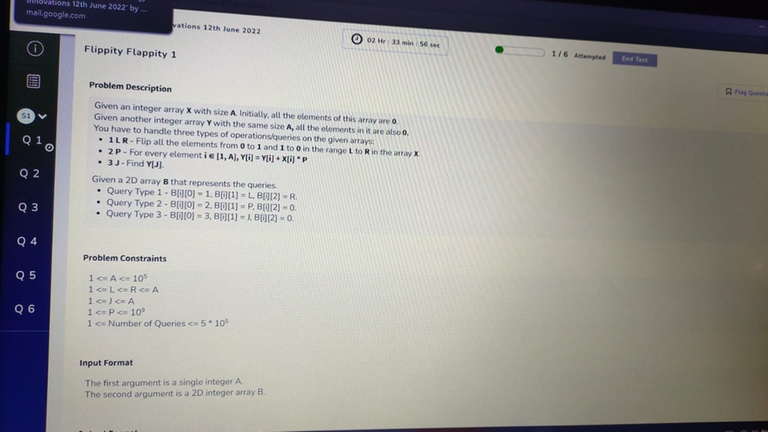
which company?
I didn't know either. I just got the screenshot from some blog.
Btw I had done this question today in leetcode by lazy propagation. Here is the link,https://leetcode.com/submissions/detail/1000924968/