How to use segment tree?
Build tree and query
You can read this aritical to learn some basic operations of segment tree.
Update and "Lazy Tag"
Lazy Tag
"Lazy Tag" is the most important part in updation. This method can reduce the time complexity to $$$O(\log(n))$$$ for each updation. It's obvious that we can't update the whole tree, or the time complexity will be $$$O(n)$$$ like build tree. To reduce the time complexity, if a segment is not queried now, we don't have to update it at present. We usually give it a tag to record how we update it. For example, if we want to update an array and query the sum of an interval, for each "add" operation, we do not add numbers to each segment, we only have to give a "add tag" to the some segments.

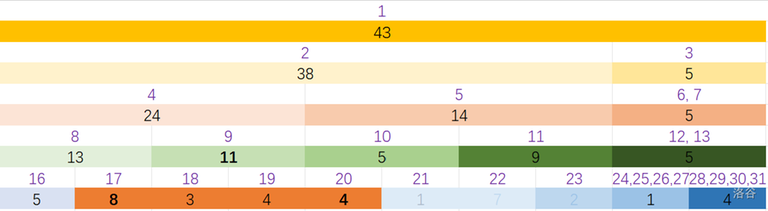
For example, if we want to add $$$2$$$ from $$$2$$$ to $$$5$$$. We should give segment number $$$9$$$, $$$17$$$ and $$$20$$$ an "add tag" to sign them.
Note that segment we signed are all a part of the interval we operate on.
This picture shows what the tree is like after the operation.
void change(int o, int l, int r)
{
if (ql <= l && r <= qr)
{
apply_add_tag(o, l, r, qv);
return;
}
push_down(o, l, r);
int mid = (l + r) >> 1;
if (ql <= mid) change(ls, l, mid);
if (mid < qr) change(rs, mid + 1, r);
// just like what we do in query
sum[o] = sum[ls] + sum[rs];
// push up the sum of the segment
}
if (ql <= l && r <= qr)
{
apply_add_tag(o, l, r, qv);
return;
}
This means if the segment is contain in the interval, we don't have to visit its sons because when we query we can push up this segment directly without ask the sons. This is the reson why we can operate on it and return.
void apply_add_tag(int o, int l, int r, ll v)
{
sum[o] += (ll)(r - l + 1) * v;
add[o] += v;
}
sum[o] += (ll)(r - l + 1) * v; This means the real value the segment should add = the value each node add * the length of the segment.
Push Down
When we query the segment which has a tag. We should update it. (of course we don't have to use extra time, we can update this when we query / update a new interval.
void push_down(int o, int l, int r)
{
if (add[o] != 0)
{
int mid = (l + r) >> 1;
apply_add_tag(ls, l, mid, add[o]);
apply_add_tag(rs, mid + 1, r, add[o]);
add[o] = 0;
}
}
add[o] = 0; Node that we have to clear the tag on the father segment after we push the tag down.
Someone may ask " when we clear the tag, how can we know know the real value of the segment?"
Don't forget that there is a push up operation when we update
sum[o] = sum[ls] + sum[rs];and there is a push down operation when we query.










