Problem statement
There is a kind of problems which want you to calculate the distant of the shortest path from some verdicts to other verdicts. This kind of problems are called "shortest path" in graph.
For example, in this graph, the distant of shortest path from verdict $$$1$$$ to verdict $$$6$$$ is $$$6$$$. And the distant of the shortest path from verdict $$$1$$$ to verdict $$$4$$$ is $$$5$$$.
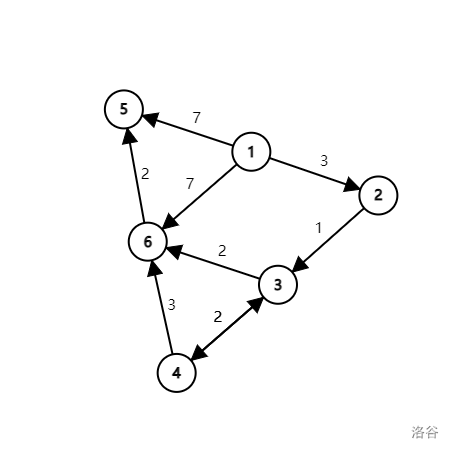
Specifically, there are $$$2$$$ of subproblems in shortest path:
Single sourse (one start point)
Multi source (multi start point)
Dijkstra and shortest path with single sourse
In shortest path with single sourse, we should calculate the distant of the shortest path from one verdict (Lets suppose the sourse is verduct $$$1$$$) to others. Dijkstra is the most common algorithm to solve this sort of problems.
Node that Dijkstra can only solve the problems with nonnegtive edge weight. For graphs with negtive edge weight, you can only use Bellman Ford.
Dijkstra is a kind of greedy. In each turn, We select the verdict with the shortest distance from the sourse and get the shortest path to it. After that we update the distant from the sourse to other verdict.
Lets look at the example:

| node | distant to the sourse(now) | shortest path |
|---|---|---|
| $$$1$$$ | \ | $$$0$$$ |
| $$$2$$$ | $$$3$$$ | \ |
| $$$3$$$ | \ | \ |
| $$$4$$$ | \ | \ |
| $$$5$$$ | $$$7$$$ | \ |
| $$$6$$$ | $$$7$$$ | \ |
Get the distant of the shortest path to verdict $$$2$$$.
| node | distant to the sourse(now) | shortest path |
|---|---|---|
| $$$1$$$ | \ | $$$0$$$ |
| $$$2$$$ | \ | $$$3$$$ |
| $$$3$$$ | $$$1+3=4$$$ | \ |
| $$$4$$$ | \ | \ |
| $$$5$$$ | $$$7$$$ | \ |
| $$$6$$$ | $$$7$$$ | \ |
Get the distant of the shortest path to verdict $$$3$$$.
| node | distant to the sourse(now) | shortest path |
|---|---|---|
| $$$1$$$ | \ | $$$0$$$ |
| $$$2$$$ | \ | $$$3$$$ |
| $$$3$$$ | \ | $$$4$$$ |
| $$$4$$$ | $$$6$$$ | \ |
| $$$5$$$ | $$$7$$$ | \ |
| $$$6$$$ | $$$6$$$ | \ |
Get the distant of the shortest path to verdict $$$4$$$ and verdict $$$6$$$.
| node | distant to the sourse(now) | shortest path |
|---|---|---|
| $$$1$$$ | \ | $$$0$$$ |
| $$$2$$$ | \ | $$$3$$$ |
| $$$3$$$ | \ | $$$4$$$ |
| $$$4$$$ | \ | $$$6$$$ |
| $$$5$$$ | $$$7$$$ | \ |
| $$$6$$$ | \ | $$$6$$$ |
Get the distant of the shortest path to verdict $$$4$$$ and verdict $$$6$$$.
| node | distant to the sourse(now) | shortest path |
|---|---|---|
| $$$1$$$ | \ | $$$0$$$ |
| $$$2$$$ | \ | $$$3$$$ |
| $$$3$$$ | \ | $$$4$$$ |
| $$$4$$$ | \ | $$$6$$$ |
| $$$5$$$ | \ | $$$7$$$ |
| $$$6$$$ | \ | $$$6$$$ |
Get the distant of the shortest path to verdict $$$7$$$.
The way Dijkstra is just like Prim (an algorithm of MST), we find the nearest verdict and them update the distant to other verdict.
Code: Dijkstra without heap, time complexity $$$O(n^2)$$$:
void dijkstra()
{
int node;
for (int i = 1; i <= n; ++i)
{
node = -1;
for (int j = 1; j <= n; ++j)
{
if (!vis[j] && (node == -1 || dis[j] < dis[node]))
node = j;
}
vis[node] = 1;
for (int j = 1; j <= n; ++j)
dis[j] = min(dis[j], dis[node] + g[node][j]);
}
}
Code Dijkstra with heap, time complexity $$$O(m\log(n))$$$:
void dijkstra()
{
dis[s] = 0;
Q.push((node){0, s});
while (!Q.empty())
{
node now = Q.top();
Q.pop();
int npos = now.pos, ndis = now.dis;
if (vis[npos] == false)
{
vis[npos] = true;
for (re int i = head[npos]; i != 0; i = e[i].next)
{
int to_pos = e[i].to;
if (dis[to_pos] > dis[npos] + e[i].dis)
{
dis[to_pos] = dis[npos] + e[i].dis;
if (vis[to_pos] == false)
Q.push((node){dis[to_pos], to_pos});
}
}
}
}
}










