hi everyone! my first post
Problem: a wooden rod is separated into pieces of length L1, L2, ..., Ln. Cutting a rod of length L into two pieces costs L. But we want to cut the rod into n-1 pieces. There is an optimal order of cuts that produces the minimum cost. (can be calculated by dynamic programming)
Is the minimum cost always smallest when the pieces are in order from smallest to greatest? I think it is, but do not know how to prove.











No. If we can rearrange pieces arbitrary (and I read from your last question that it is), than the optimal configuration can be reached with Huffman tree. Let's solve problem in reverse: we have pieces with length L1 .. Ln and we want to bring them together in any order paying La + Lb for connecting segments with lengths La and Lb.
It can be proved that the optimal algorithm is the following: select two minimal pieces (two arbitrary ones if many minimums exist) and connect them together. Furthermore, this is the only optimal algorithm.
The following example shows that it is not always possible to connect rods and leave them sorted.
after the second step we should connect (3 3) and 7, but they are separated by 4 and 5 and the order is broken.
what if u combine the connected pieces to get the sum, and sort at each stage? then it will look like this.
3 7 4 3 5, sort and get3 3 4 5 76 9 7, sort and get6 7 913 9, sort and get9 1322, single piece so not possible to combine furtherand answer will be sum of numbers at each stage,
(6+9) + (13) + (22) = 50.EDIT: complexity analysis below.
overall: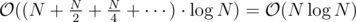
Yes, you can sort them at each stage, but after this operation original pieces won't be sorted.
6 7 9is3 3 7 4 5in original order, and, obviously, this is not a sorted array :)Are you saying that after the sort, you combine element x with element x+1 (for even x)? If so, I think this is wrong.
For the input {1, 2, 100, 101}, your algorithm would give 408, while the correct answer is 313.
Your algorithm's pairings: ((1 2) (100 101))
Correct pairings: (((1 2) 100) 101)
No, he's not saying that. UTFG on Huffman code for more.
He's saying that after the sort, we combine elements 1 and 2. No more than that. You're just misunderstanding ifsmirnov's example notation — braces denote already merged pieces; he just didn't write the pieces in sorted order. For your example, it's
for his, it's
I've read about Huffman codes, no need to be rude.
Did you read the edit in JuanMata's comment ("complexity analysis below")? If you sort all segments in each step, complexity is O(N^2 log N). However, he said that complexity is O(N log N). Furthermore, he says that the second step takes O(N/2 log (N/2)) time, indicating that each step in his algorithm reduces N to N/2. Your interpretation would reduce N to N-1, which doesn't seem to be what he intended.
Obviously this can be sped up by using a priority queue, but that's not really what's being commented on here. I was simply correcting JuanMata's algorithm.
I wasn't being rude (at least not from the point of view I'm used to), just direct :D
Oh. Sorry then. I assumed that the replies were transitive in this case, and it kind of made sense for me there.
OK, no offense taken, I may have misinterpreted your response.
Xellos tried to be very confusing below, so now i think its my turn! :D
i wrongly interpreted ifsmirnov's correct approach, and ended up giving a wrong solution. then aquamongoose correctly interpreted my wrong interpretation of ifsmirnov, and corrected my solution. later Xellos wrongly interpreted aquamongoose (thinking that i correctly interpreted ifsmirnov and that aquamongoose wrongly interpreted me), but ended up giving the same solution as both of us.
is it too confusing? if not, is it atleast more confusing than Xellos's comment? :D
finally after all the confusion due to wrong interpretations (not to mention comments like this! :P), luckily we have all come to a consensus about the final solution, which i have posted below.
i misinterpreted ifsmirnov's approach, and so my previous comment is wrong (as shown by aquamongoose above).
the correct solution (what ifsmirnov really meant) is to find the minimum two numbers at each stage, and combine only these two into their sum.
for the same example as above, the array at each stage would look like:
3 3 4 5 7(input)6 4 5 76 9 713 922therefore minimum answer is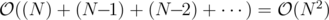
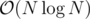 using Xellos's suggestion to use a
using Xellos's suggestion to use a
6+9+13+22 = 50.complexity:
EDIT: complexity can be bettered to
maporpriority_queueto store the values.As shown by my comment which is right, aquamongoose's comment which disproved ifsmirnov's comment is wrong, so ifsmirnov's comment and you comment which responded to that one are right. And this comment is right, but not because it's according to aquamongoose's comment, but because it just says the same as everyone. Is it confusing enough, or should I try more? :D
Also to the complexity: Use the
set<>, Luke! What you're doing is removing 2 elements from the set and adding their sum. There's no need for O(N2) here.Set is bad, set doesn't allow equal elements to be in it. Use multiset or priority_queue, which suits perfectly to such kind of tasks.
Details. That was not my point.
try to confuse more :D