Please note that this blog is a review of this problem. It is not novel enough to be an editorial. This problem may not be difficult for those people who are beyond purple, but very difficult for me.
To be more self-contained, I copy the problem here:
Problem Statement:
You are given strings $$$S$$$ and $$$T$$$ of length $$$n$$$ each, consisting of lowercase English letters.
For a string $$$X$$$ and an integer $$$i$$$, let $$$f(X,i)$$$ be the string obtained by performing on $$$X$$$ the following operation $$$i$$$ times:
Remove the first character of $$$X$$$ and append the same character to the end of $$$X$$$.
Find the number of integer pairs $$$(i,j)$$$ satisfying $$$0≤i,j≤n−1$$$ such that $$$f(S,i) \leq f(T,j)$$$ lexicographically.
For example, when $$$n=3$$$, $$$S=$$$"adb", $$$T=$$$"cab", there are 4 pairs: (1)$$$i=j=0$$$, "adb" $$$\leq$$$ "cab"; (2)$$$i=2, j=0$$$, "bad" $$$\leq$$$ "cab"; (3)$$$i=0, j=2$$$, "adb" $$$\leq$$$ "bca"; (4)$$$i=j=2$$$, "bad" $$$\leq$$$ "bca". You can find more test cases here: https://atcoder.jp/contests/abc272/tasks/abc272_f.
Here the problem statement ends. Now we analyze this problem.
The operation $$$f$$$ is a cyclic shift (CS). String concatenation is a powerful tool to handle string CS, eg, for $$$i=2$$$, $f(S, 2)$= "bad" is a substring of "adbadb". The string concatenation gets rid of mod operation to find index after CS, since mod operation is quite difficult to handle.
Let $$$S2=S+S$$$, $$$T2=T+T$$$. Here we want to count the pair $$$(i, j)$$$ such that $$$S2.substr(i, n) \leq T2.substr(j, n)$$$. But this is $$$O(n^3)$$$. So here we need another tool: suffix array. Suffix array sorts the suffix of a string. For example, the suffix array of "baad" is $$$\{1, 2, 0, 3\}$$$, because the lexicographic order (from small to big) is: ("aad" $$$1$$$, "ad" $$$2$$$, "baad" $$$0$$$, "d" $$$3$$$). Please note that the SA-IS algorithm could compute suffix array efficiently enough in O(Length of String). Here is the example code, you may find a C++ implementation of SA-IS in Ac-library:
#include <bits/stdc++.h>
using namespace std;
template<typename T, T...>
struct myinteger_sequence { };
template<typename T, typename S1 = void, typename S2 = void>
struct helper{
std::string operator()(const T& s){
return std::string(s);
}
};
template<typename T>
struct helper<T, decltype((void)std::to_string(std::declval<T>())), typename std::enable_if<!std::is_same<typename std::decay<T>::type, char>::value, void>::type>{
std::string operator()(const T& s){
return std::to_string(s);
}
};
template<typename T>
struct helper<T, void, typename std::enable_if<std::is_same<typename std::decay<T>::type, char>::value, void>::type>{
std::string operator()(const T& s){
return std::string(1, s);
}
};
template<typename T, typename S1 =void, typename S2 =void>
struct seqhelper{
const static bool seq = false;
};
template<typename T>
struct seqhelper<T, decltype((void)(std::declval<T>().begin())), decltype((void)(std::declval<T>().end()))>{
const static bool seq = !(std::is_same<typename std::decay<T>::type, std::string>::value);
};
template<std::size_t N, std::size_t... I>
struct gen_indices : gen_indices<(N - 1), (N - 1), I...> { };
template<std::size_t... I>
struct gen_indices<0, I...> : myinteger_sequence<std::size_t, I...> { };
template<typename T, typename REDUNDANT = void>
struct converter{
template<typename H>
std::string& to_string_impl(std::string& s, H&& h)
{
using std::to_string;
s += converter<H>().convert(std::forward<H>(h));
return s;
}
template<typename H, typename... T1>
std::string& to_string_impl(std::string& s, H&& h, T1&&... t)
{
using std::to_string;
s += converter<H>().convert(std::forward<H>(h)) + ", ";
return to_string_impl(s, std::forward<T1>(t)...);
}
template<typename... T1, std::size_t... I>
std::string mystring(const std::tuple<T1...>& tup, myinteger_sequence<std::size_t, I...>)
{
std::string result;
to_string_impl(result, std::get<I>(tup)...);
return result;
}
template<typename... S>
std::string mystring(const std::tuple<S...>& tup)
{
return mystring(tup, gen_indices<sizeof...(S)>{});
}
template<typename S=T>
std::string convert(const S& x){
return helper<S>()(x);
}
template<typename... S>
std::string convert(const std::tuple<S...>& tup){
std::string res = std::move(mystring(tup));
res = "{" + res + "}";
return res;
}
template<typename S1, typename S2>
std::string convert(const std::pair<S1, S2>& x){
return "{" + converter<S1>().convert(x.first) + ", " + converter<S2>().convert(x.second) + "}";
}
};
template<typename T>
struct converter<T, typename std::enable_if<seqhelper<T>::seq, void>::type>{
template<typename S=T>
std::string convert(const S& x){
int len = 0;
std::string ans = "{";
for(auto it = x.begin(); it != x.end(); ++it){
ans += move(converter<typename S::value_type>().convert(*it)) + ", ";
++len;
}
if(len == 0) return "{[EMPTY]}";
ans.pop_back(), ans.pop_back();
return ans + "}";
}
};
template<typename T>
std::string luangao(const T& x){
return converter<T>().convert(x);
}
namespace atcoder {
namespace internal {
std::vector<int> sa_naive(const std::vector<int>& s) {
int n = int(s.size());
std::vector<int> sa(n);
std::iota(sa.begin(), sa.end(), 0);
std::sort(sa.begin(), sa.end(), [&](int l, int r) {
if (l == r) return false;
while (l < n && r < n) {
if (s[l] != s[r]) return s[l] < s[r];
l++;
r++;
}
return l == n;
});
return sa;
}
std::vector<int> sa_doubling(const std::vector<int>& s) {
int n = int(s.size());
std::vector<int> sa(n), rnk = s, tmp(n);
std::iota(sa.begin(), sa.end(), 0);
for (int k = 1; k < n; k *= 2) {
auto cmp = [&](int x, int y) {
if (rnk[x] != rnk[y]) return rnk[x] < rnk[y];
int rx = x + k < n ? rnk[x + k] : -1;
int ry = y + k < n ? rnk[y + k] : -1;
return rx < ry;
};
std::sort(sa.begin(), sa.end(), cmp);
tmp[sa[0]] = 0;
for (int i = 1; i < n; i++) {
tmp[sa[i]] = tmp[sa[i - 1]] + (cmp(sa[i - 1], sa[i]) ? 1 : 0);
}
std::swap(tmp, rnk);
}
return sa;
}
// SA-IS, linear-time suffix array construction
// Reference:
// G. Nong, S. Zhang, and W. H. Chan,
// Two Efficient Algorithms for Linear Time Suffix Array Construction
template <int THRESHOLD_NAIVE = 10, int THRESHOLD_DOUBLING = 40>
std::vector<int> sa_is(const std::vector<int>& s, int upper) {
int n = int(s.size());
if (n == 0) return {};
if (n == 1) return {0};
if (n == 2) {
if (s[0] < s[1]) {
return {0, 1};
} else {
return {1, 0};
}
}
if (n < THRESHOLD_NAIVE) {
return sa_naive(s);
}
if (n < THRESHOLD_DOUBLING) {
return sa_doubling(s);
}
std::vector<int> sa(n);
std::vector<bool> ls(n);
for (int i = n - 2; i >= 0; i--) {
ls[i] = (s[i] == s[i + 1]) ? ls[i + 1] : (s[i] < s[i + 1]);
}
std::vector<int> sum_l(upper + 1), sum_s(upper + 1);
for (int i = 0; i < n; i++) {
if (!ls[i]) {
sum_s[s[i]]++;
} else {
sum_l[s[i] + 1]++;
}
}
for (int i = 0; i <= upper; i++) {
sum_s[i] += sum_l[i];
if (i < upper) sum_l[i + 1] += sum_s[i];
}
auto induce = [&](const std::vector<int>& lms) {
std::fill(sa.begin(), sa.end(), -1);
std::vector<int> buf(upper + 1);
std::copy(sum_s.begin(), sum_s.end(), buf.begin());
for (auto d : lms) {
if (d == n) continue;
sa[buf[s[d]]++] = d;
}
std::copy(sum_l.begin(), sum_l.end(), buf.begin());
sa[buf[s[n - 1]]++] = n - 1;
for (int i = 0; i < n; i++) {
int v = sa[i];
if (v >= 1 && !ls[v - 1]) {
sa[buf[s[v - 1]]++] = v - 1;
}
}
std::copy(sum_l.begin(), sum_l.end(), buf.begin());
for (int i = n - 1; i >= 0; i--) {
int v = sa[i];
if (v >= 1 && ls[v - 1]) {
sa[--buf[s[v - 1] + 1]] = v - 1;
}
}
};
std::vector<int> lms_map(n + 1, -1);
int m = 0;
for (int i = 1; i < n; i++) {
if (!ls[i - 1] && ls[i]) {
lms_map[i] = m++;
}
}
std::vector<int> lms;
lms.reserve(m);
for (int i = 1; i < n; i++) {
if (!ls[i - 1] && ls[i]) {
lms.push_back(i);
}
}
induce(lms);
if (m) {
std::vector<int> sorted_lms;
sorted_lms.reserve(m);
for (int v : sa) {
if (lms_map[v] != -1) sorted_lms.push_back(v);
}
std::vector<int> rec_s(m);
int rec_upper = 0;
rec_s[lms_map[sorted_lms[0]]] = 0;
for (int i = 1; i < m; i++) {
int l = sorted_lms[i - 1], r = sorted_lms[i];
int end_l = (lms_map[l] + 1 < m) ? lms[lms_map[l] + 1] : n;
int end_r = (lms_map[r] + 1 < m) ? lms[lms_map[r] + 1] : n;
bool same = true;
if (end_l - l != end_r - r) {
same = false;
} else {
while (l < end_l) {
if (s[l] != s[r]) {
break;
}
l++;
r++;
}
if (l == n || s[l] != s[r]) same = false;
}
if (!same) rec_upper++;
rec_s[lms_map[sorted_lms[i]]] = rec_upper;
}
auto rec_sa =
sa_is<THRESHOLD_NAIVE, THRESHOLD_DOUBLING>(rec_s, rec_upper);
for (int i = 0; i < m; i++) {
sorted_lms[i] = lms[rec_sa[i]];
}
induce(sorted_lms);
}
return sa;
}
} // namespace internal
std::vector<int> suffix_array(const std::vector<int>& s, int upper) {
assert(0 <= upper);
for (int d : s) {
assert(0 <= d && d <= upper);
}
auto sa = internal::sa_is(s, upper);
return sa;
}
template <class T> std::vector<int> suffix_array(const std::vector<T>& s) {
int n = int(s.size());
std::vector<int> idx(n);
iota(idx.begin(), idx.end(), 0);
sort(idx.begin(), idx.end(), [&](int l, int r) { return s[l] < s[r]; });
std::vector<int> s2(n);
int now = 0;
for (int i = 0; i < n; i++) {
if (i && s[idx[i - 1]] != s[idx[i]]) now++;
s2[idx[i]] = now;
}
return internal::sa_is(s2, now);
}
std::vector<int> suffix_array(const std::string& s) {
int n = int(s.size());
std::vector<int> s2(n);
for (int i = 0; i < n; i++) {
s2[i] = s[i];
}
return internal::sa_is(s2, 255);
}
} // namespace atcoder
int main(){
vector<int> v = move(atcoder::suffix_array("baad"));
cout << luangao(v) << "\n"; //{1, 2, 0, 3}
}
Let $$$Sf(S, i)$$$ be the suffix of S from index $$$i$$$ ($$$0$$$-indexed). For example, $$$Sf$$$("abcd", 1) = "bcd". The key idea is making a transform $$$g$$$ of $$$S, T$$$, together with their indices, such that $$$S2.substr(i, n) \leq T2.substr(j, n) \leftrightarrow Sf(g(S2, T2), g(i)) < Sf(g(S2, T2), g(j))$$$, where $$$g(S2, T2)$$$ is a large string obtained from $$$S2, T2$$$, and $$$g(i), g(j)$$$ are the transformed indices (because $$$i, j$$$ correspond to other indices different from $$$i, j$$$ in the large string $$$g(S2, T2)$$$). We need to transform the comparison of substrings to the comparison of suffices, by doing so we can utilize the powerful tool: SA-IS. Please note that there are never two equal suffices of a string because of different lengths.
One failed construction is $$$g(S2, T2) := T2 + S2$$$. For example, $$$T=$$$"zabf", $$$T2=$$$"zabfzabf", $$$S=$$$"abfz", $$$S2=$$$"abfzabfz", T2+S2="zabfzabfabfzabfz". One can check that, the suffix corresponding to the first "abf" ("abfzabfabfzabfz") < the suffix corresponding to the second "abf" ("abfzabfz").
Let's review the reason for the failure of our aforementioned construction. First, $$$Sf(T2+S2, i+2n) < Sf(T2+S2, j) \rightarrow S2.substr(i, n) \leq T2.substr(j, n)$$$ is obviously correct. If $$$S2.substr(i, n) < T2.substr(j, n)$$$, then $$$Sf(T2+S2, i+2n) < Sf(T2+S2, j)$$$. The problem occurs when $$$S2.substr(i, n) = T2.substr(j, n)$$$. We can imagine there are two pointers $$$p, q$$$ whose initial places are $$$i+2n, j$$$, respectively. Pointer $$$p, q$$$ go simultaneously to the end of the string $$$T2+S2$$$, each step they travel one character. If $$$j > i$$$, then $$$q$$$ arrives index $$$2n-1$$$ earlier than $$$p$$$ arrives index $$$4n-1$$$, therefore $$$q$$$ would go into the $$$S$$$ area and lose control.
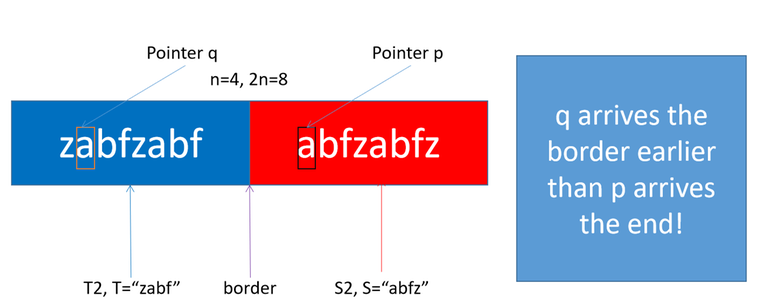
Both $$$S2$$$ and $$$T2$$$ are circular. If $$$S2.substr(i, n) = T2.substr(j, n)$$$, then $$$S2.substr(i, 2n-max(i, j)) = T2.substr(j, 2n-max(i, j))$$$. For example $$$T2=$$$"zabfzabf", $$$S2=$$$"abfzabfz", $$$i=1, j=0, n=4$$$, then $$$2n-max(i, j)=7$$$, "abfzabf"=="abfzabf". When the pointers $$$p, q$$$ are in the area of $$$S2, T2$$$, respectively, they are "safe". The key problem is pointer $$$q$$$ might wander out $$$T2$$$. So we need to protect $$$q$$$ when $$$q$$$ is out $$$T2$$$. A key idea is to add protection. We construct $$$g(T2, S2)$$$ as $$$T2$$$ + string(n-1, 'z') + $$$S2$$$. The string(n-1, 'z') is a safe zone. Since $$$0 \leq i,j \leq n-1$$$, When $$$p$$$ reaches the end of the string, it is guaranteed that $$$q$$$ is in $$$T2$$$ or the safe zone string(n-1, 'z') and $$$SF(g(T2, S2), j) > SF(g(T2, S2), i + 3n-1)$$$. Reason of $$$3n-1$$$: The length of $$$T2$$$ is $$$2n$$$ and the length of the safe zone is $$$n-1$$$. $$$2n + n-1 = 3n-1$$$.
Wrong answer (during contest) without the "safe zone": WA.
Correct answer (after contest, sad, QwQ) with a "safe zone": AC.
Core code:
int main(){
int n;
string s, t;
cin >> n >> s >> t;
string large = t + t + string(n-1, 'z') + s + s;
vector<int> v = move(atcoder::suffix_array(large)); //O(n)
ll ans = 0, snum = 0;
//You can list S-T suffice like S S T S S T T...
//When you meet T, add the number of S before that T to answer.
for(int i = 0; i < 5*n-1; ++i){
int x = v[i];
if(x >= 3*n-1 && x <= 4*n-2){
++snum;
}
if(x >= 0 && x <= n-1){
ans += snum;
}
}
cout << ans << "\n";
}











my man worked so hard only to see his blog being downvoted
Yeah that is a sad story...Actually I end up failing to solve it but I think keeping notes will make progress.
I think you prepare this blog for long.So I support you,thank you!
Thank you! They might think I occupy the "recent action" on purpose.