This is a blog for cp newbies (like me).
For a long time I think the Dijkstra algorithm (dij) only has two usages:
(1) Calculate the distance between vertices when the weights of edges are non-negative.
(2) (Minimax) Given a path $$$p = x_1x_2...x_n$$$, define $$$f(p) := \max_{i=1}^{n-1}d(x_i, x_{i+1})$$$. Given source vertex $$$s$$$ and target vertex $$$t$$$, dij is able to calculate $$$min \{f(p)|p\,\text{is a s-t path}\}$$$.
However, dij works for a function class, not only the sum/max functions. The sum/max functions are only the two most frequently used members of this function class, but the function class is far larger. Once the function $$$f$$$ satisfies several mandatory properties, you could use dij. The word "function class" is like an abstract class in C++:
struct f{
virtual bool induction_property() = 0; //bool: satisfy or not
virtual bool extension_property() = 0; //bool: satisfy or not
virtual bool dp_property() = 0; //bool: satisfy or not
};//dijkstra function.
dij(f);
The graph $$$G=(V(G),E(G))$$$. WLOG we assume $$$G$$$ is connected. There is a non-empty source set $$$S \in V(G)$$$ that needs not be a singleton. A path $$$p$$$ is a vector of vertices $$$\{v_1,v_2,...,v_n\}$$$ and the function $$$f$$$ maps paths to real numbers: $$$\text{path} \rightarrow \mathbb{R}$$$. To be brief, $$$f(\{v_1,v_2,...,v_n\})$$$ is shorten to $$$f(v_1,v_2,...,v_n)$$$. We say that dij works for $$$f$$$ if $$$\forall v \in V(G)$$$, dij correctly computes $$$d(v) := \min f(\{p \mid p\,\text{is a S-v path}\})$$$. $$$f$$$ should satisfy three properties that are also sufficient:
(1, induction base) $$$\forall s \in S,\,f(s)$$$ should be correctly initialized. Pay attention that $$$f(s)$$$ needs not to be $$$0$$$.
(2, Extension property) $$$\forall p$$$, for every vertex $$$v$$$ adjacent to the end of $$$p$$$ (p.back()), $$$f(p \cup v) \geq f(p)$$$.
(3, dynamic programming (dp) property) If path $$$p, q$$$ has the same end (i.e., p.back()==q.back()) and $$$f(p) \geq f(q)$$$, then for every vertex $$$v$$$ adjacent to p.back(), $$$f(p \cup v) \geq f(q \cup v)$$$.
Remarks of the dp property:
First, The dp property guarantees that, if $$$\{v_1, v_2, ..., v_n\}$$$ is the shortest path from $$$v_1$$$ to $$$v_n$$$, then for $$$\forall 1 \leq k \leq n$$$, $$$\{v_1, v_2, ..., v_k\}$$$ is the shortest $$$v_1$$$-$$$v_k$$$ path. You can do induction from end to front.
Second, if $$$f(p) = f(q)$$$, then $$$f(p \cup v) = f(q \cup v)$$$. Because $$$f(p) \geq f(q)$$$, $$$f(p \cup v) \geq f(q \cup v)$$$. Because $$$f(q) \geq f(p)$$$, $$$f(q \cup v) \geq f(p \cup v)$$$. Therefore $$$f(p \cup v) = f(q \cup v)$$$.
The necessity of the induction base is obvious. Otherwise, the $$$f$$$(source vertices) are wrong. For the second property, it is well known that the sum version of dij (shortest path) does not work for edges with negative cost (but the max version works!). For the dp property, let's consider the following example:

In this example $$$f(p):=\sum\limits_{i=1}^{n-1} i \text{dis}(v_i, v_{i+1})$$$. $$$f(ABC) = 1+4*2 = 9$$$; $$$f(AC)=10$$$; $$$f(ABCD) = 1+4*2 + 5*3=24$$$, $$$f(ACD)=10+5*2=20$$$. Since $$$f(ABC) < f(AC),\,f(ABCD) > f(ACD)$$$, $$$f$$$ violates the dp property. In this case, dij does not work, because dij uses ABC to slack D, giving a wrong result $$$24$$$ instead of the correct answer $$$20$$$.
We denote $$$d(v)$$$ as the real value of the shortest path (i.e., $$$\min f(\{p \mid p\,\text{is a S-v path}\}$$$), and $$$h(v)$$$ as the value calculated by dij. We want to prove $$$\forall v \in V(G),\,h(v) = d(v)$$$. We briefly review the outline of the dij:
define a distance array d. Initially fill d with INF;
Initialize d(s), h(s) for all source vertices s in S;
define a set T which is initially S;
constexpr int calculation_limit = |V(G)|; //You can set the calculation limit to an arbitrary number you want, default |V(G)|
int i = 0; //frame number
while T != V(G) && i < calculation_limit{
choose a vertex u that is not in T with the lowest h value; //Choice step
for every vertice v not in T and adjacent to u, update h(v) as h(v) = min(h(v), f([path from S to u] + v)). //You can record the shortest path from S to v here; //Slack step
T.insert(u);
i++;
}
In the induction step, the $$$d$$$ is correctly computed for every source vertex. In the $$$i$$$-th frame, a vertex $$$u$$$ is chosen in the choice step. We assume that for every $$$v$$$ chosen in the choice step of $$$0,\,1,\,2...\,i-1$$$ frames, $$$h(v) = d(v)$$$. For the $$$i$$$-th frame, I am going to show $$$h(u) = d(u)$$$. Consider the shortest path from $$$S$$$ to $$$u$$$ (we call it $$$S-u$$$ path, and it must exist since the graph is finite), and denote $$$y$$$ as the last vertex that does not belong to $$$T$$$:
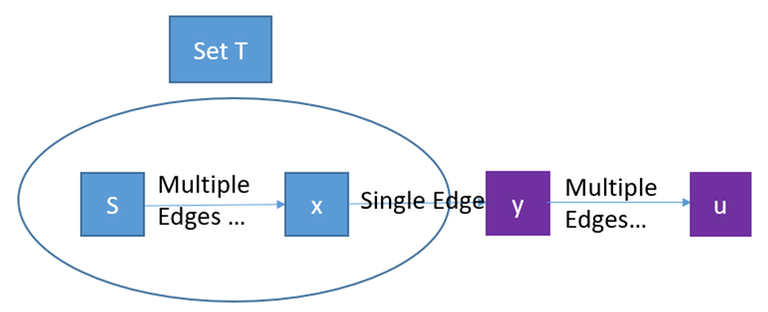
In the following proof, $$$S-x$$$ means a path from S to $$$x$$$. It is not set difference.
First, for all source vertices, i.e., $$$\forall s \in S$$$, we have $$$h(s) = d(s)$$$. That is property 1, induction base.
(1) $$$h(u) \leq h(y)$$$. That is irrelevant to these properties, because dij always choose the vertex $$$u \notin T$$$ with the lowest $$$h$$$ value, if $$$h(u) > h(y)$$$, dij will not choose $$$u$$$ in this frame.
(2) $$$d(y) \leq d(u)$$$. This uses the extension property. $$$S-u$$$ path is shortest, so $$$f(S-u)=d(u)$$$. Due to the extension property, $$$f(S-y) \leq f(S-u)$$$. Since $$$d(y) = \min \text{all}\,f(S-y)\,\text{paths}$$$, we get $$$d(y) \leq d(u)$$$.
(3) $$$h(y) \leq f(S-x-y)$$$. This uses the dp property. By the induction hypothesis, $$$y$$$ is slacked using some path $$$p$$$ from S to x. Please be careful, $$$p$$$ needs not to be the $$$S-x$$$ path in the above picture. But according to the first remark of the dp property, $$$f(S-x) = f(p) = d(x)$$$. Therefore, by the second remark of the dp property, $$$y$$$ is slacked by $$$f(p-y) = f(S-x-y)$$$. When calculating $$$f(p-y)$$$, the algorithm actually uses $$$h(x)$$$ instead of $$$f(p)$$$, by the induction hypothesis, $$$h(x)$$$ is correctly computed, equals to $$$f(p)$$$.
(4) $$$d(y) = f(S-x-y)$$$. This uses the dp property (the first remark).
(5) $$$h(y) = d(y)$$$. $$$h(y)$$$ gives a feasible path from $$$S$$$ to $$$y$$$, which is greater or equal than the shortest path $$$d(y)$$$, that is $$$h(y) \geq d(y)$$$. By (3, 4) $$$h(y) \leq d(y)$$$. Therefore $$$h(y) = d(y)$$$.
(6) $$$h(u) = d(u)$$$. $$$h(u) \leq h(y) = d(y) \leq d(u) \leq h(u)$$$. Therefore $$$h(u) = d(u)$$$.
Now I offer three examples of elegant usage of the function class.
Example 1:
Leetcode2386: Find the K-Sum of an Array. I failed to solve it during the contest. The problem is: You are given an integer array nums and a positive integer k. You can choose any subsequence of the array and sum all of its elements together. We define the K-Sum of the array as the kth largest subsequence sum that can be obtained (not necessarily distinct). Return the K-Sum of the array. For example:
Input: nums = [2,4,-2], k = 5
Output: 2
Explanation: All the possible subsequence sums that we can obtain are the following sorted in decreasing order: 6, 4, 4, 2, 2, 0, 0, -2. The 5-Sum of the array is 2.
n := len(nums) <= 100000; k <= min(2000, 1 << n)
First, we are calculating the "largest", so we need to change $$$\leq$$$ to $$$\geq$$$ in the three properties. We first add all nonnegative elements in nums. The sum of nonnegative elements is the source vertex that is calculated correctly (property 1). We denote the sum as $$$S$$$. For example, if $$$nums=[2, 4, -2],\,S = 6$$$. We set every $$$nums[i]$$$ to $$$-nums[i]$$$ if $$$nums[i] < 0$$$. After this statement, all $$$nums[i] \geq 0$$$. Then, we sort nums ascendingly. For example, nums: $$$[2, 4, -2] \rightarrow [2, 4, 2] \rightarrow [2, 2, 4]$$$. We define the graph $$$G$$$ as follows: The vertex $$$v \in [0, 2^n-1]$$$ is a binary string of length $$$n$$$. If $$$v[i]=1$$$, keep $$$nums[i]$$$, otherwise, if $$$v[i]=0$$$, discard $$$nums[i]$$$. For each vertex the out degree is at most $$$2$$$: (1)Set $$$v[i]$$$ to $$$0$$$. (2) If $$$i \geq 1$$$, Set $$$v[i]$$$ to $$$0$$$ and recover $$$v[i-1]$$$ to $$$1$$$. Below is the search tree:
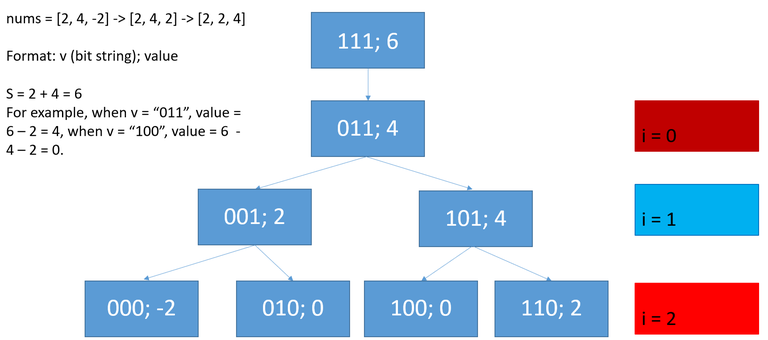
First, the graph $$$G$$$ is a connected tree. It is left to you as an exercise. Feel free to comment if you disagree with it. For a vertex $$$v$$$, let $$$f(v) := S - \sum\limits_{i=0}^{n-1}(1 - v[i]) * nums[i]$$$ ($$$f(v)$$$ is well-defined, there is only one path from root to $$$v$$$). You can verify that $$$f$$$ satisfies the extension property (That is why we need to sort nums), and due to the nature of add, it satisfies the dp property. Even when the abstracted graph is super large, If the degree of each vertex (which decides how many adjacent vertices we need to explore, in this problem, 2) and the calculation_limit is small enough (In this problem, $$$\leq 2000$$$), the dij is feasible even if the abstracted graph is super large, remember to use a priority queue! Below is the code written by 0x3f:
//Original code address: https://leetcode.cn/problems/find-the-k-sum-of-an-array/solution/zhuan-huan-dui-by-endlesscheng-8yiq/
class Solution {
public:
long long kSum(vector<int> &nums, int k) {
long sum = 0L;
for (int &x : nums)
if (x >= 0) sum += x;
else x = -x;
sort(nums.begin(), nums.end());
priority_queue<pair<long, int>> pq;
pq.emplace(sum, 0);
while (--k) {
auto[sum, i] = pq.top();
pq.pop();
if (i < nums.size()) {
pq.emplace(sum - nums[i], i + 1); //Discard nums[i-1]
if (i) pq.emplace(sum - nums[i] + nums[i - 1], i + 1); //Keeps nums[i-1]
}
}
return pq.top().first;
}
};
Example 2:
ABC267E Erasing Vertices 2. Left as practice.
Example 3
ARC150C Path and Subsequence. This problem is super interesting, editorial: https://atcoder.jp/contests/arc150/editorial/4999. There are two sequences $$$A$$$ and $$$B$$$, and an undirected connected graph $$$G=(V(G), E(G))$$$. The problem asks: For every simple path from vertex $$$1$$$ to vertex $$$N$$$, $$$p = (v_1, v_2, ..., v_k);\,v_1=1,\;v_k=N$$$, is $$$B$$$ a (not necessarily contiguous) subsequence of $$$(A_{v_1}, A_{v_2}, ..., A_{v_k})$$$? All sequences are 1-indexed.
For every simple path $$$p$$$ (not necessarily starting from $$$1$$$ and ending at $$$n$$$), we define:
A(p) := list(map(lambda x: A_x, p))
$$$f(p) := \max\{j|[B_1, B_2,...,\,B_j] \text{is a subsequence of}\,A(p)\}$$$.
For example,
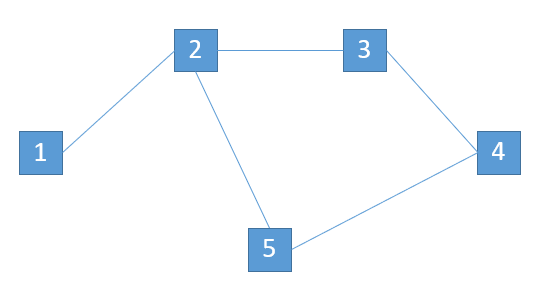
$$$A = [1, 2, 3, 5, 2], B = [1, 3, 2]$$$. If $$$p = [1, 2, 5]$$$, $$$A(p) = [A[1], A[2], A[5]] = [1, 2, 2]$$$, $$$f(p)=1$$$, because only the first $$$1$$$ elements of $$$B$$$ ($$$[1]$$$) is a subsequence of $$$A(p)$$$. If $$$p = [1, 2, 3, 4, 5]$$$, $$$A(p) = [A[1], A[2], A[3], A[4], A[5]] = [1, 2, 3, 5, 2]$$$ and $$$f(p) = 3$$$, because the first $$$3$$$ elements of $$$B$$$ ($$$[1, 3, 2]$$$) is a subsequence of $$$A(p)$$$. Does such $$$f$$$ satisfy the three properties? For the first property, we need to correctly initialize $$$f({1}) := [A[1] = B[1]]$$$. Second, the extension property obviously holds. Third, for the dp property, if $$$p_1 = p + [u]$$$:
Therefore, if $$$p$$$ and $$$q$$$ are simple paths with same the same ending, and $$$f(p) > f(q)$$$, we must have $$$f(p + [u]) \geq f(q + [u])$$$. That is because adding one vertex could increase $$$f(q)$$$ at most $$$1$$$. If $$$f(p) = f(q)$$$, Then $$$f(p + [u]) = f(q + [u])$$$. That is because, whether $$$f(p_1)$$$ ($$$f(q_1)$$$) is $$$f(p)$$$ or $$$f(p)+1$$$ ($$$f(q)$$$ or $$$f(q)+1$$$) depends only on $$$A_u$$$ and $$$B_{f(p)+1}$$$, which are the same for $$$p$$$ and $$$q$$$. Therefore, the dp property holds.
You can solve this problem using dij in $$$O(|V(G)| + |E(G)|)$$$.
--- Update: Fix some typos. I do not intentionally occupy the "Recent actions" column.











Auto comment: topic has been updated by CristianoPenaldo (previous revision, new revision, compare).
Auto comment: topic has been updated by CristianoPenaldo (previous revision, new revision, compare).
Auto comment: topic has been updated by CristianoPenaldo (previous revision, new revision, compare).
For LC2386, if the restriction of k (<= 2000) is removed, then unless P=NP, this problem cannot be solved in P. We can reduce the subset sum problem to it. If LC2386 has an algorithm in P, the subset sum problem could be solved in P using binary search queries. For example the target sum is 8 and n=5. First you compute the 16-sum. If larger than 8, then compute the 24-sum...
Auto comment: topic has been updated by CristianoPenaldo (previous revision, new revision, compare).
The extension property is not needed, we can replace it by assuming that no negative cycles exist.
Nvm, that would be too slow :D
Sorry, would you please elaborate this sentence?
The relaxation step of Dijkstra's algorithm can potentially be wasting time as you are no longer guaranteeing that the smallest element in the queue has the correct distance computed.
I haven't the clue as to understanding this. Could you please list the topics one must know to begin reading this?
Would you please inform me where you are confused, please? I think basic graph theory/data structure knowledge is enough.
confused about the entirety of the blog. It's not that the blog is bad, it's that I'm quite new to CP, so my understanding of things like this is quite dim. That's why I asked for the topics that one must know to begin reading this.
If you have a good understanding of Dijkstra's Algorithm + its proof, then that is probably sufficient to understand it. However, this to me seems like a very formal way of looking at this technique, and I would try to understand the intuition behind why each of these properties is required first.
Can the dijkstra algorithm calculate a minimum path for any cumulative function whose value can only increase or persist while iterating through the path? Say, we want to find a path from one vertex to all other vertex, whose bitwise-or of the weights is minimal. Can we use dijkstra in this context?
Good question. But I do not think so. $$$2 > 1$$$ but $$$2|2 = 2 < 1|2 = 3$$$, the dp property fails.
No, Miku in cup, we would need to iterate through powers of two from large to small. Potentially solvable with O(nlogb) states and 01-bfs? idk